
Indiana University - Purdue University Fort Wayne
Opus: Research & Creativity at IPFW
,2% "12/(,& ,#-,01/2"1(-,,&(,$$/(,&
$"',-*-&5 "2*152!*(" 1(-,0
$. /1+$,1-% ,2% "12/(,& ,#-,01/2"1(-,
,&(,$$/(,&$"',-*-&5
Applied Strength of Materials for Engineering
Technology
Barry Dupen
Indiana University - Purdue University Fort Wayne#2.$,!(.%4$#2
-**-41'(0 ,# ##(1(-, *4-/)0 1 '8.-.20(.%4$#2+"$1(#% ".2!0
/1-%1'$ ..*($#$"' ,("0-++-,0
7(0$#(1(-,' 0!$$,02.$/0$#$#
7(0--)(0!/-2&'11-5-2%-/%/$$ ,#-.$, ""$00!51'$$. /1+$,1-% ,2% "12/(,& ,#-,01/2"1(-,,&(,$$/(,&$"',-*-&5 1.20
$0$ /"'/$ 1(3(15 11' 0!$$, ""$.1$#%-/(,"*20(-,(, ,2% "12/(,& ,#-,01/2"1(-,,&(,$$/(,&$"',-*-&5 "2*152!*(" 1(-,0!5
, 21'-/(6$# #+(,(01/ 1-/-%.20$0$ /"'/$ 1(3(15 1-/+-/$(,%-/+ 1(-,.*$ 0$"-,1 "1 #+(,*(!(.%4$#2
.20(1 1(-,
//52.$, Applied Strength of Materials for Engineering Technology$#2/#2$,(3$/0(15
'8.-.20(.%4$#2+"$1(#% ".2!0

Barry Dupen
Associate Professor, Mechanical Engineering Technology, Indiana University – Purdue University Fort Wayne
v.10 Revised August 2016. This work is licensed under Creative Commons Attribution-ShareAlike 4.0
International (CC BY-SA 4.0) See creativecommons.org for license details.
1
Preface...............................................................................................3
Purpose of the Book....................................................................3
Editors.........................................................................................4
Cover Photos...............................................................................5
Terminology......................................................................................6
Definitions.........................................................................................9
Chapter 1: Introduction to Strength of Materials...........................11
What is Strength of Materials?.................................................11
The Factor-Label Method of Unit Conversion........................12
Chapter 2: Stress and Strain............................................................17
Normal Stress and Strain..........................................................17
Sign Convention.......................................................................19
Shear Stress and Strain.............................................................20
Chapter 3: Poisson's Ratio and Thermal Expansion......................23
Poisson's Ratio..........................................................................23
Thermal Expansion and Thermal Stress..................................25
Chapter 4: Pressure Vessels and Stress Concentrations................28
Thin-Walled Pressure Vessels..................................................28
Stress Concentration in Tension...............................................30
Chapter 5: Bolted and Welded Joints.............................................33
Bolted Lap Joints Loaded in Tension......................................33
Welded Lap Joints....................................................................38
Chapter 6: Properties of Areas........................................................41
Dimensions and Area................................................................41
Centroid and Centroidal Axes..................................................41
Moment of Inertia of a Rectangle............................................41
Compound Beams Sharing a Centroidal Axis.........................42
Hollow Beams Sharing a Centroidal Axis...............................43
The Transfer Formula...............................................................44
Compound Beams With Different Neutral Axes.....................45
Hollow Beams With Different Neutral Axes...........................48
Moment of Inertia about the y-y Neutral Axis........................51
Shortcuts....................................................................................54
Radius of Gyration....................................................................54
Polar Moment of Inertia...........................................................54
Chapter 7: Torsion in Round Shafts...............................................55
Shear Stress in a Round Shaft..................................................55
Angle of Twist in a Round Shaft..............................................57
Stress Concentration in Torsion...............................................58
Chapter 8: Beam Reactions, Shear Diagrams, and Moment
Diagrams..........................................................................................60
Loads on Beams........................................................................60
Reactions for Simply-Supported Simple Beams.....................61
Reactions for Overhanging and Cantilever Beams..................64
Shear Diagrams.........................................................................66
Moment Diagrams....................................................................72
Chapter 9: Stresses in Beams..........................................................82
Bending Stress in Beams..........................................................82
Bending Stress in Wide-Flange Steel Beams..........................84
Shear Stress in Beams...............................................................87
Allowable Load.........................................................................92
Chapter 10: Beam Deflection.........................................................94
Radius of Curvature..................................................................94
The Formula Method for Simple Cases...................................95
Formula Method Hints..............................................................98
The Formula Method for Complex Cases: Superposition.......98
Visualizing the Deflection Curve...........................................100
Chapter 11: Beam Design.............................................................102
Wide-Flange Steel Beam Design in Six Easy Steps..............102
Timber Beam Design in Six Easy Steps................................108
All Other Beams.....................................................................110
Chapter 12: Combined Stresses....................................................112
Tension + Bending..................................................................112
Bending in Two Directions....................................................112
Eccentric Loading...................................................................114
Chapter 13: Statically Indeterminate Beams................................118
Defining Determinate and Indeterminate Beams..................118
Method of Superposition........................................................118
Chapter 14: Buckling of Columns................................................124
Types of Columns...................................................................124
Ideal Slender Columns...........................................................124
Structural Steel Columns........................................................126
Steel Machine Parts................................................................127
Chapter 15: Visualizing Stress and Strain....................................130
Measuring Stress.....................................................................130
Stress at the Base of a Short Block........................................130
Mohr's Circle...........................................................................131
Bibliography..................................................................................148
Textbooks................................................................................148
Other Reading Material..........................................................148
Appendix A: Units........................................................................149
SI System of Units..................................................................149
US Customary System of Units.............................................149
Appendix B: Materials Properties................................................150
Metals, Concrete, & Stone.....................................................150
Appendix C: Properties of Areas..................................................154
Center of Gravity, Area, Moment of Inertia, and Radius of
Gyration..................................................................................154
Appendix D: Properties of Steel Beams and Pipes......................157
W-beams.................................................................................157
Steel Pipes...............................................................................161
Copper Tubing........................................................................162
Appendix E: Mechanical and Dimensional Properties of Wood.163
Mechanical Properties of Air-Dried Boards and Timber......163
Softwood Lumber and Timber Sizes.....................................164
Appendix F: Beam Equations.......................................................166
Index..............................................................................................171
Index..............................................................................................171
2

Preface
1.9 million bachelors degrees are awarded annually in the US.
1
About 92 thousand are Engineering degrees, and about 17
thousand are Engineering Technology degrees and Technician degrees. The number of Mechanical, Civil, and Construction
Engineering Technology graduates is only about 2 thousand per year, so the market for algebra-based Strength of Materials
textbooks for Engineering Technology is a small fraction of the market for calculus-based Engineering textbooks.
Since I attended college in the 1980s, textbook prices have risen about twice as fast as inflation. The internet did not exist
back then, so all textbooks were printed. Now we have another option: low-cost or free online e-books which are revised
more frequently than printed books. While traditional textbooks are revised every 4 to 10 years based on input from experts
in the topic, this e-book is revised every semester based on input from experts in learning: the students.
Students complain that the explanations in many Engineering Technology textbooks are too theoretical, too wordy, and too
difficult to understand. They also complain about the lack of complete unit conversions in example problems, and
inconsistent use of symbols between related courses. For example, some authors use s
n
, s
s
, and e for normal stress, shear
stress, and strain, instead of the standard Greek symbols σ, τ, and ε. This use of Latin characters with multiple subscripts
confuses students because the Greek symbols are used in other textbooks, and because capital S is used for section modulus
later in the course. Students have trouble distinguishing between s and S on the chalkboard and in their notes.
Professors complain that too many students copy answers from online solution manuals or fraternity homework files instead
of learning to solve problems from scratch, then these students fail exams. Probably 10% of the learning in Strength of
Materials occurs in class, and 90% occurs as students solve problems. Deliberately, the problem set for this book is not
available online, and is changed every semester.
I teach Strength of Materials to Mechanical and Construction Engineering Technology students. These students tell me they
want help with algebra skills, unit conversions, and problem-solving approaches. The problem set that accompanies this
book contains problems requiring an algebraic answer as well as traditional problems requiring a numerical answer. The
Factor-Label Method of Unit Conversion is emphasized from the first chapter, and is used in all example problems.
Summarizing, the goals of this book are:
• Free distribution over the internet
• Frequent revisions based on student input
• Concise explanations
• Examples with complete unit conversions
• Standard Greek symbols for stress and strain
• Problems requiring algebraic answers as well as problems requiring numerical answers
• Problems requiring answers in sentences to show reasoning and understanding of the topics
This e-book is revised on an ongoing basis. Please send suggestions for improvement to me at [email protected].
Barry Dupen
Indiana University – Purdue University Fort Wayne
Fort Wayne, Indiana
August, 2016
1 Data from 2013-2014. Current numbers are in the Digest of Educational Statistics, published by the National Center for Educational
Statistics, U.S. Department of Education, at nces.ed.gov.
3
Preface
These IPFW students edited the text and contributed to improving this book:
Jacob Ainsworth
Aaron Alexander
George Allwein
Matthew Amberg
Jared Archer
Mark Archer
Mark Armstrong
Justin Arnold
Stuart Aspy
Caleb Averill
Alex Baer
Trenton Barnett
Ryan Baughman
Jacob Beard
Neil Beauchot
Mitchell Bellam
Aaron Bender
Emily Bendix
Maverick Birch
Kevin Black
John Blankenship
Connor Bleke
Jason Bobay
Tyler Bolinger
Daniel Bone
Crystal Boyd
Valerie Bratten
Aaron Bryant
Brady Bryant
Gregory Bunn
Nicholas Burchell
Justin Byerley
Blake Cain
Danny Calderon
Brody Callaghan
Esperanza Castillo
Richard Chadwick
Tyler Chambers
Brian Chaney
Jacob Clasen
Zachary Clevenger
Ryan Clingenpeel
Mitchell Comparet
Uriel Contreras
Jordan Cook
Logan Counterman
Stephen Cox
Dillon Craig
Chad Crosby
Daniel Cummings
Tayler Cummings
Brian Daley
Christopher Davis
Patrick Davis
Ross Dillion
Joshua Dunlap
Jared Elliott
Stephen England
Cameron Eyman
Jacob Falk
Joshua Farlee
Christopher Faurote
Tyler Faylor
Austin Fearnow
Benjamin Fiechter
Alexander Fisher
John Fisher
Misael Flores
Charles Foreman
Bryce Forrester
Camden Fox
Dominick Franco
Michael Friddle
Nathan Frye
Jacob Gaerte
Brett Gagnon
Joseph Gallmeyer
Matthew Gamble
Carl Garringer
Shane Giddens
Andrew Gordon
Almario Greene
Michael Gresley
Ryan Guiff
Lucas Hahn
David Halpin
Charles Hanes
Adam Hanford
Christian Harmeyer
Brian Harper
James Harris
Skyler Hayes
Matthew Hauter
Alexander Heine
Cody Hepler
Cameron Herring
Ben Hinora
Kaleb Herrick
Spencer Hille
Tyler Hinora
Frank Hoffman
James Hoppes
Bradley Horn
Derick Hostetler
Josef Ifer
Sujinda Jaisa-Ard
Ariana Jarvis
Daniel Johns
Jason Joyner
Lucas Kaiser
John Keene
Adam Kelling
Adam Kennedy
Joseph Kent
Hannah Kiningham
Nate Kipfer
Patrick Kirk
Andrew Kitrush
Rachael Klopfenstein
Joel Kumfer
Branden Lagassie
Kyle Lagemann
Doug Lambert
Brandon Lane
Justin Lantz
Taylor Lantz
Patrick Laroy
Venus Lee
Christopher Leek
Daniel Lewis
Jonathan Lewis
Park Lickliter
Eric Liles
Joseph Lortie
Andrew Loughborough
Jonah Mack
Kyle Macke
Cullan Magnuson
Linda Manduka
Austin Mann
Dalton Mann
David MarcAurele
Lucas Martin
Sterling Martin
Alex Mason
La Keisha Mason
Jason Mayes
Jacob Mazurek
Joel McBain
Adam McCarty
Tori McGairk
Michael McLinden
Riley McMurray
James McVicker
Angela Mendoza
Jedd Minnich
Kaitlin Moore
Derek Morreale
Senaid Mrzljak
Travis Mullendore
Blake Nicol
Kyle Noll
Michael Nusbaum
Mitchell Olney
Jordan Owens
Jason Pace
Ryan Pearce
Jacob Penland
Nicholas Penrod
Luis Perea
Tad Pfefferkorn
John Pham
Clayton Philips
John Pogue
Gabe Powell
Braxton Powers
Nathan Pratt
Trey Proper
Dakota Rassman
Justin Reese
James Reitz
Matthew Rejak
James Rensberger
Shawn Reuille
Daniel Reynolds
Daniel Rieman
Charles Rinehart
Jason Ringer
Derek Ripley
Matthew Roell
Jennifer Royer
Connor Ruby
Brandon Rude
Austin Rumsey
Billie Saalfrank
Zachary Saylor
John Schafer
Zackory Schaefer
Riley Schuette
Zeke Schultz
Justin Self
Ryan Sellers
Philip Sheets
Nathan Sheneman
Keith Shepherd
Scott Shifflett
Brad Shamo
Matthew Shimko
Kenneth Short
Trenton Shrock
George Siddons
Travis Singletary
Eric Shorten
Shane Slone
Jacob Smarker
Ellen Smith
Matthew Somerlott
Joshua Sorge
Matthew Steiner
Jason Strole
Jonas Susaraba
Troy Sutterfield
Robert Swanson
Christopher Swygart
Kyle Tew
Zach Thorn
Nathaniel Timmons
Jason Tonner
Chandler Tracey
Cody Turner
James Upton
Jason Vachon
Thadius Vesey
Dakota Vogel
Scott Vorndran
Charles Wadsworth
Jay Wehrle
Travis Weigold
Sam Weisser
Brock Westergaard
Grant Wilson
Kenneth Win
Scott Wolfe
Michael Woodcock
Lyndsay Wright
Matthew Young
Tang Zhong
Additional editing suggestions were provided by Neil Petroff, Visiting Assistant Professor at Purdue University South
Bend; Israr Ahmad of Dammam, Saudi Arabia; and Dr. Parviz Ghavami of Harlingen, Texas.
4
Preface
Cover photos by the author. Geodesic greenhouses at The Eden Project, Bodelva, England (2000); barn ceiling at Somerset
Rural Life Museum, Glastonbury, England (14
th
century); interior of a tourist kiosk near Squamish, British Columbia; 8
mile long Confederation Bridge between New Brunswick and Prince Edward Island (1997); interior of Fitch's covered
bridge, Delhi, New York (1870); Menai suspenion bridge, Menai Bridge, Wales (1826).
This book was created with the Apache Software Foundation's Open Office software v. 4.1.2
5
Terminology
Because the Roman and Greek alphabets contain a finite number of letters, symbols are recycled and used for more than one
term. Check the context of the equation to figure out what the unit means in that equation.
Other science and engineering disciplines use different symbols for common terms. For example, P is used for point load
here; in Physics classes, F is commonly used for point load. Some older Strength of Materials texts use µ for Poisson's ratio,
s for stress, and e for strain; the formulas are the same, but the labels differ.
α
Thermal expansion coefficient °F
-1
°C
-1
γ
Shear strain
⋯
⋯
γ
Specific weight lb./in.
3
, lb./ft.
3
N/m
3
δ
Change in dimension (length, diameter, etc.) in. mm
Δ
Change
⋯
⋯
Δ
Beam deflection in. mm
ε
Strain
⋯
⋯
η
joint
Joint efficiency % %
ν
Poisson's ratio
⋯
⋯
ρ
Density slug/ft.
3
kg/m
3
σ
Normal (perpendicular) stress psi, ksi MPa
τ
Shear (parallel) stress psi, ksi MPa
θ
Angle of twist (radians) (radians)
A , a
Area in.
2
mm
2
, m
2
A'
Term in the General Shear Formula in.
2
mm
2
, m
2
b
Base dimension of a rectangle in. mm
c
Torsion problem: distance from centroid to outer surface
Beam problem: distance from neutral axis to outer surface
in. mm
d
Diameter in. mm
d
Transfer distance in. mm
d
i
, d
o
Inside and outside diameters of a pipe in. mm
d
H
Hole diameter in. mm
e
Eccentricity in. mm
E
Young's modulus (a.k.a. modulus of elasticity) psi, ksi MPa
F.S. Factor of safety
⋯
⋯
G
Shear modulus (a.k.a. modulus of rigidity) psi, ksi MPa
h
Height dimension of a rectangle in. mm
h
Fillet weld throat in. mm
I
Moment of inertia in.
4
mm
4
J
Polar moment of inertia in.
4
mm
4
K
Stress concentration factor
⋯
⋯
K
Effective length factor (in column analysis)
⋯
⋯
l
Fillet weld leg in. mm
L
Length (of a tension member or a beam) ft. m
L
Total weld length in. cm
M
Moment
lb.⋅ft., kip⋅ft.
kN⋅m
6

Terminology
!
n
Number of shear planes
⋯
⋯
N
Number of bolts
⋯
⋯
N
F
Number of holes in the fracture plane
⋯
⋯
p
Fluid pressure psi, ksi kPa
P
Point load lb., kip kN
P
cr
Euler critical buckling load lb., kip kN
P
G
Bolt load – gross tensile failure of the plate lb., kip kN
P
N
Bolt load – net tensile failure of the plate lb., kip kN
P
P
Bolt load – bearing failure of the plate lb., kip kN
P
S
Bolt load – bolt shear failure lb., kip kN
P
weld
Weld load (lapped plates loaded in tension) lb., kip kN
Q
Term in the General Shear Formula in.
3
mm
3
r
Radius (of a hole, fillet, or groove) in. mm
r
G
Radius of gyration in. mm
R
Reaction force lb., kip kN
R
Radius of curvature in., ft. mm, m
S
Section modulus in.
3
mm
3
t
Thickness in. mm
T
Torque
lb.⋅ft., kip⋅ft.
kN⋅m
T
Temperature °F °C
V
Shear load lb., kip kN
w
Distributed load (weight per unit length) lb./ft., kip/ft. kN/m
W
Weight lb., kip kN
x, y, z
Axes in three-dimensional space: x is horizontal, y is vertical,
and z is into the page.
⋯
⋯
x
Distance along the x-axis in., ft. mm, m
y
Distance along the y-axis, such as the distance from the
neutral axis in beam problems
in., ft. mm, m
y
Distance from the reference axis to the x-x axis of a
composite shape [moment of inertia problems]
in. mm
y
Term in the General Shear Formula in. mm
z
Distance along the z-axis in., ft. mm, m
Z
Plastic section modulus in.
3
mm
3
7
Terminology
"# $ "# $
A
α
Alpha
Ν
ν
Nu
B
β
Beta
Ξ
ξ
Xi
Γ
γ
Gamma O
ο
Omicron
Δ
δ
Delta
Π
π
Pi
E
ε
Epsilon P
ρ
Rho
Z
ζ
Zeta
Σ
σ
Sigma
H
η
Eta T
τ
Tau
Θ
θ
Theta Y
υ
Upsilon
I
ι
Iota
Φ
ϕ
Phi
K
κ
Kappa X
χ
Chi
Λ
λ
Lambda
Ψ
ψ
Psi
M
μ
Mu
Ω
ω
Omega
8
Definitions
!
Allowable (stress, load, etc.)..............Permitted for safe design.
Bending moment,
M
........................Moment in a beam that is loaded in bending with transverse loads.
Bending stress,
σ
..............................A normal stress along the length of a beam that develops due to transverse loading.
Buckling.............................................Collapse of a long, thin member under longitudinal compressive loading, at a load
much lower than the load that causes yielding in tension.
Density,
ρ
.........................................Mass density is the mass of an object or fluid divided by its volume. See specific
weight entry for weight density.
Distributed load,
w
...........................Force acting over a length (such as the weight of a beam) or area (such as a snow load
on a roof). Compare point load.
Eccentricity,
e
...................................Distance between the neutral axis of a part and the location of an applied point load.
Effective length of a column..............Portion of the length of a column that bows like a fully pinned column.
Elastic deformation.............................Temporary deformation; release the load and the part returns to its original shape.
Compare plastic deformation.
Elastic modulus,
E
...........................A measure of the stiffness of a material (the resistance to elastically deforming under
a given load.) The slope of the linear elastic portion of the stress-strain curve. Also
called Young's modulus or modulus of elasticity.
Euler critical buckling load,
P
cr
.......The load at which an ideal Euler column will fail, assuming perfect material and
perfectly aligned loading.
Factor of Safety, F.S...........................The material's strength (typically yield strength) divided by the actual stress in the
part. Also called “factor of ignorance” because it includes unknowns such as
materials defects, improper installation, abuse by the operator, lack of maintenance,
corrosion or rot, temperature variations, etc.
Fillet weld...........................................A weld with a triangular cross section used for joining lapped plates. Unlike soldering
or brazing, welding involves melting the base metal as well as the joining material.
Fracture plane.....................................In a bolted joint that fails, fracture occurs through the bolt holes or through a plate
away from the bolt holes...the site of fracture is called the fracture plane.
General shear formula........................Equation for finding the shear stress within a beam of any shape.
Joint efficiency...................................The efficiency of a bolted or welded joint is the lowest allowable load divided by the
allowable load of the weaker of the two plates some distance from the joint.
Longitudinal direction........................Along the length of a part, such as a beam or shaft. Compare transverse direction.
Longitudinal (axial) stress,
σ
...........Normal stress that develops in a tensile or compressive member due to axial loading.
Modulus of elasticity,
E
...................See elastic modulus.
Moment,
M
.......................................More accurately called a force moment, the product of a length and a transversely
applied force. Used in beam problems. There are other types of moment (such as area
moment: the product of a length and an area).
Moment of inertia,
I
.........................More accurately called “second moment of area”. Divide a shape into n tiny areas a,
each at a distance y from the x-x centroidal axis, and sum the areas and distances as
I
x
=
∑
1
n
a
i
y
i
2
. The larger the moment of inertia, the greater the bending load a beam
can support, and the less bending deflection will occur.
Normal................................................Perpendicular, in the mathematical sense.
Normal stress,
σ
...............................Force divided by area, when the force acts perpendicular to the area. Tensile and
compressive stresses are normal stresses.
Plastic deformation.............................Permanent deformation; release the load and the part remains distorted. Compare
elastic deformation.
Plastic section modulus,
Z
................Sum of the first moments of areas above and below the neutral axis of a steel beam.
Used for calculating bending stresses in structural steel beams.
Point load,
P
.....................................Force acting at a single point. Compare distributed load.
Poisson's ratio,
ν
..............................A mechanical property of engineering materials equal to the negative of the transverse
strain divided by longitudinal strain. A measure of how much a tensile member will
thin during elastic deformation.
9

Definitions
Polar moment of inertia,
J
................More accurately called “polar second moment of area”. Divide a shape into n tiny
areas a, each at a distance r from the centroid, and sum the areas and distances as
J =
∑
1
n
a
i
r
i
2
. The larger the polar moment of inertia, the greater the torque a shaft can
support, and the less angular twist will be produced.
Pressure (of a fluid),
p
.....................Fluid equivalent of normal stress. A pressurized gas produces a uniform pressure
perpendicular to the walls of the pressure vessel. A pressurized liquid produces a
uniform pressure in a small pressure vessel; the pressure is nonuniform in a tall vessel
due to gravity (lower pressure at the top, higher at the bottom).
Radius of curvature,
R
.....................If a beam segment is bent with a constant bending moment, the segment becomes a
circular arc with a radius of curvature, R.
Radius of gyration,
r
G
......................Concentrate an area at a distance r from the x-x neutral axis. If the moment of inertia
of the original area is the same as for the concentrated area, then r
Gx
is the radius of
gyration about the x-x axis. The larger the radius of gyration, the more resistant a
column is to buckling. Calculate
r
G
=
√
I / A
.
Reaction moment,
M
A
or
M
B
........Moment at reaction point A or B which supports a transversely loaded cantilever
beam.
Reaction force,
R
A
or
R
B
................Forces at reaction points A or B which support a transversely loaded beam.
Section modulus,
S
...........................Moment of inertia divided by the distance from the neutral axis to the surface. The
larger the section modulus, the more resistant a beam is to bending.
Shear modulus,
G
.............................The slope of the linear elastic portion of the shear stress – shear strain curve.
Shear load,
V
....................................Transverse load on a beam.
Shear plane.........................................In a bolted joint with two plates pulling in opposite directions, the shear plane is the
transverse plane within a bolt that lies at the interface of the two plates.
Shear strain,
γ
..................................Shear deflection divided by original unit length
Shear stress,
τ
...................................Force divided area, when the force acts parallel to the area.
Specific weight,
γ
............................Specific weight, a.k.a. weight density, is the weight of an object or fluid divided by its
volume. The symbol, lower case gamma, is also used for shear strain. In this text,
plain gamma means shear strain, while bold gamma means specific weight. See
density entry for mass density.
Strain (normal),
ε
.............................Change in length of a material under normal load divided by initial length.
Stress..................................................See normal stress, shear stress, bending stress, torsional stress, longitudinal stress.
Stress concentration............................A locally high stress due to a sharp discontinuity in shape, such as a hole or notch
with a small radius. While the overall stress in the part may be at a safe level, the
stress at the discontinuity can exceed yield or ultimate strength, causing failure.
Tensile strength,
σ
UTS
.......................Maximum stress on the stress-strain diagram. Beyond this point, the material necks
and soon breaks.
Thermal expansion coefficient,
α
....Materials property that determines how much a material expands or contracts with
changing temperature.
Torque,
T
..........................................Rotational moment applied to a shaft. Units of moment and torque are the same (force
× distance).
Torsion................................................Twisting of a shaft due to an applied torque.
Torsional stress,
τ
............................A shear stress that develops in a shaft due to torsional loading.
Transfer distance,
d
..........................Term used in calculating moment of inertia of a compound shape.
Transverse direction...........................Perpendicular (crosswise) to the length of a long part, such as a beam or shaft.
Compare longitudinal direction.
Ultimate tensile strength,
σ
UTS
.........See tensile strength.
Yield strength,
σ
YS
............................Below the yield strength, a material deforms elastically; above it, the material deforms
plastically (undergoes permanent deformation).
Young's modulus,
E
.........................See elastic modulus.
10

Chapter 1: Introduction to Strength of Materials
%&'
(')
Statics is the study of forces
acting in equilibrium on rigid
bodies. “Bodies” are solid objects,
like steel cables, gear teeth,
timber beams, and axle shafts (no
liquids or gases); “rigid” means
the bodies do not stretch, bend, or
twist; and “equilibrium” means
the rigid bodies are not
accelerating. Most problems in a
Statics textbook also assume the
rigid bodies are stationary. These
assumptions do not match reality
perfectly, but they make the math
much easier. This model is close
enough to reality to be useful for
many practical problems.
In Strength of Materials, we keep
the assumptions of bodies in
equilibrium, but we drop the
“rigid” assumption. Real cables
stretch under tension, real floor
joists bend when you walk across
a wood floor, and real axle shafts
twist under torsional load.
Strength of Materials is a difficult
course because the topics are
cumulative and highly
interconnected. If you miss an
early topic, you will not
understand later topics. This table
lists Strength of Materials topics,
and indicates which chapters use
each topic.
Chapter number
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Algebra & some trigonometry ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●
Factor-label method of unit conversion ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●
Normal stress ● ● ● ● ● ● ● ● ● ●
Normal strain ● ● ●
Yield strength ● ● ● ● ●
Tensile strength ● ● ●
Shear stress ● ● ● ● ● ●
Shear strain ● ●
Young's modulus ● ● ● ● ● ●
Axial deflection ● ●
Poisson's ratio ●
Transverse strain ●
Transverse deflection ● ● ● ●
Strain due to multiaxial loads ●
Thermal expansion ●
Thermal stress ●
Pressure vessels ● ●
Stress concentration ● ●
Joint efficiency ● ●
Bolted joints ●
Welded joints ●
Moment of inertia of a simple shape ● ● ● ● ● ● ●
Moment of inertia of a compound shape ● ●
Polar moment of inertia ● ●
Radius of gyration ● ●
Torque ● ●
Shear modulus ●
Beam reactions ● ● ● ● ●
Shear diagrams ● ● ● ● ●
Moment diagrams ● ● ● ● ●
Deflection diagrams ●
Section modulus ● ● ● ●
Plastic section modulus ● ● ●
Interpolation / Similar triangles ● ● ● ● ●
Combined stresses ●
Eccentric loading ●
Statically indeterminate beams ●
Column buckling ●
Mohr's circle ●
If you want to be successful in a Strength of Materials course, you need the following:
• * . Solve every problem methodically. Make your step-by-step solution easy for the reader (the grader)
to understand, with the final solution at the bottom.
• * Solve every problem algebraically before introducing numbers and units.
• . Use the Factor-Label Method of Unit Conversion, the standard in Engineering and Chemistry. The
convention in Physics is to convert everything into SI units, plug numbers into the equation, and hope the units come out
OK. In engineering and chemistry, we introduce the actual units into the equation, and add the unit conversions at the
end of the equation. The reason is that real objects are dimensioned in more than one unit. For example, in the U.S., steel
beam lengths are in feet, depths are in inches; in Canada, steel beam lengths are in meters, depths are in millimeters.
You might be able to convert inches to feet in your head, but it is easy to make mistakes when the unit is exponential
(converting in.
3
to ft.
3
or mm
4
to m
4)
, so use the Factor-Label Method and avoid simple mistakes.
11

Chapter 1: Introduction to Strength of Materials
• (. If you copy someone else’s homework solutions instead of working them out, you will fail the
exams, and you will have to repeat the course. The only way to learn this material is by practicing. For every hour of
class time, expect to spend at least three hours doing homework. A good estimate is 10% of the learning occurs in the
classroom; 90% of the learning occurs while you are solving the problems. Start the homework the same day as class
(while your memory is fresh), work with other students in study groups, go to the professor’s office hours if you do not
understand something, and turn in every homework assignment on time.
• . It comes in light green or light yellow, with a grid printed on the back. Write on the front only; the
printed grid on the back side helps you align graphics and text. With Engineering Paper, you can sketch beam problems
to scale. The graphical result will tell you if the calculated numbers are in the ballpark.
Strength of Materials is one of the most useful courses in an Engineering Technology education. It is the foundation for
advanced Structures courses in Construction Engineering Technology, and the foundation for Machine Elements in
Mechanical Engineering Technology.
+,"'
In Engineering disciplines, we use the three-step Factor-Label Method of Unit Conversion to solve algebraic problems with
mixed units.
% Write the algebraic equation so the desired quantity is on the left of
the equals sign, and an algebraic expression is on the right of the equals sign.
- Draw a horizontal line on the page, and enter numbers and units
above and below the line according to the algebraic expression.
. Draw a vertical line to show the separation between each unit
conversion, and enter all unit conversions necessary to solve the problem. If
the unit is raised to a power, then the conversion factor and unit must be
raised to that power. Consider memorizing the most common conversion
factors, like the ones at the right. See Appendix A for more unit conversions
and metric prefixes, and Appendix B for materials properties such as
thermal expansion coefficient and Young's modulus. Table B1 gives these
properties in U.S. Customary units, while Table B2 gives them in S.I. units.
The units in the final answer must appear in the equation, and all other units
must cancel.
1ft. = 12 in.
1 m = 100cm = 10
3
mm
1 kip = 10
3
lb.
1 Pa = 1N /m
2
1 N = 1kg⋅m /s
2
Metric prefixes
milli- (m) = 10
−3
centi- (c) = 10
−2
kilo- (k) = 10
3
Mega- (M ) = 10
6
Giga- (G) = 10
9
!"
The area of a rectangle is
A=b⋅h
. Given a base
b=83in.
and a height
h=45 ft.
, calculate the area in
square feet.
% The algebraic equation does not need to be manipulated.
- Draw a horizontal line. Enter 83 in. and 45 ft. in the
numerator.
A=b⋅h=
83in.⋅45 ft.
. We want to eliminate inches to obtain a final result in
square feet. Therefore, put 12 inches in the denominator of
the unit conversion, and 1 ft. in the numerator.
A=b⋅h=
83in.⋅45 ft.
∣
ft.
12in.
=311.25ft.
2
12
b
h

Chapter 1: Introduction to Strength of Materials
!#
Stress is force divided by area. If the stress is 1 N/mm
2
, what is the stress in MPa?
% There is no algebra to solve here because we are converting one unit to another.
- Draw a horizontal line. Enter 1 N in the numerator,
and mm
2
in the denominator.
1 N
mm
2
. A pascal is defined as Pa=N/m
2
, so enter Pa in the
numerator. Instead of writing in N/m
2
the denominator, put
N in the denominator and m
2
in the numerator.
1 N
mm
2
∣
Pa m
2
N
Now enter the unit conversions to eliminate the two area
terms: m
2
and mm
2
. There are 10
3
mm in a meter, so use
parentheses to square the number and the unit.
1 N
mm
2
∣
Pa m
2
N
∣
(10
3
mm)
2
m
2
Finally, 1MPa=10
6
Pa. Put MPa in the numerator and 10
6
Pa
in the denominator. If you write the equation without
numbers, it looks like
N
mm
2
∣
Pa m
2
N
∣
mm
2
m
2
∣
MPa
Pa
. Cross out
duplicate terms, and all terms cancel except for MPa. If you
write the equation without units, it looks like
1
∣
(10
3
)
2
∣
10
6
.
1 N
mm
2
∣
Pa m
2
N
∣
(10
3
mm)
2
m
2
∣
MPa
10
6
Pa
N
mm
2
∣
Pa m
2
N
∣
(mm)
2
m
2
∣
MPa
Pa
Solving the equation with numbers and units, we get
1 N / mm
2
=1 MPa
. This is a useful conversion factor in SI
Strength of Materials problems.
1 N
mm
2
∣
Pa m
2
N
∣
(10
3
mm)
2
m
2
∣
MPa
10
6
Pa
=1 MPa
!$
Deflection due to thermal expansion is
δ=α⋅L⋅Δ T
. The upper-case Greek letter
delta means “change”, so
Δ T
means “change in temperature.” Given a deflection
δ=0.06in.
, a length
L=8ft.
, and a thermal expansion coefficient
α=5×10
−6
in./in.°F
, calculate the change in temperature in degrees Fahrenheit.
% Rewrite the equation algebraically to solve for ΔT.
δ=α⋅L⋅ΔT
→
ΔT =
δ
α L
- Draw a horizontal line. Enter 0.06 in. in the
numerator. Since the units for α are a fraction, enter
5×10
6
in.
in the denominator and
in.°F
in the numerator.
Enter 8 ft. in the denominator.
Δ T =
0.06in. in.°F
5×10
−6
in.
8ft.
. Convert feet to 12 inches so the length units to
cancel, and the result is in °F.
Δ T =
0.06in. °F
5×10
−6
8ft.
∣
ft
12 in.
=125 ° F
13
T
1
L
δ
T
2

Chapter 1: Introduction to Strength of Materials
!%
Stress is force divided by area:
σ=
P
A
. Given a force P = 7000 lb. acting on an area A = 3 ft.
2
, calculate the stress in units
of pounds per square inch (psi).
% The equation does not need to be manipulated.
- Draw a horizontal line. Enter 7000 lb. in the
numerator, and 3 ft.
2
in the denominator.
σ=
P
A
=
7000 lb.
3ft.
2
. The stress is in units of pounds per square foot. There
are 12 inches in a foot, but we need to convert square feet,
so square the number and the unit:
(12 in.)
2
. Square feet
cancel, and the answer is in pounds per square inch, also
written psi.
σ=
P
A
=
7000lb.
3ft.
2
∣
ft.
2
(12 in.)
2
=16.2
lb.
in.
2
=16.2 psi
!&
A tensile bar stretches an amount
δ=
P⋅L
A⋅E
where P is the applied load, L is the length of the bar, A is
the cross-sectional area, and E is Young’s Modulus. The bar has a circular cross section. Given a load of
30 kN, a length of 80 cm, a diameter of 6 mm, and a Young’s Modulus of 207 GPa, calculate the
deflection in mm.
% In math class, the area of a circle is given by
A=π r
2
. In real life, we measure diameter using calipers; it
is much easier to measure a diameter than a radius on most
objects. Convert radius to diameter, and the area equation
becomes more useful. This is a good equation to memorize.
A=π r
2
=π(
d
2
)
2
=
π d
2
4
=
π
4
d
2
Combine the two equations to obtain a single algebraic
equation.
δ=
P⋅L
A⋅E
=
4 P L
π d
2
E
- Draw a horizontal line and enter the numbers and
units.
δ=
4⋅30 kN⋅80cm
π (6 mm)
2
207GPa
. The SI unit of stress or pressure is the pascal, where
Pa=
N
m
2
, so
GPa=
10
9
N
m
2
. Since
1kN=10
3
N
, we can
write
GPa=
10
6
kN
m
2
. Three conversion factors are needed:
one to cancel GPa and kN; a second to cancel mm
2
and m
2
;
and a third to put the final answer in mm.
δ=
4⋅30 kN⋅80 cm
π(6 mm)
2
207GPa
∣
GPa m
2
10
6
kN
∣
(10
3
mm)
2
m
2
∣
10 mm
cm
=4.1 mm
14
P
P
L

Chapter 1: Introduction to Strength of Materials
!'
The weight of a solid object is the specific weight of the material times the volume of the object:
W =γV
. The volume of
a rod, pipe, or bar is the cross-sectional area times the length:
V = A L
. Calculate the weight of a 2 inch diameter, 3 foot
long bar of steel. From Appendix B, the specific weight of steel is 0.284 lb./in.
3
% Combine the two equations to solve for weight:
W =γ A L
. Since the rod is round, the cross-sectional area is
A=
π
4
d
2
, therefore
W =
γ π d
2
L
4
- Draw a horizontal line and enter the numbers and
units.
W =
γ π d
2
L
4
=
0.284 lb.
in.
3
π(2in.)
2
3 ft.
4
. The only unit conversion is feet to inches.
W =
γ π d
2
L
4
=
0.284 lb.
in.
3
π(2 in.)
2
3ft.
4
∣
12 in.
ft.
=32.1lb.
!(
Calculate the weight of a 5 cm diameter, 2 meter long bar of steel. From Appendix B, the density of steel is 7.85 g/cm
3
% Use
W =
γπ d
2
L
4
from Example #6. Specific weight is density times gravity:
γ=ρg
, so
W =
ρg π d
2
L
4
.
- Draw a horizontal line and enter the numbers and
units.
W =
ρg π d
2
L
4
=
7.85g
cm
3
9.81 m
s
2
π(5cm)
2
2 m
4
. The SI unit of weight is the newton:
N=
kg m
s
2
.
Notice the unit “g” for grams and the term “g” for
gravity. In science and engineering, we tend to use roman
type for units, and italic type for variables. Another
example is a block sliding on an inclined plane, where “N”
stands for newtons and “N” stands for normal force.
W =
7.85 g
cm
3
9.81 m
s
2
π(5cm )
2
2 m
4
∣
kg
10
3
g
∣
100cm
m
∣
N s
2
kg m
=302 N
!)
A 50 mm thick wood board is planed to a thickness of 38 mm. Calculate how much material was removed, in percent.
Calculate the percent change by subtracting the initial value from the final value, then dividing by the initial value. This
method works whether you are calculating thickness change, weight change, price change, or any other kind of change.
The word “percent” means “per hundred”, so a result of 0.36 is 36%.
t
f
−t
o
t
o
=
38 mm−50mm
50 mm
=−0.24 or −24%
The minus sign means the value decreased.
15

Chapter 1: Introduction to Strength of Materials
!*
Two pieces of carbon fiber composite are glued together as a lap joint. Shear stress is
τ=
P
A
. If the glue has a shear
strength of 1.2 ksi and the joint is loaded with a shear load
P =1700 lb.
, how much glued surface area is required for a
good bond?
Solve algebraically, and split ksi into
kips
in.
2
. Surface area
A=
P
τ
=
1700 lb. in.
2
1.2 kips
∣
kip
1000 lb.
=1.42in.
2
16

Chapter 2: Stress and Strain
-&
$
The words “stress” and “strain” are used interchangeably in popular culture in a
psychological sense: “I’m feeling stressed” or “I’m under a lot of strain.” In engineering,
these words have specific, technical meanings. If you tie a steel wire to a hook in the
ceiling and hang a weight on the lower end, the wire will stretch. Divide the change in
length by the original length, and you have the strain in the wire. Divide the weight
hanging from the wire by the wire’s cross sectional area, and you have the tensile stress
in the wire. Stress and strain are ratios.
The symbol for tensile stress is σ, the lower case Greek letter sigma. If the weight is 25
lb. and the cross-sectional area of the wire is 0.002 in.
2
, then the stress in the wire is
σ=
W
A
=
25 lb.
0.002 in.
2
=12,700
lb.
in.
2
=12,700 psi
.
The symbol for strain is ε, the lower case Greek letter epsilon. If the original length of the wire
L=40in.
and the change in
length
Δ L=0.017 in.
(also written
δ=0.017 in.
), then strain
ε=
Δ L
L
=
δ
L
=
0.017 in.
40in.
=0.000425
. This is a small number,
so sometimes the strain number is multiplied by 100 and and reported as a percent:
0.000425=0.0425%
. You may also
see strain reported in microstrain:
0.000425×10
6
=425
microstrain. Strain is usually reported as a percent for highly elastic
materials like rubber.
!"
A 6 inch long copper wire is stretched to a total length of 6.05 inches. What is the strain?
The change in anything is the final dimension minus the initial dimension. Here, the change in length is the final
length minus the initial length:
Δ L=L
f
−L
o
=6.05in.−6.0 in.=0.05 in.
. Strain is
ε=
Δ L
L
=
0.05 in.
6.0 in.
=0.0083
.
If we hang a bucket from the wire and gradually fill the bucket with water, the weight will gradually increase along with the
stress and the strain in the wire, until finally the wire breaks. We can plot the stress vs. strain on an x-y scatter graph, and
the result will look like this:
This graph shows the stress-strain behavior of a low-carbon steel. Stress is in units of ksi, or kips per square inch, where
1 kip=10
3
lb.
(1 kilopound). The points to the left of the red dashed line are so close together that they smear into a line.
This straight part of the stress-strain curve is the elastic portion of the curve. If you fill the bucket with only enough water to
17
L
ΔL or δ
W
0.00 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16 0.18 0.20
0
10
20
30
40
50
60
70
Strain
Stress
(ksi)

Chapter 2: Stress and Strain
stretch the wire in the elastic zone, then the wire will return to its original length when you empty the bucket.
We can change the range of the strain axis from 0.0-0.2 to 0.000-0.002, to show the elastic data only:
This graph shows the leftmost 1% of the previous graph. The dashed red line is in the same position on both graphs. Now
the individual data points are visible, and the curve is almost perfectly straight up to a strain of about 0.0018. The straight
line has a slope, called Young’s Modulus,
2
or Elastic Modulus, E. The slope of a straight line is the rise over run, so within
this elastic zone,
E=
σ
ε
. Since strain is unitless, Young’s modulus has the same units as stress. Young’s modulus is a
mechanical property of the material being tested:
30×10
6
psi
or 207 GPa for steels,
10×10
6
psi
or 70 GPa for aluminum
alloys. See Appendix B for materials properties of other materials.
!#
What tensile stress is required to produce a strain of 8×10
-5
in aluminum? Report the answer in MPa.
Aluminum has a Young’s modulus of E = 70 GPa. Rewrite
E=
σ
ε
, solving for stress:
σ= E ε=
8×10
−5
⋅70GPa
∣
10
3
MPa
GPa
=5.6 MPa
This cartoon of a stress-strain curve illustrates the elastic and
plastic zones. If you hang a light weight to the wire hanging
from the ceiling, the wire stretches elastically; remove the
weight and the wire returns to its original length. Apply a
heavier weight to the wire, and the wire will stretch beyond
the elastic limit and begins to plastically
3
deform, which
means it stretches permanently. Remove the weight and the
wire will be a little longer (and a little skinnier) than it was
originally. Hang a sufficiently heavy weight, and the wire
will break.
Two stress values are important in engineering design. The
yield strength, σ
YS
, is the limit of elastic deformation; beyond
this point, the material “yields,” or permanently deforms.
The ultimate tensile strength, σ
UTS
(also called tensile strength, σ
TS
) is the highest stress value on the stress-strain curve. The
rupture strength is the stress at final fracture; this value is not particularly useful, because once the tensile strength is
2 Named for Thomas Young, an English physics professor, who defined it in 1807.
3 Here, the word plastic is used in its 17
th
century sense “capable of being deformed” rather than the 20
th
century definition “polymer.”
18
0.0000 0.0002 0.0004 0.0006 0.0008 0.0010 0.0012 0.0014 0.0016 0.0018 0.0020
0
10
20
30
40
50
60
70
Strain
Stress
(ksi)
elastic
zone
Stress, σ
Strain, ε
Elongation
Yield strength
Rupture
strength
Tensile strength
Young's
Modulus, E
plastic zone
elastic
zone

Chapter 2: Stress and Strain
exceeded, the metal will break soon after. Young’s modulus, E, is the slope of the stress-strain curve before the test
specimen starts to yield. The strain when the test specimen breaks is also called the elongation.
Many manufacturing operations on metals are performed at stress levels between the yield strength and the tensile strength.
Bending a steel wire into a paperclip, deep-drawing sheet metal to make an aluminum can, or rolling steel into wide-flange
structural beams are three processes that permanently deform the metal, so
σ
YS
<σ
Applied
. During each forming operation,
the metal must not be stressed beyond its tensile strength, otherwise it would break, so
σ
YS
<σ
Applied
<σ
UTS
. Manufacturers
need to know the values of yield and tensile strength in order to stay within these limits.
After they are sold or installed, most manufactured products and civil engineering structures are used below the yield
strength, in the elastic zone.
4
In this Strength of Materials course, almost all of the problems are elastic, so there is a linear
relationship between stress and strain.
Take an aluminum rod of length L, cross-sectional area A, and pull on it with a load P.
The rod will lengthen an amount δ. We can calculate δ in three separate equations, or
we can use algebra to find a simple equation to calculate δ directly. Young’s modulus
is defined as
E=
σ
ε
. Substitute the definition of stress,
σ=
P
A
, and
E=
σ
ε
=
P
A⋅ε
.
Substitute the definition of strain,
ε=
δ
L
, and
E=
P
A⋅ε
=
PL
Aδ
. Rewrite this equation
to solve for deflection:
δ=
PL
AE
. Now we have a direct equation for calculating the
change in length of the rod.
!$
A 6 foot long aluminum rod has a cross-sectional area of 0.08 in.
2
. How much does the rod stretch under an axial tensile
load of 400 lb.? Report the answer in inches.
Aluminum has a Young’s modulus of
E=10×10
6
psi
.
Deflection
δ=
PL
AE
=
400lb. 6ft.
0.08 in.
2
in.
2
10×10
6
lb.
∣
12in.
ft.
=0.036 in.
$ Young's modulus is in units of psi, but when you write it in an equation, split up the lb. and the in.
2
between
numerator and denominator to avoid unit confusion.
A load that pulls is called a tensile load. If the load pushes, we call it a compressive load. The equations are the same:
compressive stress
σ=P / A
, compressive strain
ε=δ/ L
, and compressive deflection
δ=PL/ AE
. We need a way to
differentiate between compression and tension, so we use a sign convention. Tensile loads and stresses are positive;
compressive loads and stresses are negative. Increases in length are positive; decreases in length are negative.
4 One exception is the crumple zones in a car. During an auto accident, the hood and other sheet metal components yield, preventing
damage to the driver and passengers. Another exception is a shear pin in a snow blower. If a chunk of ice jams the blades, the shear
pin exceeds its ultimate strength and breaks, protecting the drivetrain by working as a mechanical fuse.
19
P
P
A
L L+δ

Chapter 2: Stress and Strain
!%
A 70 kN compressive load is applied to a 5 cm diameter, 3 cm tall, steel cylinder. Calculate stress, strain, and
deflection.
The load is –70 kN, so the stress is .
σ=
P
A
=
4P
π d
2
=
4(−70 kN)
π(5cm )
2
∣
MPa m
2
10
3
kN
∣
(100 cm)
2
m
2
=−35.6 MPa
The negative sign tells us the stress is compressive. Young's modulus
E=
σ
ε
. Rewrite the equation to solve
for strain:
ε=
σ
E
=
−35.6 MPa
207GPa
∣
GPa
10
3
MPa
=−0.000172
Strain is defined as
ε=
δ
L
. Rewrite to solve for deflection:
δ=ε L=
−0.000172⋅3 cm
∣
10 mm
cm
=−0.0052 mm
. The
negative signs tell us that the cylinder is shrinking along the direction of the load.
The stress in the previous examples is called “normal stress” because the stress acts on an area
that is normal, or perpendicular, to the direction of the applied load. Imagine a tall stack of coins
glued together on their faces. If you pull on the ends of the stack, the glue will experience a
stress that is normal (perpendicular) to the face of each coin. If the glue is thick and tacky,
maybe it will tend to stretch, and you can see the coins gradually pull apart along the direction of
the applied load. If the load is 100 lb. and the face area of each coin is 1 in.
2
, then the normal
stress is 100 psi.
Next, imagine taking two coins that are glued together on their faces, and try to slide them apart.
Now the stress is acting parallel to the glue instead of perpendicular to it. This stress is called
shear stress, symbolized by the lower case Greek letter tau, τ. The units are the same as for
normal stress because shear stress is also force divided by area. If the load is 25 lb. and the face
area of each coin is 1 in.
2
, then the shear stress is 25 psi.
Sheet metal joints are often manufactured this way, with adhesive bonding
two lapped sheets to form a lap joint. The load is parallel to the area under
stress (the adhesive in the shear plane between the two lapped panels). Joints
can be designed to put the adhesive in either tension or in shear; typically,
the shear strength of an adhesive is not the same as the strength in tension.
For example, cyanoacrylate adhesive (“superglue”) is stronger in tension than in shear. An adhesive lap joint will fail when
the shear strength of the adhesive is exceeded.
If the sheet metal is held together with rivets instead of glue, then
each rivet is loaded in shear across its cross-section. The shear
plane passes through the rivet where the two sheets meet. In a
bolted joint, use a bolt with a smooth shank instead of a bolt that
is threaded along its entire length. This way, the shear plane can
pass through the smooth shank, which has a larger cross-
sectional area than the root of a thread, and therefore can handle a higher applied load. Later in the book, we will see that
the thread root also acts as a stress concentration site – yet another reason for keeping threads out of shear planes.
20
P
P
P
P
P
P
P
P
P
P
shear
plane

Chapter 2: Stress and Strain
One way to produce holes in sheet metal is by punching them out with a punch and die set. The punch shears the sheet
metal, so we can use shear stress calculations to figure out the stress in the sheet metal,
τ=
P
A
. Here, P is the force of the
punch and A is the sheared area (the perimeter of the shape that is punched times the thickness of the sheet metal t).
!&
A 3 mm thick aluminum sheet is cut with a 4 cm diameter round
punch. If the punch exerts a force of 6 kN, what is the shear stress in
the sheet? Report the answer in MPa.
The punch will create a round slug, where the cut edge is
around the circumference of the slug. Think of the cut edge as the wall
of a cylinder with a height of 3 mm and a diameter of 4 cm. The area
equals the circumference of the circle times the thickness of the sheet
metal:
A=π dt
.
Shear stress
τ=
P
A
=
P
π dt
=
6kN
π⋅4 cm⋅3 mm
∣
MPa m
2
10
3
kN
∣
100 cm
m
∣
10
3
mm
m
=15.9 MPa
A process engineer in a stamping plant will rewrite this equation to solve for P in order to find out whether a press is
capable of punching out blanks of a given size in a sheet metal of known shear strength.
Shear stress controls the design of torsion members. Think of a
round shaft as a series of disks glued together on their faces. If
you twist the shaft with a torque T, the glue will be loaded in
shear because the load is parallel to the face of each disk.
Consider a rectangular block loaded in shear. The block will distort as a
parallelogram, so the top edge moves an amount δ. Divide the distortion by
length L perpendicular to the distortion, and you have the shear strain,
γ=
δ
L
. Like normal strain, shear strain is unitless. Consider the angle
formed between the initial and loaded positions of the block. From
trigonometry, we know that
tan ϕ=
δ
L
.The amount of strain in the cartoon
is exaggerated. For metals, concrete, wood, and most polymers, angle
ϕ
is so small that
tan ϕ≈ϕ
if we measure the angle
in radians, therefore
ϕ≈γ=
δ
L
.
21
P
δ
L
ϕ
punch
P
d
t
slug
TT

Chapter 2: Stress and Strain
+,
Normal stress in a tensile or compressive member is the load divided by the cross-sectional area:
σ=
P
A
Normal strain is the change in length parallel to the load divided by initial length:
ε=
Δ L
L
=
δ
L
Young's modulus is the ratio of stress over strain within the elastic zone of the stress-strain diagram:
E=
σ
ε
The change in length of a tensile or compressive member is derived from the three previous equations:
δ=
PL
AE
Shear stress is the load divided by the area parallel to the load:
τ=
P
A
Shear strain is the deformation parallel to the load divided by initial length perpendicular to the load:
γ=
δ
L
.
22

Chapter 3: Poisson's Ratio and Thermal Expansion
.&/01
/0
Stretch a thick rubber band, and you notice the material gets thinner as it gets longer. This effect
occurs in metals, plastics, concrete, and many other materials. We can predict how much the
thickness changes with a materials property called Poisson’s ratio,
5
which relates the strain along the
tensile axis with the strain in the transverse (crosswise) direction. The symbol for Poisson’s ratio is ν,
the lower case Greek letter nu, which looks similar to the lower case Roman letter v. Poisson’s ratio
is
ν=
−ε
transverse
ε
long
, where
ε
transverse
is the strain in the transverse (crosswise) direction, and
ε
long
is
the strain along the longitudinal axis (also called
ε
axial
). The sign convention for strain is positive for
expansion, negative for shrinkage. Poisson’s ratio is 0.25 for steel, 0.33 for aluminum, and 0.10 to
0.20 for concrete. We can calculate the change in length of a rod by taking the definition of strain,
ε
long
=
δ
long
L
, and rewriting it as
δ
long
=ε
long
L
. In the same way, we can calculate the change in
diameter by substituting
ε
transverse
for
ε
axial
, and diameter d for length L:
δ
transverse
=ε
transverse
d
.
!"
An aluminum rod has a cross-sectional area of 0.19635 in.
2
. An axial tensile load of 6000
lb. causes the rod to stretch along its length, and shrink across its diameter. What is the
diameter before and after loading? Report the answer in inches.
The rod has a circular cross section, so the cross-sectional area before the rod is
loaded is
A=
π
4
d
2
. Rewrite to solve for the initial diameter,
d=
√
4 A
π
=
√
4⋅0.19635 in.
2
π
=0.50000 in.
. When the rod is loaded, the axial strain is
ε
long
=
σ
E
=
P
AE
=
6000 lb.
0.19635 in.
2
in.
2
10×10
6
lb.
=0.00306
.
Poisson’s ratio
ν=
−ε
transverse
ε
long
, so
ε
transverse
=−ν⋅ε
long
=−0.33⋅0.00306=−0.00101
The change in diameter is
δ
transverse
=ε
transverse
⋅d =−0.00101×0.50000 in.=−0.000504 in.
The final diameter
d
f
=d
o
+δ
transverse
=0.50000in.−0.000504 in.=0.4995 in.
In a civil engineering structure, a dimensional change of half a thousandth of
an inch is insignificant, but in a machine it could affect performance.
Imagine a machine part that slides in a slot: if the part is loaded axially in
compression, Poisson’s effect could change a part that slides (slip fit) into a
part that sticks (press fit).
You can feel the effect of Poisson's ratio when you insert a rubber stopper or
a cork in a bottle. The Poisson's ratio of rubber is about 0.5, while cork is
about 0.0. If you try to push a rubber stopper into the neck of a bottle, the
material above the neck will shorten and thicken, making it difficult to insert
into the bottle. The harder you push, the more the stopper will expand in the
transverse direction, and this expansion is about 50% of the compression in
5 Named for Siméon Poisson, a French mathematician and physicist.
23
P
ε
axial
ε
transverse
corkrubber
P
P
shrinks
expands
P
P
A
Rod
becomes
longer
and
skinnier
under an
axial
load

Chapter 3: Poisson's Ratio and Thermal Expansion
the axial direction. Natural cork is made from the bark of the cork oak tree, and does not expand transversely when you
push on it. The only resistance comes from compressing the cork in the bottle neck, and friction.
Consider a block that is pulled in two directions by forces P
x
and P
y
. The strain in the
x direction due to the axial stress from P
x
is
ε
x axial
=
σ
x
E
. If P
x
is positive (tension),
then the strain is also positive...the bar is stretching along the x axis due to the action
of P
x
. However, tensile load P
y
is acting to shrink the bar in the x direction; the strain
due to this transverse load is
ε
x transverse
=−
ν σ
y
E
. Add these two strains to find the
total strain in the x direction,
ε
x
=
σ
x
E
−
νσ
y
E
=
1
E
(σ
x
−νσ
y
)
.
Similarly, the total strain in the y direction is
ε
y
=
σ
y
E
−
νσ
x
E
=
1
E
(σ
y
−νσ
x
)
.
Real blocks, of course, are three-dimensional. If the block is loaded in all three directions, calculate the strain in the x, y, and
z directions as
ε
x
=
1
E
(σ
x
−νσ
y
−νσ
z
)
,
ε
y
=
1
E
(σ
y
−νσ
x
−ν σ
z
)
, and
ε
z
=
1
E
(σ
z
−ν σ
x
−ν σ
y
)
.
!#
Calculate the strains in the x, y, and z directions for this steel block.
First, calculate the normal stress in the x, y, and z directions as the
force divided by the perpendicular surface that it acts on.
The stress in the x direction acts on the right face of the block, so the normal
stress is
σ
x
=
3kN
2cm×4 cm
∣
MPa m
2
10
3
kN
∣
(100cm)
2
m
2
=3.75 MPa
. The stress in the
y direction acts on the top of the block, so the normal stress is
σ
y
=
5kN
2cm×3 cm
∣
MPa m
2
10
3
kN
∣
(100cm)
2
m
2
=8.33 MPa
.
The stress in the z direction acts on the front face of the block, so the normal stress is
σ
z
=
−2 kN
3cm×4cm
∣
MPa m
2
10
3
kN
∣
(100cm)
2
m
2
=−1.67 MPa
. The load and stress are negative because they are compressive.
Next, calculate the strains. Since the block is steel, Young's modulus is 207 GPa and Poisson's ratio is 0.25.
ε
x
=
1
E
[σ
x
−νσ
y
−ν σ
z
]=
1
207×10
3
MPa
[3.75MPa −0.25(8.33 MPa)−0.25 (−1.67 MPa)]=1.01×10
−5
ε
y
=
1
E
[σ
y
−ν σ
x
−ν σ
z
]=
1
207×10
3
MPa
[8.33 MPa−0.25 (3.75 MPa )−0.25(−1.67 MPa)]=3.77×10
−5
ε
z
=
1
E
[σ
z
−ν σ
x
−ν σ
y
]=
1
207×10
3
MPa
[−1.67 MPa−0.25(3.75 MPa )−0.25(8.33 MPa )]=−2.26×10
−5
24
P
x
P
y
P
y
= 5 kN
P
x
= 3 kN
P
z
= 2 kN
4 cm
3 cm
2 cm
y
x
z

Chapter 3: Poisson's Ratio and Thermal Expansion
1
Heat a piece of steel, wood, or concrete, and it expands. Cool the same piece, and it
shrinks. Plot the strain as a function of temperature change, and for most materials, you
get a relatively straight line. The slope of the line is called the thermal expansion
coefficient, Greek letter α. It tells us how much strain we can expect for a given
temperature change. From the graph, the slope
α=ε/Δ T
. The units of α are strain
divided by temperature:
in./in.
°F
or
mm /mm
°C
, which we can write as °F
-1
or °C
-1
.
Substitute the definition of strain,
ε=δ/ L
, and we have
α=
δ
L(ΔT )
. Rewrite the
equation to solve for thermal deflection:
δ=α L(ΔT )
.
The thermal expansion coefficient is a materials property; different materials expand at different rates. For example,
aluminum expands about twice as much as steel for a given temperature change, because
α
Aluminum
=23×10
−6
°C
−1
and
α
Steel
=12×10
−6
°C
−1
. One reason we use steel as a reinforcement in concrete is
α
Concrete
=11×10
−6
°C
−1
, so the steel and
concrete expand and contract at roughly the same rate. If the matrix and reinforcement in a composite expand at different
rates, then the matrix and reinforcement may separate under repeated thermal cycles.
The change in temperature can be positive or negative, and is defined as the final temperature minus the original
temperature:
Δ T =T
f
−T
o
. If the material is cooled from 70°F to 40°F, the change in temperature is
Δ T =40 °F−70°F=−30 °F
. If the material is heated from 70°F to 90°F, the change in temperature is
Δ T =90 °F−70 °F=+20 °F
.
!$
A 5 m aluminum flagpole is installed at 20°C. Overnight, the temperature drops to -5°C. How much does the height
change, in millimeters? What is the final height of the flagpole, in meters?
First, calculate the change in length using
δ=α L(ΔT )
. From the Appendix, the thermal expansion coefficient
for aluminum is
α
Aluminum
=23×10
−6
°C
−1
. Next, calculate the final length by adding the change in length to the original
length.
Change in length
δ=α L (Δ T )=
23×10
−6
°C
5 m(−5 °C−20°C)
∣
10
3
mm
m
=−2.88 mm
. The negative sign indicates the
flagpole is getting shorter. Final length
L
f
=L+δ=5 m−
2.88 mm
∣
m
10
3
mm
=4.997 m
.
Two cantilever beams made of different materials have a measurable gap between their ends.
As the bars heat up, they grow towards each other and eventually meet if the temperature
rises enough. Each bar has a different thermal coefficient of expansion. How do we calculate
the temperature T
f
at which they meet? Consider that the gap between the two bars equals
δ
total
=δ
steel
+δ
brass
. Substitute the equation for thermal expansion, and we get
δ
total
=α
steel
L
steel
(Δ T
steel
)+α
brass
L
brass
(Δ T
brass
)
. The change in temperature is the same for
both materials, so
δ
total
=Δ T (α
steel
L
steel
+α
brass
L
brass
)
. Rewrite the equation to solve for
temperature change:
Δ T =
δ
total
α
steel
L
steel
+α
brass
L
brass
. The temperature change
Δ T =T
f
−T
o
,
so we can solve for the final temperature:
T
f
=T
o
+
δ
total
α
steel
L
steel
+α
brass
L
brass
.
25
steel
T
o
brass
L
steel
L
brass
T
f
δ
thermal (steel)
+ δ
thermal (brass)
Δ Temperature
Strain
ε
α

Chapter 3: Poisson's Ratio and Thermal Expansion
If the material is restrained from expanding or contracting while the temperature changes,
then stress builds within the part. Consider a bar of steel embedded in two blocks of
concrete. If the bar heats up, it will want to expand by an amount
δ=α L(ΔT )
. However,
the blocks of concrete prevent the bar from expanding, by exerting a force P on the bar. We
know from Chapter 2 that an axial load will cause a bar to deform an amount
δ=
PL
AE
.
However, the load P in this problem is compressive, so
δ=
−PL
AE
. Set the two deflections
equal to each other, and
α L(ΔT )=
−PL
AE
. Length L cancels from both sides, so
α( Δ T )=
−P
AE
. The thermal stress in the bar is
σ
thermal
=
P
A
, so we have
α(ΔT )=
−σ
thermal
E
. Solve for thermal stress:
σ
thermal
=−α E (Δ T )
. The thermal stress does not depend on the length of the
bar; it depends only on materials constants α and E and the temperature change.
!%
Two immovable concrete blocks are connected by a steel wire. At 72°F there is no stress in the wire.
If the wire cools from 72°F to 55°F, what is the stress in the wire?
Find these steel properties in the Appendix:
α=6.5×10
−6
°F
−1
and
E=30×10
6
psi
.
Thermal stress
σ=−α E (Δ T )=
−6.5×10
−6
°F
30×10
6
lb.
in.
2
(55 °F−72°F)
=3,315 psi
The positive sign indicates the wire is under a tensile stress. The wire cooled and wanted to shrink, but the concrete blocks
prevented it from shrinking, leaving the wire in tension.
!&
Two immovable concrete blocks are connected with a 2 inch by 2 inch square bar. At 72°F
there is no stress in the bar. If the bar heats from 72°F to 102°F, what is the stress in the bar?
How much force do the blocks exert on the bar?
Find these steel properties in the Appendix:
α=6.5×10
−6
°F
−1
and
E=30×10
6
psi
.
Thermal stress
σ=−α E (Δ T )=
−6.5×10
−6
°F
30×10
6
lb.
in.
2
(102°F−72 °F)
=−5,850 psi
The negative sign indicates the bar is under a compressive stress. The bar heated up and wanted to expand, but the
concrete blocks prevented it from expanding, leaving the bar in compression.
We can find the force exerted by the walls from the thermal stress:
σ
thermal
=
P
thermal
A
.Rewrite the equation to solve for
force:
P
thermal
=σ
thermal
A=
−5,850 lb.
in.
2
2in.×2 in.
=−23,400lb.
The negative sign shows that the force is compressive.
26
P
T
o
P
T
f
T
f
δ

Chapter 3: Poisson's Ratio and Thermal Expansion
Some thermal expansion problems require both the deflection and the stress equations. For
example, if this cantilever beam heats up sufficiently, it will meet the right-hand wall. If the
temperature continues to rise, stress will build up in the beam. If you know the initial length,
material, and temperatures T
o
and T
2
(but not temperature T
1
), how do you find the thermal
stress? Use the thermal deflection equation and the temperature change
Δ T =T
1
−T
o
to figure
out temperature T
1
, then use the thermal stress equation and the temperature change
Δ T =T
2
−T
1
to figure out σ
thermal
at temperature T
2
.
+,
Poisson's ratio is the decrease in transverse strain to the increase in longitudinal strain:
ν=
−ε
transverse
ε
long
Calculate the strains in an elastic block loaded in the x, y, and z directions as
ε
x
=
1
E
(σ
x
−νσ
y
−νσ
z
)
,
ε
y
=
1
E
(σ
y
−νσ
x
−ν σ
z
)
, and
ε
z
=
1
E
(σ
z
−ν σ
x
−ν σ
y
)
. If a load does not exist in one of the directions, then the stress term
for that direction is zero, and the equations become simpler.
Change in length due to a change in temperature is a function of the thermal expansion coefficient, the initial length, and the
change in temperature:
δ=α L(ΔT )
Stress due to a change in temperature is a function of the thermal expansion coefficient, Young's modulus, and the change in
temperature:
σ
thermal
=−α E (Δ T )
27
T
o
T
1
>T
o
no contact, σ = 0
contact, σ = 0
contact, σ > 0
T
2
>T
1
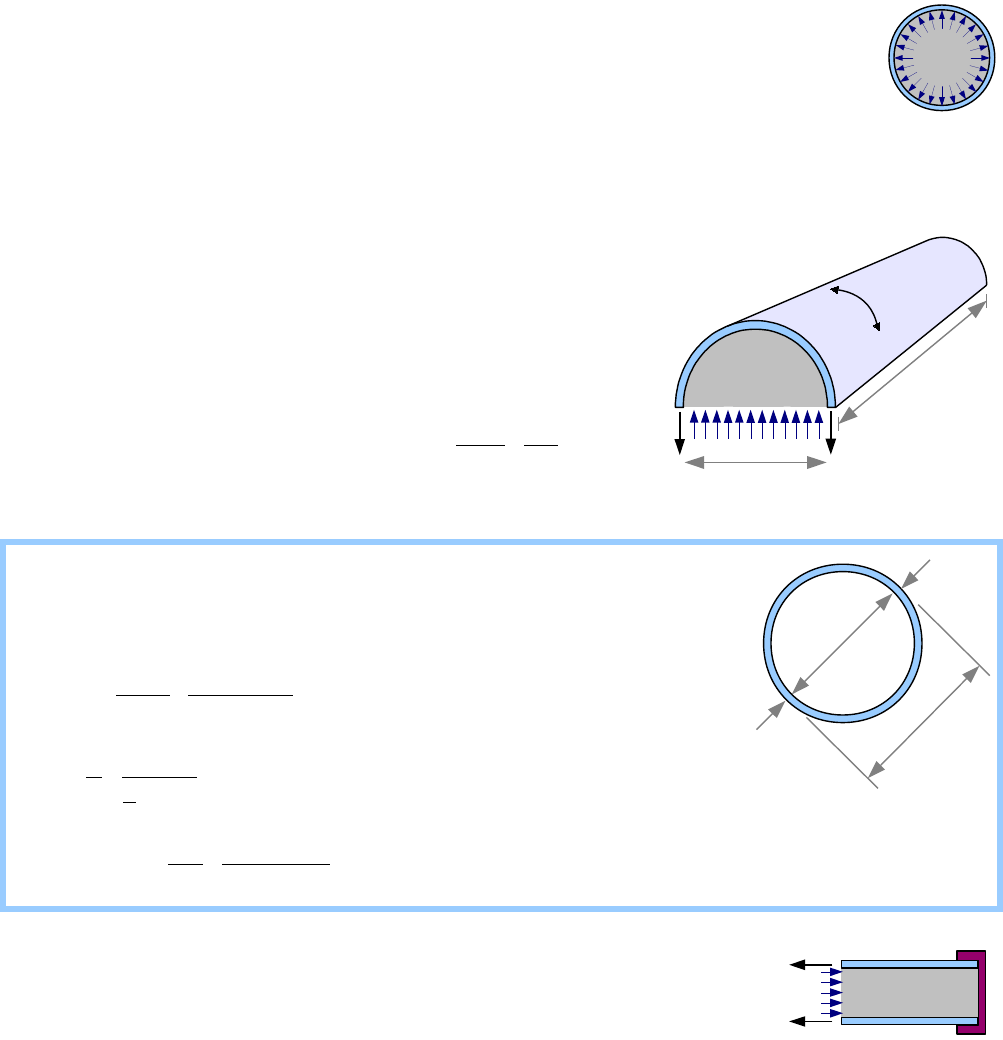
Chapter 4: Pressure Vessels and Stress Concentrations
2&3
,(3
A pressure vessel is a container holding a fluid (liquid or gas) under pressure. Examples include carbonated beverage
bottles, propane tanks, and water mains. Drain pipes are not pressure vessels because they are open to the atmosphere.
In a small pressure vessel such as a horizontal pipe, we can ignore the effects of gravity on the fluid. In the
17
th
century, French mathematician and physicist Blaise Pascal discovered that internal fluid pressure
pushes equally against the walls of the pipe in all directions, provided the fluid is not moving. The SI
pressure and stress unit, the pascal (Pa), is named after Pascal because of his work with fluid pressure. The
symbol for pressure is lower-case p, not to be confused with upper-case P used for point loads.
If the thickness of the wall is less than 10% of the internal radius of the pipe or tank, then the pressure vessel is described as
a thin-walled pressure vessel. Because the wall is thin, the stress in the wall is nearly the same on the inside and outside
surfaces of the wall. (Thick-walled pressure vessels have a higher stress on the inner surface than on the outer surface, so
cracks form from the inside out.)
Imagine cutting a thin-walled pipe lengthwise through the pressurized fluid
and the pipe wall: the force exerted by the fluid must equal the force exerted by
the pipe walls (sum of the forces equals zero). The force exerted by the fluid is
p⋅A= p d
i
L
where d
i
is the inside diameter of the pipe, and L is the length of
the pipe. The stress in the walls of the pipe is equal to the fluid force divided
by the cross-sectional area of the pipe wall. This cross-section of one wall is
the thickness of the pipe, t, times its length. Since there are two walls, the total
cross-sectional area of the wall is
2t L
. The stress is around the
circumference, also called the hoop direction, so
σ
hoop
=
p d
i
L
2t L
=
p d
i
2 t
. Hoop
stress is independent of the length of the pipe.
!"
A pipe with a 15 in. outside diameter and a 14 in. inside diameter carries pressurized
water at 110 psi. What is the hoop stress?
First, calculate the wall thickness, t. From the diagram, see that
d
o
=d
i
+2t
,
therefore
t =
d
o
−d
i
2
=
15 in.=14 in.
2
=0.5 in.
Next, check if the pipe is thin-walled. The ratio of the pipe wall thickness to the internal
radius is
t
r
i
=
0.5 in.
1
2
(14 in.)
=0.071<0.10
, so the pipe is thin-walled.
Hoop stress
σ
hoop
=
p d
i
2 t
=
110 psi⋅14in.
2⋅0.5in.
=1,540 psi
What if the pipe is capped? If the cap were loose, pressure would push the cap off the end. If the
cap is firmly attached to the pipe, then a stress develops along the length of the pipe to resist
pressure on the cap. Imagine cutting the pipe and pressurized fluid transversely. The force
exerted by the fluid equals the force along the length of the pipe walls.
28
p
L
d
i
Hoop
direction
p
p
d
i
d
o
t
t

Chapter 4: Pressure Vessels and Stress Concentrations
Pressure acts on a circular area of fluid, so the force exerted by the fluid is
P
fluid
=p⋅A= p
π
4
d
i
2
. The cross-sectional area of
the pipe wall
A=
π
4
d
o
2
−
π
4
d
i
2
=
π
4
(d
o
2
−d
i
2
)
. We can estimate the cross-sectional area of a thin-walled pipe pretty closely by
multiplying the wall thickness by the circumference, so
A≈π d
i
t
. The stress along the length of the pipe is
σ
long
=
P
fluid
A
pipe
=
pπ d
i
2
4π d
i
t
. Simplify by canceling π and one of the diameters:
σ
long
=
pd
i
4t
.
In a thin-walled pipe, hoop stress is twice as large as longitudinal stress. If the pressure in a pipe exceeds the strength of the
material, then the pipe will split along its length (perpendicular to the hoop direction).
Does the shape of the cap affect the longitudinal stress in the
pipe? No, because only the cross-sectional area of the pipe
matters. Typically, pressure vessels have concave or convex
domes, because flat caps tend to deflect under pressure, but
the shape has no effect on longitudinal stress in the pipe
walls.
A welded steel outdoor propane tank typically consists of a tube with two
convex hemispherical caps (right). Hoop stress controls the design in the
tube portion. Where the caps are welded to the tubes, longitudinal stress
controls the design. If the steel is all the same thickness (and the welds
are perfect), then the tank will fail in the tube section because hoop stress
is twice the longitudinal stress. A spherical tank (far right) only has
longitudinal stress, so it can handle twice the pressure of a tubular tank.
Think of a spherical tank as two hemispheres welded together; the weld
prevents the two halves from separating.
In conclusion, if you have a pipe or a tubular tank, use
σ
hoop
=
p d
i
2 t
. If you have a spherical tank, use
σ
long
=
p d
i
4t
.
The ASME Boiler Code recommends using an allowable stress
σ
allowable
=
1
4
σ
UTS
or
σ
allowable
=
2
3
σ
YS
, whichever is smaller.
!#
What is the minimum thickness of a spherical steel tank if the diameter is 10 feet, internal pressure is 600 psi, the tensile
strength of the steel is 65ksi, and the yield strength of the steel is 30 ksi?
First, calculate the allowable stress. Next, rewrite the stress equation for longitudinal stress (because this is a
sphere, not a pipe) to solve for wall thickness.
Based on tensile strength,
σ
allowable
=
1
4
σ
UTS
=
65 ksi
4
=16.25 ksi
. Based on yield strength,
σ
allowable
=
2
3
σ
YS
=
2⋅30 ksi
3
=20 ksi
; therefore, use 16.25 ksi because it is the smaller number.
Longitudinal stress
σ
long
=
p d
i
4 t
. Rewrite the equation for thickness,
t =
p d
i
4 σ
allowable
=
600 psi⋅10 ft
4⋅16.25 ksi
∣
ksi
10
3
psi
∣
12 in.
ft
=1.11in.
The welds in real steel tanks contain defects, which reduce the strength of the welds. We can measure the strength of welded
joints in the lab and compare them with the strength of the base metal. If the strengths match, we say the joint is 100%
efficient. The symbol for efficiency is the Greek letter eta,
η
.
29
p p
p
longitudinal stress
hoop stress
p

Chapter 4: Pressure Vessels and Stress Concentrations
!$
What is the minimum thickness of the spherical steel tank in Example #2 if the joint efficiency is 80%?
Use the same equations as before, except the allowable stress is multiplied by the joint efficiency.
Longitudinal stress
η
joint
σ
long
=
p d
i
4 t
, therefore
t =
p d
i
4 η
joint
σ
allowable
=
600 psi⋅10 ft
4⋅0.80⋅16.25 ksi
∣
ksi
10
3
psi
∣
12 in.
ft
=1.38in.
Pull a solid bar in tension, and the tensile stress in the bar is uniform within
the bar:
σ=
P
A
gross
where A
gross
is the gross cross-sectional area of the bar. If
the bar has a hole in it, we would expect the stress to be higher because
there is less material:
σ
net
=
P
A
net
where A
net
is the net cross-sectional area
of the bar (gross area minus the area of the hole). Experiments show the
stress is not uniform within the remaining solid material; instead, it is
highest next to the hole, and lower as you move away from the hole. We
say that the stress is concentrated next to the hole.
The maximum stress adjacent to the hole is
σ
max
=K σ
net
=K
P
A
net
, where
K is a stress concentration factor that depends on the size of the bar and the
diameter of the hole. In general, the smaller the radius, the higher the stress.
For example, cracks have very high stress concentrations at their tips,
exceeding the tensile strength of the material, even though the average
stress in the part is below the yield strength. This is why cracks grow.
One way to prevent a crack from growing
in a material is to drill a hole at its tip. The
drillhole has a larger radius, which reduces
the stress to below the yield strength of the
material, and the crack is blunted.
Stress concentrations can occur anywhere
there is a change in geometry with a small
radius, such as holes, fillets, and grooves.
In the 1930s, M.M. Frocht
6
published a
series of graphs relating K to the
dimensions of the bar and hole (or fillet or
groove), and R.E. Peterson published
scientific papers on fatigue cracks which
start at stress concentrations. Peterson's
book on stress concentration factors
7
is still
in print.
This graph is based on Frocht's original
work. Use a four-step process to solve
stress concentration problems:
6 M.M. Frocht, “Photoelastic Studies in Stress Concentration,” Mechanical Engineering, Aug. 1936, 485-489. M.M. Frocht, “Factors of
Stress Concentration Photoelastically Determined", ASME Journal of Applied Mechanics 2, 1935, A67-A68.
7 Walter D. Pilkey & Deborah F. Pilkey, Peterson's Stress Concentration Factors, 3
rd
ed., Wiley, 2008.
30
P
d
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
2.0
2.2
2.4
2.6
2.8
d / h
gross
K
h
gross
Circular hole in a rectangular cross-section bar loaded in tension
P
σ
P
σ
A
Net

Chapter 4: Pressure Vessels and Stress Concentrations
% Divide the hole diameter by the gross width of the bar to find the ratio
d /h
gross
.
- Find the value of K from the graph.
. Calculate the net cross-sectional area (gross cross-sectional area minus the cross-sectional area of the hole). The
easiest way to find this value is to multiply the net width by the thickness.
2 Calculate the maximum stress using
σ
max
=K
P
A
net
!%
A bar measuring 80 mm wide by 16 mm thick has a 20 mm diameter
hole in the center. The tensile load on the bar is 900 N. Calculate the
maximum stress in the bar due to the stress concentration. Report the
result in MPa.
Divide the hole diameter by the gross cross-sectional width
of the bar:
d
h
gross
=
20 mm
80 mm
=0.25
. Use the graph to find
K≈2.36
. The net cross-sectional area of the bar is the net width
times the thickness. The net width is the gross width minus the hole diameter:
A
net
=(80 mm−20 mm)16 mm=960 mm
2
Maximum stress is
σ
max
=K
P
A
net
=2.36
900 N
960mm
2
∣
MPa mm
2
N
=2.2 MPa
Use a similar four-step process to solve stress concentration problems in tensile bars having fillets or semicircular grooves.
% Divide the groove or fillet radius by the net width of the bar to find the ratio
r /h
net
.
- Find the value of K from the graph on the following page. Be sure to use the right curve!
. Calculate the net cross-sectional area at the groove or fillet.
2 Calculate the maximum stress using
σ
max
=K
P
A
net
!&
A 0.25 in. thick, 2 in. wide bar has two semicircular 3/8 in. radius
grooves. Find the maximum stress in the bar due to the stress
concentration. Report the result in ksi.
Net width
h
net
=2in.−2 (0.375in.)=1.25 in.
Calculate
r
h
net
=
0.375in.
1.25 in.
=0.30
. From the graph on the next page,
K ≈1.82
. The net cross-sectional area is the net width
times the thickness:
A
net
=1.25 in.×0.25 in.=0.3125 in.
2
. Max. stress is
σ
max
=K
P
A
net
=1.82
1 ton
0.3125 in
2
∣
2kips
ton
=11.6 ksi
31
P = 900 N
d = 20 mm
h
gross
= 80 mm
r = 3/8 in.
h
net
h
gross
= 2in.
P = 1 ton

Chapter 4: Pressure Vessels and Stress Concentrations
+,
Hoop stress in a pressure vessel is equal to the internal pressure times the inside diameter divided by twice the wall
thickness:
σ
hoop
=
p d
i
2 t
. This equation is used for pipes and cylinders.
Longitudinal stress in a pressure vessel is equal to the internal pressure times the inside diameter divided by four times the
wall thickness:
σ
long
=
p d
i
4t
. This equation is used for spherical pressure vessels.
For welded tanks, the ASME Boiler Code recommends using
σ
all
=
1
4
σ
UTS
or
σ
all
=
2
3
σ
YS
, whichever is smaller.
Stress at a stress concentration equal to the stress concentration factor times the average stress at the net cross-sectional
area:
σ
max
=K σ
net
. Use stress concentration graphs to find the value of K.
32
σ
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
1.2
1.4
1.6
1.8
2.0
r / h
net
K
Semicircular grooves and quarter-circle fillets in a rectangular
cross-section bar loaded in tension
0.8 0.9 1.0
2.2
2.4
2.6
2.8
P
r
h
net
Fillets
Grooves
Fillets
P
r
Grooves
h
net

Chapter 5: Bolted and Welded Joints
4&(5
"5"
Look at a steel bridge or steel skeleton of a building, and you see plates,
columns, and beams. They intersect at joints, which transmit load from
one member to the next. Large steel structures are typically bolted,
riveted, or welded together. The strength of the joint may determine the
strength of the structure.
Lap two steel plates, and pin them with a rivet or bolt. If you pull hard
enough, the plates will want to twist. You can prevent twisting by butting
the two main plates, and joining them with lapped splice plates.
Bolted joints have several failure modes. We can calculate the allowable
load of the joint for each failure mode; the lowest value is the limiting
case, and determines the strength of the joint.
+ The bolt could shear off, preserving the integrity of the plates; this is the least expensive type of failure
because bolts are cheaper and easier to replace than plates.
+ The bolt could crush the plate where it bears against the plate.
6+ The plate could tear across its gross cross-sectional area (thickness times overall width), away from
the bolt holes.
$+ The plate could tear across its net cross-sectional area (thickness times actual material width) along a
line of bolt holes.
-
Imagine if we glue two plates together, so that they overlap with an
area Overlap. Pull on the plates with a tensile load P
S
, and the shear
stress in the glue is
τ=
P
S
A
overlap
. If we know the allowable shear
strength of the glue, τ
all
, we can calculate the tensile load that can be
applied to the joint as
P
S
=A
overlap
τ
all
. Now replace the glue with a
bolt. The cross-sectional area of the bolt, A
B
, carries the shear stress of
the joint, so we can write
P
S
=A
B
τ
all
, where
A
B
=
π
4
d
2
and d is the
bolt diameter. The bolt has a much smaller cross-sectional area than the
area of the glue, which is compensated by the bolt's much higher shear
strength.
If we have more than one bolt of equal diameter and strength, then we
can multiply the strength of the joint by the number of bolts, N, so that
P
S
=A
B
τ
all
N
.
A bolt can carry the load through more than one shear plane. Define n
as the number of shear planes, and
P
S
=n A
B
τ
all
N
.
Appendix B3 lists allowable shear stresses for three bolt materials and two loading cases: either with the threads of the bolt
in the shear plane, or with the smooth shank of the bolt in the shear plane. A bolt is stronger if the threads are excluded from
the shear plane because the threads act as stress concentration sites.
33
P
P
P
P
P
P
P
P
P
P
P
P
P
S
P
S
A
overlap
P
S
P
S
A
B
P
S
P
S
P
S
P
S
One shear plane
Two shear planes

Chapter 5: Bolted and Welded Joints
!"
Two A-36 steel plates are joined with two splice plates and
eight 3/4 in. diameter A325 bolts. The plates are 6 in. wide and
1.5 in. thick; the splice plates are the same width, and 0.8 in.
thick. Bolt threads are excluded from the shear plane. Calculate
the load that the joint can support in order to resist shear
failure. Report the result in kips.
From Appendix B3, A325 bolts with threads excluded
from the shear plane have a shear strength of 30 ksi. The problem is symmetrical,
so either the four bolts in the left plate will fail in shear first, or the four bolts in the
right plate will fail first. Therefore, we can erase half of the diagram, and focus on
four bolts, and N = 4.
The load is carried by two shear planes per bolt, so n = 2.
P
S
=n A
B
τ
all
N =
2 shear planes
bolt
⋅
π
4
(0.75 in.)
2
shear plane
⋅30
kips
in.
2
⋅4 bolts=106 kips
.-
If one or more of the plates is crushed by the bolt, then the
area that is crushed equals the bolt diameter, d, times the plate
thickness, t. Multiply this area by the bearing strength of the
plate, and we have the allowable bearing load for a joint with
one bolt:
P
P
=d t σ
P−all
.
The allowable bearing load for a joint with multiple bolts is
P
P
=d t σ
P−all
N
.
If the main plate is thicker than the sum of the thicknesses of two splice plates, then use the sum of the splice plate
thicknesses for t.
The allowable bearing stress is listed in Appendix B4; it is 1.5 times the ultimate tensile strength of the plate material.
!#
Calculate the load that the joint in Example #1 can support in order to resist bearing failure. Report the result in kips.
From the Allowable Plate Stress table, A-36 steel plates have an allowable bearing strength of 87 ksi. The two
splice plates have a combined thickness of 1.6 in., which is greater than the main plate thickness of 1.5 in. Using the
smaller of the two numbers, t = 1.5 in.
P
P
=d t σ
P −all
N =
0.75in.
bolt
⋅1.5in.⋅87
kips
in.
2
⋅4 bolts=392 kips
-
The gross cross-sectional area of the plate some distance away from the bolt holes is the width, b, times the thickness, t.
Check the gross cross-sectional areas of both the main plate and the splice plates, and use the smaller of the two. Multiply
this area by the gross tensile strength of the plate to find the allowable gross tensile load for the joint:
P
G
=b t σ
G−allowable
.
The allowable gross tensile strength is 60% of the yield strength of the plate material, listed in Appendix B4.
34
P
P
P
P
P
P
P
P
Zones where the plate is crushed by the bolt
P
S
P
S
P
S
P
S
6"
1.5"
0.8"
P
S
P
S
P
S
P
S

Chapter 5: Bolted and Welded Joints
!$
Calculate the load that the joint in Example #1 can support in order to resist gross tensile failure. Report the result in kips.
From Appendix B4, A-36 steel plates have an allowable gross tensile strength of 21.6 ksi.
P
G
=bt σ
G−all
=6.0 in. ⋅1.5 in.⋅21.6
kips
in.
2
=194 kips
/-
The net cross-sectional area of the plate at the bolt holes is the gross cross-sectional area, A
G
, minus the cross-sectional area
of the holes, A
H
. Each hole has a cross-sectional area perpendicular to the direction of the load equal to the hole diameter,
d
H
, times the plate thickness, t:
A
H
=d
H
t
. As a rule of thumb for structural applications, use a hole diameter 1/8 inch or 3
mm larger than the nominal bolt diameter.
The plate will fail along the line of one set of holes. Defining the number of holes in the fracture plane as N
F
, the net cross-
sectional area is
A
N
=A
G
−A
H
=b t−N
F
d
H
t
. The allowable net tensile load is this area times the allowable net tensile
strength:
P
N
=(bt −N
F
d
H
t)σ
N−all
. The allowable net tensile strength, listed in Appendix B4, is half of the ultimate tensile
strength of the plate material.
Both joints have six bolts per symmetrical half, but the joint on the left has three holes in the fracture plane, while the joint
on the right has two holes in the fracture plane.
!%
Calculate the load that the joint in Example #1 can support in order to resist net tensile failure. Report the result in kips.
From Appendix B4, A-36 steel plates have an allowable net tensile strength of 29 ksi. The hole diameter is 1/8 in.
larger than the nominal bolt diameter, so
d
H
=3/4in+1/8in.=7/8 in.
P
N
=(bt −N
F
d
H
t )σ
N−all
=
(
6 in.⋅1.5 in.−2 holes
7/8 in. ⋅1.5in.
hole
)
29
kips
in.
2
=185 kips
35
P
N
P
N
P
N
P
N
Fracture
P
N
P
N
P
N
P
N
Fracture
N
F
= 2
N
F
= 3
P
G
P
G
P
G
P
G
Fracture
b
t/2
P
G
P
G
P
G
P
G
Fracture
b
t

Chapter 5: Bolted and Welded Joints
01
Punching holes in steel causes it to weaken, so a joint may be weaker than the base material. Analysis of the roof of the
Hartford Civic Center, which collapsed in January 1978 under a load of heavy wet snow, showed that some joint plates
consisted of 85% holes, 15% steel! This flaw was one of several design and construction errors that led to the roof collapse.
We can calculate the efficiency of the joint by dividing the minimum joint strength by the gross strength of the plate some
distance away from the joint.
!&
Calculate the efficiency of the joint in the previous Examples. Report the result in percent.
The minimum joint strength is 106 kips (bolt shear failure). The gross tensile load of the plate is 194 kips. Joint
efficiency is
η
joint
=
106 kips
194 kips
=0.55=55 %
.
η
joint
<100 %
indicates an overloaded joint will fail before the structure does. This is the better failure mode for
repairability, because it is easier to replace a bolt than to replace an I-beam.
η
joint
≪100 %
indicates a poorly designed
joint, which could be improved with stronger bolts, more bolts, or a better hole pattern.
η
joint
>100 %
indicates an overdesigned joint – the structure will fail before the joint.
.0
Use all of the previous steps. Solve for P based on bolt shear failure, bearing failure, gross tensile failure, and net tensile
failure. The lowest value of P is the limiting case. Divide this result by P
G
to find the efficiency of the joint.
36

Chapter 5: Bolted and Welded Joints
!'
Two A-36 steel plates are joined with two splice plates and
twelve 25 mm diameter A325-X high strength bolts. The
main plates are 150 mm wide and 10 mm thick; the splice
plates are 125 mm wide and 7 mm thick. Calculate the load
that the joint can support; report the result in kN. Calculate
the joint efficiency; report the result in percent.
Solve for P based on shear, bearing, gross tensile,
and net tensile; the lowest value is the limiting case. Divide
this result by P
G
to find the efficiency of the joint.
The “X” in A325 -X means bolts with threads
excluded from the shear plane. From the Bolt Shear Strength
table, these bolts have a shear strength of 207 MPa.
The problem is symmetrical, so we can erase half of the
diagram, and N = 6. The load is carried by two shear planes
per bolt, so n = 2.
P
S
=n A
B
τ
allowable
N =
2 shear planes
bolt
π
4
(25 mm)
2
shear plane
207MPa ⋅6 bolts
∣
10
3
kN
MPa m
2
∣
m
2
(10
3
mm)
2
=1220 kN
From Appendix B4, the allowable bearing stress in the plates is 600 MPa. The two splice plates have a total
thickness of 14 mm, which is thicker than the 10 mm thick main plate, therefore t = 10 mm.
P
P
=d t σ
P −allowable
N=
25 mm
bolt
10 mm ⋅600 MPa 6 bolts
∣
10
3
kN
MPa m
2
∣
m
2
(10
3
mm)
2
=900 kN
6 From Appendix B4, the allowable gross tensile stress is 150 MPa. The splice and main plates have different
thicknesses and widths, so calculate P
G
both ways. Note the splice plate total thickness
t=7 mm+7 mm=14 mm
.
Splice plates:
P
G
=b t σ
G −allowable
=
125mm ⋅14 mm⋅150MPa
∣
10
3
kN
MPa m
2
∣
m
2
(10
3
mm)
2
=263 kN
Main plate:
P
G
=bt σ
G −allowable
=
150mm ⋅10 mm ⋅150 MPa
∣
10
3
kN
MPa m
2
∣
m
2
(10
3
mm)
2
=225kN
. Use this lower value for P
G
.
$ From Appendix B4, the allowable net tensile stress is 200 MPa. Calculate P
N
both ways.
Splice plates:
P
N
=(b t−N
F
d
H
t)σ
N− allowable
=
(
125 mm⋅14 mm−2 holes
28 mm⋅14 mm
hole
)
200MPa
∣
10
3
kN
MPa m
2
∣
m
2
(10
3
mm)
2
=193 kN
Main plate:
P
N
=(b t−N
F
d
H
t)σ
N−allowable
=
(
150 mm ⋅10 mm−2 holes
28 mm ⋅10 mm
hole
)
200MPa
∣
10
3
kN
MPa m
2
∣
m
2
(10
3
mm)
2
=188 kN
The lowest value is 188 kN, so the joint will fail first by fracturing across a line of bolt holes.
57
P
min
=188 kN
and
P
G−main plate
=225 kN
.
η
joint
=
188 kN
225 kN
=0.84=84 %
37
10 mm
P
P
P
P
P
P
P
P
150 mm
125 mm
7 mm
Chapter 5: Bolted and Welded Joints
("5
Bolted and riveted joints contain holes which may act as stress
concentration sites. If joined plates have to be watertight, such as the
plates in a tank or a ship, then welding is a better choice. Welding is
also a good choice for parts that will not be disassembled in the
future. If you have ever soldered copper pipes together, you have
melted the solder but not the pipes. In welding, the weld metal and
the base metal melt together. In electric arc welding, an electric arc is
struck between an electrode and the base metal. The arc melts the
metals, and the electrode is gradually consumed. Welding problems in
this chapter focus on continuous electric-arc fillet welds in lapped
steel joints.
In cross-section, a fillet weld looks roughly like a right triangle. The
size l of a fillet weld is the length of a leg of the triangle. Overloaded
fillet welds fail by shearing along the throat h.
Using trigonometry,
h≈l sin 45°
. The weld supports shear load P
S
over area
h×L
, where L is the total length of the weld.
The allowable shear strength of the weld metal is
τ
allowable
=0.3 σ
UTS
, where
σ
UTS
is the ultimate tensile strength of the
weld metal (not the plate metal). Combining these equations, the load that the welded joint can support is
P
weld
=τ
allowable
×area=0.3σ
UTS
l sin 45° L=0.212⋅l⋅L⋅σ
UTS
Weld strength is proportional to weld size, weld length, and the strength of the electrode. Mild steel electrodes are classified
by their strength when welded, as Exx where xx is the ultimate tensile strength of the weld in ksi. For example, an E60
electrode has an ultimate tensile strength of 60 ksi, while an E70 electrode has a tensile strength of 70 ksi. Appendix B5
shows joint strengths for common plate thicknesses, using E60 and E70 electrodes. The values come from
P
weld
=0.212⋅l⋅L⋅σ
UTS
. Use Appendix B5 for common weld and plate sizes; use the equation for a different electrode such
as E90, or for a nonstandard plate size.
The strengths in the table are given as load per unit length; multiply this value by the total length of the weld to find the
shear load capacity of the welded joint. For example, a 6 in. long, 7/16 in. weld, using an E60 electrode, has a strength of
5.57 kips/in. The weld can support a load of
P
weld
=
6 in. 5.57kips
in.
=33.4 kips
.
Weld strength is not the only consideration when you design a welded joint. AISC recommends the following practices:
0 The end of a fillet weld creates a stress concentration. Run the weld around the end of the top plate to minimize
this effect. The length of the end return should be at least twice the nominal weld size:, a 3/8 in. weld should wrap around
the end at least 0.75 in. End returns are included in the total weld length, L.
" Two plates in a lap joint should lap at least five times the thickness of the thinner plate, and no less
than 1 inch. For example, a 3/8 in. thick plate welded to a 1/2 in. thick plate should lap at least
3/8 in.×5=1.875 in.
; an 1/8
in. plate welded to a 1/4 in. plate should lap at least 1 in. because
1/8 in.×5=0.625 in.
, which is less than an inch.
"( This rule applies to welds that are parallel to the loading direction. Two plates in a lap joint should lap
at least the width b of the narrower plate, unless the weld wraps fully around the end of the plate (i.e., the end returns meet
at the centerline). For example, a 3/8 in. thick, 6 in. wide plate welded along its sides to a 1/2 in. thick, 8 in. wide plate
should lap at least 6 in.
(8 The leg of a fillet weld can be made as large as the thickness of the top plate, or smaller; AISC recommends
ranges of size according to Appendix B6. If the top plate is less than 1/4 in. thick, then the leg can be as large as the
thickness; for thicker plates, the leg should be no larger than 1/16 in. less than the plate thickness.
01
Calculate the efficiency of a welded joint the same way as for a bolted joint: divide the joint load by the gross tensile load in
the plate with the smaller cross-section.
38
P
weld
end return
A A
Section A-A
detail
leg size, l
throat, h
P
weld
b
t
lap

Chapter 5: Bolted and Welded Joints
!(
Two 3/8 in. thick, 6 in. wide plates made of A36 steel are welded as
shown. Select the maximum size weld, and using an E70 electrode,
determine the joint strength, reporting the result in kips. Also,
calculate the efficiency of the joint.
From Appendix B6, the maximum weld size is 5/16 in. From
Appendix B5, a 5/16 in. weld made with an E70 electrode can
support a load of 4.63 kips/in. Each weld can support a load of
P
weld
=
4.63 kips
in.
6 in.
=27.78 kips
. Since there are two welds, the
joint strength is
P
S
=2×27.78 kips=55.56 kips
From Appendix B4, A36 steel has an allowable gross tensile strength of 21.6 ksi. The gross plate strength is
P
G
=b t σ
G−allowable
=6 in.⋅3/8in.⋅21.6 ksi=48.6 kips
.
η
joint
=
55.56 kips
48.60 kips
=1.14=114%
, which means that the joint is
stronger than the base metal. If the structure fails, the plate will crack while the joint remains intact.
!)
A 3/8 in. thick, 6 in. wide plate made of A36 steel is welded to a
1/2 in. thick, 8 in. wide plate using a 3/16 in. weld with an E80
electrode. Determine the joint strength, reporting the result in kips.
Also, calculate the efficiency of the joint.
Appendix B5 does not include data for the E80 electrode;
instead, use the weld strength equation. The length of each weld is
7 in. plus the 1 in. end return, or 8 in. The total weld length
L=2(8 in.)=16 in.
The tensile strength of an E80 weld is 80 ksi.
The joint can support a load of
P
weld
=0.212⋅l⋅L⋅σ
UTS
=0.212 ⋅
3
16
in.⋅16 in.⋅80
kips
in.
2
=50.9 kips
.
From Appendix B4, A36 steel has an allowable gross tensile
strength of 21.6 ksi. Use the smaller plate cross-sectional area (the
top plate). The gross plate strength is
P
G
=bt σ
G−allowable
=6 in.⋅
7
16
in.⋅21.6
kips
in.
2
=56.7 kips
.
η
joint
=
50.9 kips
56.7 kips
=0.90=90 %
, which means that the joint is 10%
weaker than the 6 in. plate. The joint could be strengthened in
several ways: a larger weld bead, a stronger weld electrode, a
continuous bead around the end of the top plate, or a weld bead
underneath.
39
P
weld
P
weld
3/8 in.
P
weld
P
weld
6 in.
3/8 in.
P
weld
P
weld
6 in.
7 in.
1 in.
3/8 in.
P
weld
P
weld
1/2 in.
P
weld
P
weld
P
weld
P
weld
Chapter 5: Bolted and Welded Joints
+,
Check bolted joints for shear, bearing, gross tensile, and net tensile failure; the lowest result is the limiting case. With a
symmetrical spliced joint, erase half of the joint and solve.
The allowable shear load for a bolted joint is
P
S
=n A
B
τ
allowable
N
where n is the number of shear planes per bolt, A
B
is the
cross-sectional area of the bolt (calculated from its nominal diameter), τ
allowable
is the allowable shear stress of the bolt (see
Appendix B3), and N is the number of bolts being considered.
The allowable bearing load for a bolted joint is
P
P
=d t σ
P−allowable
N
where d is the nominal bolt diameter, t is the plate
thickness (either the thickness of the main plate, or the combined thicknesses of the splice plates, whichever is smaller), and
σ
P-allowable
is the allowable bearing stress in the plate (see Appendix B4).
The allowable gross tensile load for a bolted joint is
P
G
=b t σ
G−allowable
where b is the plate width and σ
G-allowable
is the
allowable gross tensile stress in the plate.
The allowable net tensile load for a bolted joint is
P
N
=(b t−N
F
d
H
t) σ
N −allowable
where N
F
is the number of holes in the
fracture plane, d
H
is the nominal hole diameter (1/8 inch or 3 mm larger than d), and σ
N-allowable
is the allowable net tensile
stress in the plate.
The allowable tensile load of a fillet-welded joint is
P
S
=0.212⋅l⋅L⋅σ
UTS
. If standard plates are used with E60 or E70
electrodes, then use Appendix B5 to find the allowable tensile load.
The efficiency of a bolted or welded joint equals the lowest allowable load divided by the allowable load of the weaker of
the two plates some distance from the joint.
40

Chapter 6: Properties of Areas
9&*
Cross-sectional areas of beams, shafts, and columns have seven properties that we need in order to calculate stresses,
deflections, angles of twist, and buckling resistance in these structures. These properties are dimensions, area, centroid,
centroidal x-x and y-y axes, moment of inertia, radius of gyration, and polar moment of inertia.
*
The depth of a beam is the
distance from the top to the
bottom (the height of the beam).
The width is the distance from the
front to the back, as you face the
long length of the beam (the
thickness of the beam).
The area is the cross-sectional area. For a rectangular beam, the area is the width times the depth.
*1
Carefully balance a cardboard rectangle on a sharp
point. The location of the point on the rectangle is
called the centroid of the rectangle. The centroid of a
two-dimensional shape is analogous to the center of
gravity of a three-dimensional object.
Carefully balance the rectangle on a straightedge so
that two ends of the rectangle are parallel to the
straightedge. The location of the balance line is a
centroidal axis of the rectangle.
Every shape has a centroid and centroidal axes. We will use these properties in beam problems. Set a beam on edge, define
the x and y axes as horizontal and vertical, and we have x-x and y-y centroidal axes of the beam cross-sectional area.
'0
In everyday speech, the word “moment” means a short amount of time. In engineering
mechanics, moment is the product of a quantity and the distance from that quantity to a
given point or axis. For example, in Statics, a force acting on a wrench handle produces a
torque, or moment, about the axis of a bolt:
M =P× L
. This is the moment of a force.
We can also describe moments of areas. Consider a beam with a rectangular cross-section.
The horizontal centroidal axis of this beam is the x-x axis in the drawing.
Take a small area a within the cross-section at a distance y from the x-x
centroidal axis of the beam. The first moment of this area is
a× y
. The
second moment of this area is
I
x
=(a × y)× y=ay
2
. In Strength of
Materials, “second moment of area” is usually abbreviated “moment of
inertia”.
8
If we divide the total area into many little areas, then the moment
of inertia of the entire cross-section is the sum of the moments of inertia of
all of the little areas. We can also calculate the moment of inertia about the
vertical y-y centroidal axis:
I
y
=( a×x)×x=ax
2
. The x and y in I
x
and I
y
refer to the centroidal axis.
8 Engineers use the term “moment of inertia” out of habit. As A.P. Poorman states in Applied Mechanics in 1940, “the term moment of
inertia has been in use too long to be changed,” as it was first used in this sense by Swiss mathematician Leonhard Euler in the 18
th
century.
41
x x
depth
width
length
width
depth
P
L
x x
centroid
y
y
x x
y
a
y
y
x

Chapter 6: Properties of Areas
This rectangular beam cross-section has a depth of 16 cm and a width of 5 cm. We can
divide the beam into 8 equal segments 2 cm deep, 5 cm wide, so that each segment has an
area
a=2 cm×5 cm=10 cm
2
. The centroidal axis of segment #1 is 7 cm from the x-x axis
(y
1
=7 cm)
; the centroidal axis of segment #2 is 5 cm from the x-x axis
(y
2
=5 cm)
; and
so on. We can estimate the moment of inertia for the entire area as the sum of the moments
of inertia of the segments, written as
I
x
=
∑
1
n
a
i
y
i
2
where n = the total number of
segments, and i = the number of each segment (from 1 to n), or:
I
x
=a
1
y
1
2
+a
2
y
2
2
+a
3
y
3
2
+a
4
y
4
2
+a
5
y
5
2
+a
6
y
6
2
+a
7
y
7
2
+a
8
y
8
2
With numbers and units, we have:
I
x
=10 cm
2
(7 cm)
2
+10 cm
2
(5 cm)
2
+10 cm
2
(3 cm)
2
+10 cm
2
(1 cm)
2
+10 cm
2
(1 cm)
2
+10 cm
2
(3 cm)
2
+10 cm
2
(5 cm)
2
+10 cm
2
(7 cm)=1,680 cm
4
We can take the same beam and split it into 16 segments 1 cm deep.
I
x
=a
1
y
1
2
+a
2
y
2
2
+a
3
y
3
2
+a
4
y
4
2
+a
5
y
5
2
+a
6
y
6
2
+a
7
y
7
2
+a
8
y
8
2
+a
9
y
9
2
+a
10
y
10
2
+a
11
y
11
2
+a
12
y
12
2
+a
13
y
13
2
+a
14
y
14
2
+a
15
y
15
2
+a
16
y
16
2
We can estimate the moment of inertia as:
I
x
=5 cm
2
(7.5 cm)
2
+5cm
2
(6.5cm)
2
+5 cm
2
(5.5 cm)
2
+5 cm
2
(4.5cm)
2
+5 cm
2
(3.5 cm)
2
+5 cm
2
(2.5 cm)
2
+5 cm
2
(1.5 cm)
2
+5 cm
2
(0.5cm)
+5 cm
2
(0.5 cm)
2
+5 cm
2
(1.5cm)
2
+5 cm
2
(2.5 cm)
2
+5 cm
2
(3.5cm)
2
+5 cm
2
(4.5cm)
2
+5 cm
2
(5.5 cm)
2
+5 cm
2
(6.5 cm)
2
+5 cm
2
(7.5cm)=1,704.5 cm
4
As the segment size drops, the estimates converge on a solution. Split the beam into an infinite
number of infinitely-small segments to get the actual solution, derived from calculus:
I
x
=
bh
3
12
,
where b is the width and h is the depth. See Appendix C for moments of inertia of other simple
shapes.
!"
A rectangular beam has a depth of 16 cm and a width of 5 cm. What is the moment of inertia about the x-x centroidal axis?
Report the answer in cm
4
.
I
x
=
bh
3
12
=
5cm(16 cm)
3
12
=1,706.7cm
4
The estimated I
x
based on 8 segments was within 2% of the exact
answer; the estimated I
x
based on 16 segments is within 0.1%. Estimates can get us close to the exact solution, but in this
case, the math for the exact solution is less time-consuming (one equation instead of 16).
*1
Laminated structural wood beams are manufactured by glueing planks together. If we stand the planks vertically and glue
them along their facing surfaces, we can increase the moment of inertia. Since bending strength is directly proportional I, if
you double the moment of inertia you double the strength of the beam.
42
x x
1
5 cm
16
cm
2
3
4
5
6
7
8
y
1
x x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5 cm
16
cm
x x
h
b

Chapter 6: Properties of Areas
!#
Two
5cm×16 cm
rectangular planks are glued together as
shown. What is the moment of inertia about the x-x centroidal
axis? Report the answer in cm
4
.
The moment of inertia is
I
x
=
bh
3
12
=
10 cm(16cm)
3
12
=3,413.3cm
4
, which is twice the
moment of inertia of a single beam. Therefore, we can add the
moments of inertia of two cross-sections as long as they share the same centroidal axis:
I
xtotal
=I
x1
+I
x2
. A laminated
beam made of n parallel planks would have a moment of inertia of
I
xtotal
=
∑
1
n
I
x n
.
You can use this method even if the planks are not the same size, as long as they share the same centroidal axis.
!$
A
5cm×16 cm
rectangular plank is glued to an
8cm×3cm
as shown, so they share
the same neutral x-x axis. What is the moment of inertia about the centroidal axis?
Report the answer in cm
4
.
Add the moments of inertia of the individual planks:
I
x
=
b
1
h
1
3
12
+
b
2
h
2
3
12
=
b
1
h
1
3
+b
2
h
2
3
12
=
5cm(16 cm)
3
+3 cm(8 cm)
3
12
=1,834.7 cm
4
A compound beam shape may be made by welding or glueing
two beams together, or it may be made by extruding or rolling.
Aluminum extrusions are widely used in architecture, machine
parts, furniture, automotive components, and other consumer
goods. Steel is hot-rolled into railroad rails and wide-flange
structural steel beams, channels, and angles. Draw construction
lines on a cross-section and analyze it as if it were glued together
with rectangles sharing a common centroidal axis.
The moment of inertia for the entire shape is
I
xtotal
=I
x1
+I
x2
+I
x3
=
b
1
h
1
3
+b
2
h
2
3
+b
3
h
3
3
12
.
:#*1
If a beam is hollow and the hollow space
shares the same centroidal axis as the beam,
then we can subtract the moment of inertia of
the hollow area from the moment of inertia of
an equivalent solid beam. For a rectangular
beam with a rectangular hollow section,
I
xtotal
=I
x1
−I
x2
=
b
1
h
1
3
12
−
b
2
h
2
3
12
=
b
1
h
1
3
−b
2
h
2
3
12
43
5 cm
16 cm
x
x
3 cm
8 cm
5 cm
16 cm
x x
5 cm
=
10 cm
16 cm
x x
b
1
b
2
=
–
x xx xx x
h
1
h
2
1
x x
3
2
x x
=

Chapter 6: Properties of Areas
!%
A hollow rectangular beam has 1 cm thick walls, as shown. What is the moment of
inertia about the x-x centroidal axis? Report the answer in cm
4
.
Subtract the moment of inertia of the hollow space from the moment of inertia
of the outside dimensions.
I
x
=
b
o
h
o
3
12
−
b
i
h
i
3
12
=
9 cm(16cm)
3
−7 cm(14 cm)
3
12
=1,471cm
4
We can use the same technique for finding the moment of inertia of a hollow
tube. From calculus, the moment of inertia of a circle is
I
x
=
π d
4
64
, therefore the
moment of inertia of a hollow circle is
I
x
=
π d
o
4
64
−
π d
i
4
64
=
π (d
o
4
−d
i
4
)
64
.
!&
A standard 2" steel pipe has an outside diameter
d
o
=2.375 in.
and an inside diameter
d
i
=2.067 in.
What is the moment
of inertia about the x-x centroidal axis? Report the answer in in.
4
.
Subtract the moment of inertia of the hollow space from the moment of inertia of the outside dimensions.
I
x
=
π[(2.375 in.)
4
−(2.067 in.)
4
]
64
=0.6657 in.
4
+
The moments of inertia calculated in the previous examples were evaluated about the
centroidal axis of each shape. Sometimes we need to calculate the moment of inertia of a
beam about a different, noncentroidal axis. The Transfer Formula is
I =I
o
+ad
2
, where I
o
= moment of inertia about the x-x centroidal axis, I = moment of inertia about a parallel x'-
x' axis, a = the area of the shape, and d = the distance between the x-x centroidal axis and
the parallel x'-x' axis (the transfer distance). Note: the symbol d is also used for the
diameter of a circle; these quantities are different, even though they share the same symbol.
!'
A beam has a width of 5 inches and a depth of 6 inches. What is the moment of inertia
about the base of the beam, marked as the x'-x' axis? Report the answer in in.
4
.
The moment of inertia about the centroidal axis is
I
o
=
bh
3
12
=
5in.(6 in.)
3
12
=90 in.
4
and the cross-sectional area is
a=5in.×6 in.=30 in.
2
.
The distance from the x-x centroidal axis to the x'-x' axis
d=3 in.
Using the Transfer Formula,
I
x '
=I
o
+ad
2
=90in.
4
+(30in.
2
)(3 in.)
2
=360 in.
4
44
x x
d
a
x' x'
x x
d
5 in.
x' x'
6 in.
x x
16
cm
9 cm
7 cm
14
cm
–
d
o
d
i
=

Chapter 6: Properties of Areas
( ;$*1
Some compound cross-sections are made of segments
which do not share the same centroidal axis. As long as the
neutral axes are parallel, we can use the Transfer Formula
to find the moment of inertia of the compound beam. For
example, this beam cross-section consists of two
rectangular segments, and the x-x centroidal axis of the
beam is different from the x
1
-x
1
and x
2
-x
2
neutral axes of
segments #1 and #2. Using the Transfer Formula, we can
calculate the moment of inertia of each segment about the
x-x centroidal axis of the compound shape, then add the
results to obtain the total moment of inertia.
Using a 10-step process, we can calculate the moment of
inertia of the compound beam. This approach is sometimes
called a tabular method because you enter all of the
required numbers in a table as you solve the problem.
% Divide the compound beam into simple shapes, and
label the segments. This compound beam can be divided into
two segments; the method also works for complex shapes
made up of many simple shapes.
- Calculate the area a of each segment. Enter the areas
and their sum into a table. Be sure to list the units, because in
some problems, you may need to include a conversion factor
in the calculation.
a
1
=8 in.×3 in.=24 in.
2
a
2
=4 in.×12 in.=48in.
2
Seg- a
ment (in.
2
)
#1 24
#2 48
Sum 72
. Pick a Reference Axis, and label it on the diagram. In
theory, you can select any axis, but in practice, the math is
usually easier if you pick an axis along the top or bottom of
the complex shape, or along the centroidal axis of one of the
segments.
45
x x
x
2
x
2
x x
x
1
x
1
12 in.
3 in.
8 in.
4 in.
=
#1
#2
Ref. axis
#1
#2
#1
#2

Chapter 6: Properties of Areas
2 Draw the distance from the Reference Axis to the
centroidal axes of the segments, x
1
-x
1
and x
2
-x
2
. Label these
distances y
1
, y
2
, etc. Enter these values into the table.
Seg- a y
ment (in.
2
) (in.)
#1 24 13.5
#2 48 6
Sum 72
4 Calculate the product
a× y
for each segment, and
enter these values and their sum in the table.
Seg- a y ay
ment (in.
2
) (in.) (in.
3
)
#1 24 13.5 324
#2 48 6 288
Sum 72 612
9 Draw the distance from the Reference Axis to the x-x
centroidal axis of the complex shape. Calculate this distance
as
y=
∑
ay
∑
a
=
612 in.
3
72 in.
2
=8.5in.
46
x x
x
2
x
2
x
1
x
1
Ref. axis
#1
#2
y
y
2
y
1
x
2
x
2
x
1
x
1
Ref. axis
#1
#2
y
2
y
1

Chapter 6: Properties of Areas
< Draw the Transfer Distance d for each segment. This is
the distance from the centroidal axis of the segment to the
centroidal axis of the complex shape. Given the way this
beam is drawn,
d
1
= y
1
− y
and
d
2
=y− y
2
. For other
compound beams, you will have to figure out the formulas for
d
1
, d
2
, d
3
, etc. based on the drawing. Enter the results into the
table.
Seg- a y ay d
ment (in.
2
) (in.) (in.
3
) (in.)
#1 24 13.5 324 5
#2 48 6 288 2.5
Sum 72 612
= Calculate the product
a×d
2
for each segment, and
enter the results and their sum in the table. Be sure to
calculate
a×d
2
, not
a×d
...it’s an easy error to make.
Segment 1:
a×d
2
=24 in.
2
(5 in.)
2
=600 in.
4
Segment 2:
a×d
2
=48 in.
2
(2.5in.)
2
=300 in.
4
Enter these values and their sum into the table.
Seg- a y ay d ad
2
ment (in.
2
) (in.) (in.
3
) (in.) (in.
4
)
#1 24 13.5 324 5 600
#2 48 6 288 2.5 300
Sum 72 612 900
> Calculate I for each segment about its centroidal axis:
I
o1
=
bh
3
12
=
8in. (3 in.)
3
12
=18in.
4
I
o2
=
bh
3
12
=
4 in.(12 in.)
3
12
=576 in.
4
Enter these values and their sum into the table.
Seg- a y ay d ad
2
I
o
ment (in.
2
) (in.) (in.
3
) (in.) (in.
4
) (in.
4
)
#1 24 13.5 324 5 600 18
#2 48 6 288 2.5 300 576
Sum 72 612 900 594
%? Use the Transfer Formula to calculate I for the
compound shape.
I =
∑
I
o
+
∑
ad
2
=594 in.
4
+900 in.
4
=1494 in.
4
47
x x
x
2
x
2
d
1
x
1
x
1
Ref. axis
#1
#2
d
2
y
y
2
y
1

Chapter 6: Properties of Areas
:#( ;$*1
If the beam is hollow and the cavity does not share the same
neutral axis as the outline of the solid shape, then we need the
Transfer Formula. Let Segment #1 be the solid shape (with no
hole), and Segment #2 be the hole. In all calculations, the area
of the hole and the moment of inertia of the hole are negative
numbers. Thus a
1
, a
1
y
1
, a
1
d
1
2
, and I
1
are positive numbers; a
2
,
a
2
y
2
, a
2
d
1
2
, and I
2
are negative numbers.
% Divide the compound beam into simple shapes, and
label the segments. Segment #1 is a solid rectangle measuring
8 cm wide by 6 cm deep; Segment #2 is a hole measuring 6
cm wide by 2 cm deep.
- Calculate the area a of each segment.
a
1
=8 cm×6 cm=48 cm
2
a
2
=−(6 cm×2 cm)=−12 cm
2
Seg- a
ment (cm
2
)
#1 48
#2 -12
Sum 36
. Pick a Reference Axis, and label it on the diagram.
48
#2
#1
6 cm
8 cm
3.5 cm
2 cm
6 cm
Ref. axis
#2
#1
Chapter 6: Properties of Areas
2 Draw the distance from the Reference Axis to the
centroidal axes of the segments, x
1
-x
1
and x
2
-x
2
. Label these
distances y
1
, y
2
, etc. Enter these values into the table.
Seg- a y
ment (cm
2
) (cm)
#1 48 3
#2 -12 4.5
Sum 36
4 Calculate the product
a× y
for each segment, and
enter these values and their sum in the table.
Seg- a y ay
ment (cm
2
) (cm) (cm
3
)
#1 48 3 144
#2 -12 4.5 -54
Sum 36 90
9 Draw the distance from the Reference Axis to the x-x
centroidal axis of the complex shape. Calculate this distance
as
y=
∑
ay
∑
a
=
90 cm
3
36cm
2
=2.5cm
49
x
1
x
1
Ref. axis
#2
#1
y
1
y
2
x
2
x
2
x
1
x
1
Ref. axis
#2
#1
y
y
1
y
2
x
2
x
2
x x

Chapter 6: Properties of Areas
< Draw the Transfer Distance d for each segment. This is
the distance from the centroidal axis of the segment to the
centroidal axis of the complex shape. Enter the results into the
table.
Placing a hole in the upper part of this beam shifts the
centroidal axis downward, to where more of the material lies.
Since
d
1
=0.5 cm
, the centroidal axis of this hollow beam is
0.5 cm below the centroidal axis of a solid 6 cm × 8 cm solid
beam.
Seg- a y ay d
ment (cm
2
) (cm) (cm
3
) (cm)
#1 48 3 144 0.5
#2 -12 4.5 -54 2
Sum 36 90
= Calculate the product
a×d
2
for each segment, and
enter the results and their sum in the table. Be sure to
calculate
a×d
2
, not
a×d
...it’s an easy error to make.
Segment 1:
a×d
2
=48 cm
2
(0.5 cm)
2
=12 cm
4
Segment 2:
a×d
2
=−12 cm
2
(2 cm)
2
=−48cm
4
Seg- a y ay d ad
2
ment (cm
2
) (cm) (cm
3
) (cm) (cm
4
)
#1 48 3 144 0.5 12
#2 -12 4.5 -54 2 -48
Sum 36 90 -36
> Calculate I for each segment about its centroidal axis.
Note that I is negative for the hole.
I
o1
=
bh
3
12
=
8cm (6 cm)
3
12
=144 cm
4
I
o2
=−
bh
3
12
=−
6cm(2cm)
3
12
=−4 cm
4
Enter these values and their sum into the table.
Seg- a y ay d ad
2
I
o
ment (cm
2
) (cm) (cm
3
) (cm) (cm
4
) (cm
4
)
#1 48 3 144 0.5 12 144
#2 -12 4.5 -54 2 -48 -4
Sum 36 90 -36 140
%? Use the Transfer Formula to calculate I for the
compound shape.
I =
∑
I
o
+
∑
ad
2
=140 cm
4
−36 cm
4
=104 cm
4
Some compound beams have more than two segments; the 10-step procedure is the same, with more rows in the table.
50
x
1
x
1
Ref. axis
#2
#1
d
2
y
y
1
y
2
x
2
x
2
x x
d
1

Chapter 6: Properties of Areas
',$*1
The solution method for I
y
is the same as for I
x
, turned 90°.
Instead of y terms in the table, we have x terms.
% Divide the compound beam into three rectangles.
- Calculate the area a of each segment.
a
1
=4in.×1 in.=4 in.
2
a
2
=6in.×1 in.=6 in.
2
a
3
=4in.×2 in.=8in.
2
Seg- a
ment (in.
2
)
#1 4
#2 6
#3 8
Sum 18
. Pick a Reference Axis (easiest along the left edge or
along the right edge).
51
y
1
y
2
#2
#1
#3
y
1
y
2
4 in.
2 in.
1 in.
3 in.
1 in.
y
1
y
2
#2
#1
#3
Ref. axis

Chapter 6: Properties of Areas
2 Draw the distance from the Reference Axis to the
centroidal axes of the segments, y
1
-y
1
, y
2
-y
2
., and y
3
-y
3
. Label
these distances x
1
, x
2
, etc. In this problem, the y
1
-y
1
and y
3
-y
3
centroidal axes are the same.
Seg- a x
ment (in.
2
) (in.)
#1 4 2
#2 6 4.5
#3 8 2
Sum 18
4 Calculate the product
a×x
for each segment, and
enter these values and their sum in the table.
Seg- a x ax
ment (in.
2
) (in.) (in.
3
)
#1 4 2 8
#2 6 4.5 27
#3 8 2 16
Sum 18 51
9 Draw the distance from the Reference Axis to the y-y
centroidal axis of the complex shape. Calculate this distance
as
x=
∑
ax
∑
a
=
51in.
3
18 in.
2
=2.833 in.
52
y
1&3
y
1
y
2
y
2
#2
#1
#3
x
1
x
3
Ref. axis
y
1&3
y
2
x
2
y
1&3
x
y
1
y
2
y
2
y
#2
#1
#3
x
1
x
3
Ref. axis
y
1&3
y
2
y
x
2

Chapter 6: Properties of Areas
< Draw the Transfer Distance d for each segment. This is
the distance from the centroidal axis of the segment to the
centroidal axis of the complex shape. For this drawing,
d
1
=x− x
1
=d
3
and
d
2
=x
2
−x
.
Seg- a x ax d
ment (in.
2
) (in.) (in.
3
) (in.)
#1 4 2 8 0.83
#2 6 4.5 27 1.67
#3 8 2 16 0.83
Sum 18 51
= Calculate the product
a×d
2
for each segment.
Seg- a x ax d ad
2
ment (in.
2
) (in.) (in.
3
) (in.) (in.
4
)
#1 4 2 8 0.83 2.78
#2 6 4.5 27 1.67 16.67
#3 8 2 16 0.83 5.56
Sum 18 51 25.00
> Calculate I for each segment about its centroidal axis:
Seg- a x ax d ad
2
I
o
ment (in.
2
) (in.) (in.
3
) (in.) (in.
4
) (in.
4
)
I
o1
=
hb
3
12
=
1in.(4 in.)
3
12
=5.333 in.
4
I
o2
=
hb
3
12
=
6 in.(1in.)
3
12
=0.5 in.
4
I
o3
=
hb
3
12
=
2 in.(4in.)
3
12
=10.667in.
4
#1 4 2 8 0.83 2.78 5.33
#2 6 4.5 27 1.67 16.67 0.5
#3 8 2 16 0.83 5.56 10.67
Sum 18 51 25.00 16.50
%? Use the Transfer Formula to calculate I
y
for the
compound shape.
I
y
=
∑
I
o
+
∑
ad
2
=25.0 in.
4
+16.5in.
4
=41.5in.
4
53
d
3
y
1&3
x
y
1
y
2
y
2
y
#2
#1
#3
d
1
x
1
x
3
d
2
Ref. axis
y
1&3
y
2
y
x
2
b
h
CG

Chapter 6: Properties of Areas
Some shapes look like they require the Transfer Formula,
but creative segment choices make the problem easy.
Consider a beam with two hollow sections. The moment
of inertia could be calculated using the 10-step Transfer
Formula method with segments #1 (large rectangle), #2
(upper cavity), and #3 (lower cavity), but it is easier to
break it into rectangles sharing the same centroidal axis.
Calculate the moment of inertia of segment A (large
rectangle), subtract the moment of inertia of segment B
(two cavities joined together) and add the moment of
inertia of segment C (material between the two cavities).
The moment of inertia of a wide-flange beam made of
welded rectangular plates is easy to solve: subtract the
moments of inertia of the spaces to the left and right of
the web from the moment of inertia of a large rectangle.
Hot-rolled steel wide-flange beams, channels, and angles
have rounded internal and external corners, which makes
hand calculation of I
x
and I
y
difficult. Instead of
calculating these values, you can look them up in tables
(see Appendix D).
06
Columns are tall, thin structures loaded in compression which fail at stresses below the expected yield strength of the
material. Column analysis uses the radius of gyration to calculate failure loads. The radius of gyration is defined as
r
G
=
√
I / A
; the greater the radius of gyration, the more resistant the column is to buckling failure.
'
The moment of inertia of a cross-sectional area is
I
x
=
∑
1
n
a
i
y
i
2
relative to the x-x centroidal axis and
I
y
=
∑
1
n
a
i
x
i
2
relative
to the y-y centroidal axis. In torsion problems, we need a moment of inertia relative to the centroid of the shape, so we use
the radius of each elemental area from the center of gravity, r, to define the polar moment of inertia
J =
∑
1
n
a
i
r
i
2
. The units
are the same as for moment of inertia: in.
4
or mm
4
. From calculus, the exact equation for a circle is
J =
π
32
d
4
; for a hollow
circle,
J =
π
32
(d
o
4
−d
i
4
)
.
+,
Moments of inertia of simple shapes about the x-x centroidal axis are in Appendix C.
Use the Transfer Formula to find the moment of inertia about a noncentroidal axis, or for calculating the moment of inertia
of a compound shape:
I =I
o
+ad
2
.
The polar moment of inertia for a solid circle is
J =
π
32
d
4
, and for a hollow circle is
J =
π
32
(d
o
4
−d
i
4
)
.
54
x
x
x
2
x
2
x
1
x
1
=
A
–
B
+
x x
= –
A
B C
web
flange
C

Chapter 7: Torsion in Round Shafts
<&0
0
Many machine parts are loaded in torsion, either to transmit power
(like a driveshaft or an axle shaft in a vehicle) or to support a
dynamic load (like a coil spring or a torsion bar). Power
transmission parts are typically circular solid shafts or circular
hollow shafts because these shapes are easy to manufacture and
balance, and because the outermost material carries most of the
stress. For a given maximum size, more material is available along the
entire surface of a circle than at the four corners of a square.
Apply a torque T to a round shaft,
and the shaft will twist through an
angle θ. Twisting means the material
is deforming, so we have strain in the
material. The greatest strain,
γ
max
, is
at the surface, while strain is zero at
the center of the shaft. The strain
varies linearly from the center to the
surface of the shaft.
We saw in Chapter 2 that materials like steel and aluminum follow Hooke's law: the ratio of normal stress to normal strain
is Young's modulus:
E=σ/ε
. Young's modulus is a materials property (see Appendix B). In shear, the ratio of shear stress
to shear strain is the shear modulus:
G= τ/γ
(also in Appendix B). Therefore, the stress in the shaft also varies linearly
from the center to the surface of the shaft. We also saw in Chapter 2 that this stress is a shearing stress, so
τ=0
at the
center, and
τ= τ
max
at the surface.
Consider a small area a at a distance r from the center of the circle. If we define c as the distance from the
centroid to the surface of the circle, then the shear stress at r is
τ=
(
r
c
)
τ
surface
. Since shear stress is
force divided by area, the shear force acting on area a is
P
shear(a )
=τ a=
r τ
surface
a
c
. The torque on area
a is the force times the distance from the centroid:
T
(a)
=P
shear
r=
r
2
τ
surface
a
c
=
τ
surface
c
a r
2
. The total
torque on the entire circular area about the centroid is the sum of the torques on all the small areas that
comprise the circle, so
T =
τ
surface
c
∑
a r
2
. We've seen the last part of this equation before: the polar moment of inertia of a
circle is
J =
∑
a r
2
, therefore
T =
τ
surface
J
c
. For design purposes, only the maximum stress matters, so we usually drop the
subscript from the shear stress, understanding that we mean the stress at the surface, so we write
T =
τ J
c
. In many
problems, we know the applied torque and dimensions, but need the stress. Solving for stress,
τ=
Tc
J
.
55
r
c
area a
θ T
γ
max
γ
max
τ
max
τ
max
γ = 0 τ = 0
Shear
stress, τ
Shear strain, γ
Shear
modulus,
G

Chapter 7: Torsion in Round Shafts
!"
The torque on a ¼ inch diameter circular shaft is 5 ft.∙lb. What is the shear stress? Report the answer in ksi.
The distance from the centroid to the surface is
c=
d
2
=
0.25in.
2
=0.125 in.
. The polar moment of inertia of a
circle is
J =
π d
4
32
. Shear stress
τ=
Tc
J
=
5ft.⋅lb. 0.125 in. 32
π(0.25 in.)
4
∣
12in.
1ft.
∣
kip
10
3
lb.
=19.6 ksi
Once we have the shear stress, we can compare it with the allowable shear stress for this material. If the calculated stress is
higher than the allowable stress, then we can either select a stronger material or use a larger diameter shaft.
The shear stress in a hollow shaft varies linearly from the inside surface to the outside surface. Calculate the shear stress on
the inside surface as
τ=
Tr
i
J
where r
i
is the inside radius.
!#
A torque of 800 N∙m is applied to a hollow shaft. The inside diameter is 100 mm; the
outside diameter is 120 mm. What is the shear stress on the inside and outside surfaces?
Report the answer in MPa.
The distance from the centroid to the inside surface is
r
i
=
d
i
2
=
100 mm
2
=50 mm
.
The distance from the centroid to the outside surface is
c=
d
o
2
=
120mm
2
=60 mm
.
The polar moment of inertia of a hollow circle is
J =
π(d
o
4
−d
i
4
)
32
. We use the same J for both the inside and the outside
shear stress calculations.
Shear stress on the inside surface:
τ
i
=
Tr
i
J
=
800 N⋅m 50 mm 32
π[(120 mm)
4
−(100 mm)
4
]
∣
MPa m
2
10
6
N
∣
(10
3
mm)
3
m
3
=3.80 MPa
.
Shear stress on the outside surface:
τ
o
=
Tc
J
=
800 N⋅m 60 mm 32
π[(120 mm)
4
−(100 mm)
4
]
∣
MPa m
2
10
6
N
∣
(10
3
mm)
3
m
3
=4.55 MPa
In some problems, we know the applied torque and the shear strength of the material, and we need to calculate the minimum
diameter that will work. Write the shear stress equation algebraically, substituting
π d
4
32
for J and
d
2
for c. Now rewrite
the equation to solve for diameter:
d=
3
√
algebraic expression
.
56
r
i
τ
max

Chapter 7: Torsion in Round Shafts
*#0
Normal strain is defined as the change in length of tensile
member divided by its original length:
ε=δ/ L
. We can
define shear strain on a torsion member as the change in
location of a point on the surface of the shaft divided by the
length of the shaft:
γ=δ
shear
/ L
.
The angle of twist, θ, is measured in radians, so we can
substitute
δ
shear
=c θ
. Now the shear strain is
γ=c θ/ L
.
Substitute this value in the equation for shear modulus, and
G=
τ
γ
=
τ L
c θ
. Rewrite the equation to find the angle of twist
θ=
τ L
G c
.
Since shear stress
τ=
Tc
J
, we can substitute this expression into the angle of twist equation to get
θ=
τ L
G c
=
Tc
J
L
Gc
=
TL
JG
.
!$
A solid round aluminum shaft has a maximum allowable shear stress of 80 MPa. The shaft is 10 cm in diameter and 1 m
long. What is the angle of twist? Report the answer in radians and in degrees.
From Appendix B, the shear modulus of aluminum is
G=28×10
3
MPa
. The angle of twist is
θ=
τ L
G c
=
80 MPa 1 m
28×10
3
MPa
1
2
(10cm)
∣
100cm
m
=0.057 rad
Convert to degrees using the conversion button on your calculator, or use the Factor-Label Method of Unit Conversion:
0.057rad
∣
180°
π rad
=3.3°
!%
A hollow round steel shaft has a torque of 600 ft.lb. The shaft has an outside diameter of 1.25 in., an inside diameter of
1.10 in., and a length of 36 in. What is the angle of twist? Report the answer in radians and in degrees.
From Appendix B, the shear modulus of steel is
G=12,000 ksi
. The angle of twist is
θ=
T L
JG
=
32 T L
π d
4
G
=
32 ⋅600 ft.lb.⋅36 in. in.
2
π[(1.25 in.)
4
−(1.10 in.)
4
]12,000 kip
∣
kip
10
3
lb.
12 in.
ft.
=0.225 rad
Convert to degrees using the conversion button on your calculator, or use the Factor-Label Method of Unit Conversion:
0.225 rad
∣
180°
π rad
=12.9°
Looking at the equations, you can see that the angle of twist is directly proportional to length: if you double the length of the
shaft, the angle of twist doubles. In a tensile member, if you double the length the elongation doubles. Shear stress is
independent on length, just as normal stress is independent of the length of a tensile member.
57
θ
c
δ
shear
L
T

Chapter 7: Torsion in Round Shafts
If a shaft has a uniform diameter along its length, then the maximum shear stress at the
surface is
τ=
Tc
J
. Many shafts in machines have different diameters in different
locations, such as at the flange of an axle shaft, or adjacent to a bearing surface. A
sudden change in diameter creates a stress concentration. The maximum stress in the
smaller diameter section, at the base of the fillet, is
τ= K
Tc
J
where K is the stress
concentration factor. Other dimensional changes, such as keyways and transverse
through-holes, also create stress concentrations in shafts.
Look at the diagram of the shaft: the
fillet radius meets the flat face of the
large diameter portion of the shaft. The
two shaft diameters and fillet radius are
all independent variables, so the stress
concentration graph has several curves,
each for a different ratio of shaft
diameters. Use a five-step process for
calculating the maximum shear stress at
the stress concentration site:
% Divide the fillet radius by the
smaller shaft diameter find the ratio r/d.
- Divide the larger shaft diameter
by the smaller shaft diameter find the
ratio D/d.
. Using these two values, find the
value of K from the graph. If your
calculated D/d does not match the
values on the graph, interpolate. For
example, if r/d = 0.06 and D/d = 1.15,
then K≈1.35.
2 Calculate c and J using the
smaller shaft diameter.
4 Calculate the maximum stress
using
τ= K
Tc
J
.
!&
A 2¼ inch diameter shaft is welded to a 3 inch diameter shaft. The weld bead is ground to a radius of 0.125 inches. If the
torque is 600 ft.lb., what is the maximum shear stress at the fillet? Report the answer in ksi.
Calculate the ratios
D
d
=
3in.
2.25in.
=1.33
and
r
d
=
0.125 in.
2.25in.
=0.056
. Use the 1.33 line on the graph to find the
stress concentration factor
K≈1.65
.
τ
max
=K
Tc
J
=K T
d
2
32
πd
4
=
16 K T
πd
3
=
16⋅1.65⋅600ft.⋅lb.
π(2.25 in.)
3
∣
12 in.
ft.
∣
kip
10
3
lb.
=5.31ksi
58
r
d
D
location of
maximum stress
T
σ
0.0 0.02 0.04 0.06 0.08 0.10 0.12
1.0
1.2
1.4
1.6
1.8
r / d
K
Fillet in a stepped shaft loaded in torsion
2.0
2.2
2.4
2.6
1.09
2.00
1.50
1.20
1.33
r
d
D
T
D/d

Chapter 7: Torsion in Round Shafts
+,
Shear stress on the surface of a round solid or hollow shaft is the torque times the distance from the center to the outside
surface, divided by the polar moment of inertia:
τ=
Tc
J
The angle of twist of a round solid or hollow shaft can be calculated with
θ=
τ L
G c
or with
θ=
TL
JG
, depending on the
available input variables. With a stepped shaft, the maximum stress is
τ= K
Tc
J
where K is the stress concentration factor.
59

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
=&0@ @'
"
The way a part is loaded determines whether it is called a tensile or compressive
member, a torsional shaft, or a beam. If you take a ½ inch diameter steel rod and pull
it lengthwise with a load P, the rod will develop a tensile stress
σ=P / A
where A is
the cross-sectional area of the rod. Loading the rod in tension parallel to its axis
makes the rod a tensile member; loading it in compression parallel to its axis makes it a
compressive member. If you twist the steel rod with torque T, then we call it a
torsional shaft.
If loading is perpendicular (transverse) to its axis so that the rod bends,
then the rod is called a beam. You can load a beam with point loads,
uniformly distributed loads, or nonuniformly distributed loads. A
swimmer standing on the end of a diving board is an example of a point
load: a force applied at a single point on the beam. This point load P
could be the weight of an object on the beam, or it could be a load applied
by a cable or rod attached to the beam at that point. Typically, the left end
of the beam is marked “A” and the right end is marked “B”. For each
loaded beam we draw beam reactions: reaction forces R
A
and R
B
for a
simply supported beam; reaction force R
B
and reaction moment M
B
for a
cantilever beam.
The symbols for supports indicate the reactions that develop at the
support. For example, support “A” is pinned, like a hinge, so the symbol for the
support is a triangle. A pinned support may have vertical and horizontal reaction
forces. The beam at the right has no applied horizontal loads, therefore R
Ax
= 0. In
the beam problems in this chapter, there are no applied horizontal forces, so the
horizontal reaction force is zero, and the vertical reaction forces R
Ay
and R
By
are
abbreviated R
A
and R
B
.
A roller support allows the beam to move freely horizontally; the symbol is a
circle. A roller support has only a vertical reaction force. A beam supported by a
pin at one end and a roller at the other end is called a simply-supported beam.
A cantilever beam is embedded in a wall, so the beam has reaction forces as well
as a reaction moment. The horizontal reaction force
R
Bx
=0
if there are no
horizontal applied forces, so the vertical reaction force R
By
is abbreviated R
B
.
The weight of a beam is a uniform distributed load. The weight per unit length,
w, typically has units of lb./ft., kips/ft., or kN/m. Consider a wide-flange beam,
or “W-beam,” having a cross-section that looks like a Courier font capital letter I.
The U.S. Customary W-beam designation system has two numbers: the first is
the nominal depth, and the second is the weight per unit length. For example, a
W24×162 beam has a nominal depth of 24 inches and a weight per unit length
w=162 lb./ft.
. If the beam is 10 feet long, then the total weight, W, of the beam is
W =wL=
162lb.
ft.
10 ft.
=1,620 lb.
In Canada, W-beams are specified in SI (metric) units. These beams are designated by mass, not weight: a W250×115 wide
flange beam has a nominal depth of 250 mm and a mass per unit length of 115 kg/m. From Newton’s Second Law,
force=mass×acceleration
, or in this case,
weight=mass×acceleration of gravity
. The SI unit of force and weight is the
newton (N), defined as
1 N=1
kg m
s
2
, and the acceleration of gravity is
9.81 m/s
2
. The weight per unit length of a
W250×115 wide-flange beam is
w=
115 kg
m
9.81m
s
2
∣
N s
2
kg m
∣
kN
10
3
N
=1.13kN/m
. If the beam is 4 m long, then the total
60
P
P
T
=
P
R
B
M
B
=
P
R
B
R
A
P
R
By
M
B
P
R
By
R
Ay
R
Ax
R
Bx
A B
A B
A B
A B
w
R
B
R
A
A B

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
weight of the beam is
W =wL=
1.13kN
m
4 m
=4.51 kN
.
You can also calculate the weight per unit length from the cross-sectional area and the specific weight of the material.
Specific weight is weight divided by volume:
γ=W /V
. The volume of a beam of uniform cross-section is the cross-
sectional area times the length:
V = A⋅L
. Combining,
γ=
W
V
=
W
A⋅L
or
γ⋅A=
W
L
. Weight per unit length
w=
W
L
=γ⋅A
.
!"
What is the weight per unit length of a 1 inch diameter steel rod? Report the answer in lb./ft.
The cross-sectional area of a circle
A=
π
4
d
2
. The specific weight of steel is 490 lb./ft.
3
.
Weight per unit length
w=ρ⋅A=
γ π d
2
4
=
490lb.
ft.
3
π(1 in.)
2
4
∣
ft.
2
(12 in.)
2
=2.67lb./ft.
A distributed load may run the length of the beam
(like the beam's weight), may run along a portion of
the beam, or may be nonuniform.
0,
You can calculate the reaction forces for a symmetrically-loaded, simply-supported beam by dividing the total load by 2,
because each end of the beam carries half the load. The reactions for the beam with a point load are
R
A
=R
B
=P /2
.
!#
Calculate the reaction forces R
A
and R
B
for a beam with a 30 kN load at the midspan.
Divide the total load by 2 to obtain the reaction forces,
R
A
=R
B
=
P
2
=
30 kN
2
=15 kN
A simply-supported beam with a uniform distributed load also has a symmetrical loading pattern. Divide the total load on
the beam by 2 to find the reaction forces.
!$
Calculate the reaction forces R
A
and R
B
for a 10-ft. beam with a 480 lb./ft. uniformly
distributed load. Report the answer in kips.
Multiply the uniform distributed load by the length to find the total load on
the beam:
W =wL
. Divide the total load by 2 to obtain the reaction forces,
R
A
=R
B
=
W
2
=
wL
2
=
480lb.
ft.
10 ft. 1
2
∣
kip
1000 lb.
=2.4 kips
61
30 kN
R
B
R
A
A B
4 m 4 m
480 lb./ft.
R
B
R
A
A B
10 ft.
w
R
B
R
A
A B
w
R
B
R
A
A B

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
For beams with nonsymmetrical loading, we need two equations from
Statics: the sum of the vertical forces equals zero, and the sum of the
moments about a point equals zero. The moment about a point is the
force acting on an object times the perpendicular distance from the
force to the pivot point. Whether the object is a blob or a beam, the
moment about point A is
M
A
=P⋅x
.
You can pick a pivot point at either end of a simply-supported beam. Most
students find it easier to select the left end of the beam, point A. Since moment has a
magnitude and a direction (clockwise or counterclockwise), we need to establish a
convention for positive and negative moments. We’ll select counterclockwise as positive,
symbolized as , and start adding up the moments about point A. The load acts at a
distance x from point A. Think of point A as a hinge point…the load causes the beam to
rotate clockwise about point A, so the moment is negative. The reaction force R
B
acts at a
distance L from point A, and causes the beam to rotate counterclockwise about point A, so the moment is positive. The
moment about point A is
∑
M
A
=0=−Px+R
B
L
. Now solve for the reaction force
R
B
=
Px
L
. Use the sum of the
forces in the vertical direction to calculate the other reaction force. Forces have magnitude and direction; pick upwards as
positive, so
∑
F
y
=0=R
A
−P+R
B
. Now solve for the reaction force
R
A
=P−R
B
.
!%
Calculate the reaction forces R
A
and R
B
for this simply-supported beam.
Redraw the diagram, marking the distances to all loads and reactions from point
A.
The moment about point A is
∑
M
A
=0=−40 kN⋅3 m+R
B
⋅10 m
.
Rewrite the equation to find the reaction force
R
B
=
40 kN⋅3 m
10 m
=12 kN
.
Use the sum of the forces in the vertical direction to calculate the other reaction force:
∑
F
y
=0=R
A
−40 kN+12 kN
.
Rewrite the equation to find the reaction force
R
A
=40 kN−12 kN=28 kN
.
You can check the answer by solving the sum of the moments about point B.
Most of the applied load is supported by the left end of the
beam. Intuitively, this makes sense because the load is closer
to the left end of the beam. Flip the beam upside down and it
looks like two children on a see-saw: the pivot point has to
be closer to the heavier child in order to balance the see-saw.
Use the same technique for a simply-supported beam with multiple point loads.
62
P
R
A
M
A
A B
x
P
x
A
M
A
P
R
B
R
A
A B
x
L
40kN
R
B
R
A
A B
3m
7m
40kN
A B
3m
10m
40kN
R
A
A B
R
B
12kN
40kN
A B
12kN
28kN
12kN
28kN

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
!&
Calculate the reaction forces R
A
and R
B
for a beam with two point loads.
Redraw the diagram, marking the distances to all loads and reactions from
point A. This step may seem to be a waste of time, but as the loading conditions
become more complicated, it becomes more important to redimension the drawing, in
order to keep track of the distances used in the Sum of the Moments calculation.
The moment about point A is
∑
M
A
=0=−5 lb.⋅3 in.−12 lb.⋅6 in.+R
B
⋅10 in.
Rewrite the equation to find the reaction force
R
B
=
5lb.⋅3 in.+12 lb.⋅6 in.
10 in.
=8.7 lb.
Sum of the forces
∑
F
y
=0=R
A
−5 lb.−12 lb.+8.7lb.
Rewrite the equation to find the reaction force
R
A
=5 lb.+12 lb.−8.7 lb.=8.3 lb.
If a uniformly distributed load is not symmetrical, then
we need to convert the distributed load into a point
load equivalent to the total load
W =wL
1
where L
1
is
the length of the distributed load. The equivalent point
load is located at the centroid of the distributed load…
the center of the rectangle. Use the equivalent load
diagram for calculating the reaction forces.
!'
Calculate the reaction forces R
A
and R
B
for a beam
with a uniform distributed load of 800 N/m. Report
the result in N.
Draw an equivalent load diagram, placing
the equivalent load at the centroid of the distributed
load. Use the equivalent load diagram to find the
reaction forces.
The distributed load runs for 2m, so the location of the equivalent load is 1m from the left end of the distributed load, or
1.8m from point A. The equivalent load
W =wL=
800 N⋅2 m
m
=1600 N
.
The moment about point A is
∑
M
A
=0=−1600 N⋅1.8 m+R
B
⋅6 m
.
Rewrite the equation to find the reaction force
R
B
=
1600 N⋅1.8 m
6 m
=480 N
.
Sum of the forces
∑
F
y
=0=R
A
−1600 N +480 N
. Solve for the reaction force
R
A
=1600 N−480 N =1120 N
.
63
5 lb.
R
B
R
A
A B
3"
A B
R
B
3" 4"
12 lb.
R
A
5 lb.
12 lb.
3"
6"
10"
w
R
B
R
A
A B
=
L
1
W
R
B
R
A
A B
L
2
Load diagram
Equivalent load diagram
800 N/m
R
B
R
A
A B
=
R
B
R
A
A B
Load diagram
Equivalent load diagram
0.8 m 2 m 3.2 m
1.8 m
6 m
1600 N

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
Use the same approach for a nonuniformly distributed
load. Again, the location of the equivalent load is at the
centroid of the distributed load. The centroid of a
triangle is one third of the distance from the wide end of
the triangle, so the location of the equivalent load is one
third of the distance from the right end of this beam, or
two thirds of the distance from the left end.
The load varies from 0 at the left end to w at the right
end; therefore, the total load is the average of these
loads times the beam length:
W =
(
0+w
2
)
L=
wL
2
. If the beam has point loads and distributed loads, draw an equivalent
load diagram with the applied point loads and the equivalent point loads, then solve like Example #5.
0A
A simply-supported beam is supported by a pinned connection at one end and a roller support at the other; all applied loads
lie between these two points. An overhanging beam extends beyond one or both supports. The solution method is the same
as for simply-supported beams: use the sum of the moments about one of the support points to find the reaction at the other
support point.
!(
Calculate the reaction forces R
A
and R
B
for an overhanging beam with two point
loads.
Redraw the diagram, marking the distances to all loads and reactions from
point A.
The moment about point A is
∑
M
A
=0=50 kN⋅5 m−30 kN⋅11m+ R
B
⋅15 m
.
Notice the 50 kN load produces a positive (counterclockwise) moment about point
A, while the 30 kN load produces a negative (clockwise) moment about point A.
Rewrite the equation to find the reaction force
R
B
=
−50 kN⋅5 m+30 kN⋅11m
15 m
=5.33 kN
Sum of the forces
∑
F
y
=0=R
A
−50 kN−30 kN+5.33 kN
. Solve for the
reaction force
R
A
=50 kN +30 kN−5.33 kN=74.67 kN
.
Solve for the reactions to a distributed load on an overhanging beam the same way as for a distributed load on a simply-
supported beam: draw an equivalent load diagram, then use the sum of the moments and the sum of the forces to find the
reactions.
64
R
B
R
A
A B
=
R
B
R
A
A B
Load diagram Equivalent load diagram
L
2L/3
w W
L
A B
R
B
R
A
50 kN 30 kN
5 m
11 m 4 m
A B
50 kN 30 kN
R
B
R
A
5 m
11 m
15 m

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
!)
Calculate the reaction forces R
A
and R
B
for an
overhanging beam with a uniform distributed
load.
Draw an equivalent load diagram,
marking the distances to all loads and reactions
from point A. We do not need the dimensions to
the ends of the overhangs, because there are no
loads outside of the two supports.
The distributed load runs for 9 ft., so the location of the equivalent load is 4.5 ft. from the left end of the distributed load,
or 1.5 ft. to the right of point A. The equivalent load
W =wL=
60lb.⋅9 ft.
ft.
=540 lb.
The moment about point A is
∑
M
A
=0=−540 lb.⋅1.5 ft.+R
B
⋅6 ft.
Rewrite the equation to find the reaction force
R
B
=
540lb.⋅1.5 ft.
6 ft.
=135 lb.
Sum of the forces
∑
F
y
=0=R
A
−540 lb.+135 lb.
. Solve for the reaction force
R
A
=540 lb.−135 lb.=405 lb.
.
A cantilever beam with a single support has a reaction force and a reaction moment.
The reaction force R
B
equals the sum of the applied forces on the beam, so
R
B
=P=5 kips
.
The moment reaction equals the sum of the moments about point B – the applied load
times its distance from the wall – so
M
B
=P⋅x=5 kips⋅7 ft.=35kip ft.
.
65
5 kips
R
B
M
B
A B
7 ft.
A B
R
B
R
A
3 ft. 6 ft. 2 ft.
60 lb./ft.
=
A B
R
B
R
A
1.5 ft.
6 ft.
540 lb.
Load diagram Equivalent load diagram

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
When we calculate reaction forces and torques on tension members, torsion members,
and beams, we are calculating external forces and torques. Unless the material has no
strength at all, the material resists these external loads by developing internal loads.
Apply a torque of 25 ft.lb. to each end of a ½ inch diameter rod, and a resisting torque of
25 ft.lb. exists within the rod all along its length. Apply a tensile force of 400 N to each
end of a 2 cm diameter rod, and a resisting tensile force of 400N exists within the rod all
along its length. Beams in bending also develop internal forces to resist external forces.
Since the external forces on beams are transverse (perpendicular to the axis of the beam),
the internal resisting forces are also transverse forces.
Imagine a simply-supported beam with a point load at the mid-span. Cut the beam to the
left of the point load, and draw a free-body diagram of the beam segment. In a free-body
diagram, forces must balance. Therefore, a downward force at the cut edge balances the
support reaction R
A
. We call this shear force V. It is a shear force because the force acts
parallel to a surface (the cut edge of the beam).
The forces R
A
and V are in balance (equal in value; opposite in sign), but our segment
wants to spin clockwise about point A. To counteract this tendency to spin, a moment M
develops within the beam to prevent this rotation. The moment equals the shear force
times its distance from point A.
Cut the beam to the right of the point load, and draw the free-body diagram. Since P is larger than R
A
, force V points
upwards.
!*
Calculate the shear forces in this beam to the left and to the right of the 30 kN point
load.
The loading is symmetrical, so
R
A
=R
B
=
P
2
=
30 kN
2
=15 kN
.
Use the sum of the forces to find V.
Between support A and point load P,
∑
F
y
=0=R
A
−V
1
.
Solving for shear load,
V
1
=−R
A
=−15 kN
.
Between point load P and support B,
∑
F
y
=0=R
A
−P+V
2
.
Solving for shear load,
V
2
=−R
A
+P =−15 kN+30 kN=15 kN
.
66
30 kN
R
B
R
A
A B
4 m 4 m
V
1
R
A
A
M
R
A
A
M
V
2
P
P
R
B
R
A
A B
L/2 L/2
V
R
A
A
R
A
A
M
V
R
A
A
M
V
P

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
We can sketch V as a function of location along the beam using a
Shear Diagram. Draw vertical construction lines below the load
diagram wherever the applied loads and reactions occur. Draw a
horizontal construction line, indicating zero shear load. Next, draw the
value of V along the length of the beam, as follows:
% Starting at the left side of the shear diagram, go up 15 kN,
because R
A
is 15 kN upwards.
- There are no additional loads on the beam until you get to the
midspan, so the shear value remains at 15 kN.
. The applied load at the midspan is 30 kN downwards, therefore
the shear load is
15 kN−30 kN=−15 kN
.
2 There are no additional loads on the beam until you get to point
B, so the shear value remains at -15kN.
4 At point B, the reaction force R
B
= 15 kN upwards, therefore the
shear load is
−15 kN+15 kN=0
. If you don’t get to 0, you know you
made a mistake someplace.
Finish the shear diagram by shading the areas between your line and
the horizontal zero shear line. Mark all significant points (anywhere
the shear line changes direction). In the next chapter, we will use the
maximum absolute value of shear load,
∣
V
∣
max
, to calculate the
maximum shear stress in the beam.
A point load at the midspan of a simply-supported beam produces identical reaction forces and a symmetric shear diagram
with two rectangles. If the point load is not at the midspan, use sum of the moments and sum of the forces to calculate the
reaction forces. Draw vertical construction lines below the applied loads and reaction forces, draw a horizontal line at zero
shear, then draw the shear value along the length of the beam.
!"2
Draw a complete shear diagram for a simply-supported 8 ft. beam with a 100 lb.
point load 2 ft. to the right of point A.
Use sum of the moments and sum of the forces to find the reaction
forces R
A
and R
B
.
Starting the shear diagram at zero shear, go up
R
A
=75lb.
at point A. There are
no loads between point A and the applied point load, so the shear load does not
change. Draw a horizontal line to the right, until you reach the point load. Draw
a vertical line down 100 lb., reaching a value
V =−25lb.
There are no loads
between the point load and point B, so the shear load does not change.
Draw a horizontal line to the right, until you reach point B. The reaction force at B is 25 lb. upwards, so draw a vertical
line up 25 lb., reaching a value
V =0
. Again we have two rectangles, but they are not symmetric; the beam carries three
times as much shear load to the left of the point load than it does to the right.
67
30 kN
A B
4 m 4 m
15 kN
15 kN
15 kN
-15 kN
V
Step 5
15 kN
-15 kN
V
Finished
shear
diagram
15 kN
-15 kN
V
Step 4
15 kN
-15 kN
V
Step 3
15 kN
V
15 kN
V
Step 2
Step 1
100 lb.
A B
6 ft.
75 lb.
25 lb.
75 lb.
-25 lb.
V
2 ft.

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
Multiple point loads produce a stepped shear diagram.
!""
Draw a complete shear diagram for a simply-supported 8 ft. beam with 100 lb.
point loads every 2 ft. along the length.
The loading is symmetrical, so the reaction forces equal half the total
applied load.
Calculate the shear values as:
V
1
=R
A
=150lb.
V
2
=V
1
−100 lb.=50 lb.
V
3
=V
2
−100 lb.=−50lb.
V
4
=V
3
−100 lb.=−150 lb.
V
5
=V
4
+R
B
=−150lb.+150 lb.=0
In this problem,
∣
V
∣
max
=150 lb.
A uniformly distributed load is like an infinite number of small point loads along the length of the beam, so the shear
diagram is like a stepped multiple point load shear diagram with infinitely small steps.
!"#
Draw a complete shear diagram for a simply-supported 4 m beam with a
uniformly distributed load of 3 kN/m.
The loading is symmetrical, so the reaction forces equal half the total
applied load.
R
A
=R
B
=
W
2
=
wL
2
=
3 kN⋅4 m
m 2
=6 kN
.
A complete shear diagram includes the values of the shear at locations of
applied point loads and reaction forces.
V
1
=R
A
=6 kN
V
2
=V
1
−
3kN
m
4m
=−6kN
V
3
=V
2
+R
B
=−6 kN+6 kN=0
In this problem,
∣
V
∣
max
=6 kN
If the uniformly distributed load does not extend along the entire length of the beam, then draw an equivalent load diagram
to find the reaction forces. Go back to the original load diagram to draw the shear diagram; do not use the equivalent load
diagram to draw the shear diagram.
68
100 lb.
A B
150 lb. 150 lb.
V
1
=150 lb.
V
2 ft.
100 lb. 100 lb.
2 ft. 2 ft. 2 ft.
V
2
=50 lb.
V
3
= -50 lb.
V
4
= -150 lb.
A B
6 kN
6 kN
V
1
=6 kN
V V
3
= 0
V
2
= -6 kN
3 kN/m
4 m
Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
!"$
Draw a complete shear diagram for a simply-
supported 20 ft. beam which has a uniform
distributed load of 2 kips/ft. running from the
left end for 6 feet.
Draw an equivalent load diagram,
placing the equivalent load at the centroid of
the distributed load. Use the equivalent load
diagram to find the reaction forces.
The distributed load runs for 6 ft., so the
location of the equivalent load is 3 ft. from the
left end of the beam.
The equivalent load
W =wL=
2 kips⋅6ft.
ft.
=12 kips
.
The moment about point A is
∑
M
A
=0=−12 kips⋅3ft.+R
B
⋅20 ft.
.
Rewrite the equation to find the reaction force
R
B
=
12 kips⋅3 ft.
20 ft.
=1.8 kips
.
Sum of the forces
∑
F
y
=0=R
A
−12 kips+1.8 kips
. Solve for the reaction force
R
A
=12 kips−1.8 kips=10.2 kips
.
Draw construction lines down from the original load diagram wherever a point load or reaction exists, and wherever a
distributed load starts or stops. Calculate the shear loads at these points.
V
1
=R
A
=10.2 kips
V
2
=V
1
−
2 kips
ft.
6ft.
=−1.8 kips
V
3
=V
2
+R
B
=−1.8 kips+1.8 kips=0
∣
V
∣
max
=10.2kips
Multiple point loads of increasing load will give you an asymmetric stepped shear diagram.
!"%
Draw a complete shear diagram for a simply-supported 4 m beam which has a
three different point loads as shown in the load diagram.
Use sum of the moments and sum of the forces to find R
A
and R
B
.
Calculate the shear loads as follows:
V
1
=R
A
=250 N
V
2
=V
1
−100 N =150 N
V
3
=V
2
−200 lb.=−50 N
V
4
=V
3
−300 N=−350 N
V
5
=V
4
+R
B
=−350 N+350 N=0
In this problem,
∣
V
∣
max
=350 kN
A nonuniformly distributed load produces two different reaction forces. Draw an equivalent load diagram to find the
reaction forces. Go back to the original load diagram to draw the shear diagram. A wedge-shaped nonuniformly distributed
load is like an infinite number of small point loads of increasing magnitude along the length of the beam, so the shear
69
2 kips/ft.
R
B
R
A
A B
=
R
B
R
A
A B
Load diagram Equivalent load diagram
6 ft.
14 ft.
3 ft.
20 ft.
12 kips
V
1
=10.2 kips
V
V
3
= 0
V
2
= -1.8 kips
100 N
A B
250 N 350 N
V
1
=250 N
V
1m
200 N 300 N
1m 1m 1m
V
2
=150 N
V
3
= -50 N
V
4
= -350 N
V
5
= 0
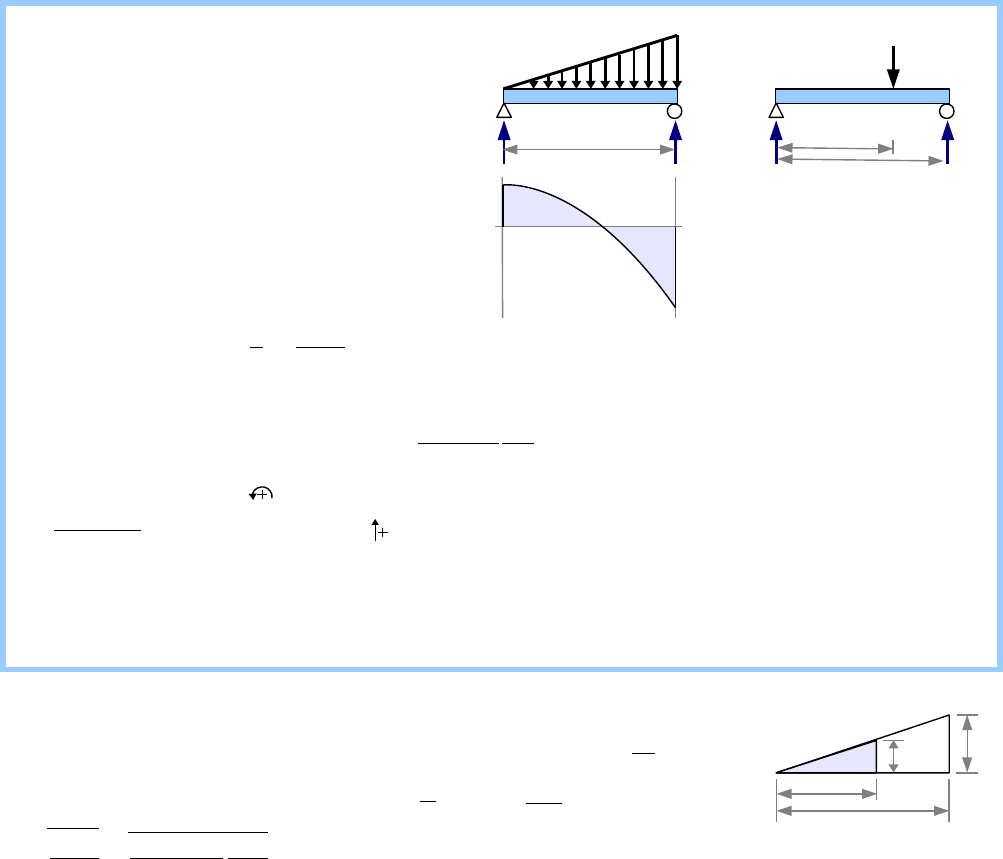
Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
diagram is like the previous stepped multiple point load shear diagram in which the slope of the curve increases
parabolically.
!"&
Draw a complete shear diagram for a simply-
supported 6 m beam which has a wedge-shaped
nonuniformly distributed load of 0 kN/m at the left
end of the beam to 5 kN/m at the right end of the
beam.
Draw an equivalent load diagram, placing
the equivalent load at the centroid of the
distributed load. The centroid of a triangle lies
two-thirds of the distance from the point of the
triangle. Use the equivalent load diagram to find
the reaction forces.
The centroid is located at
x=
2
3
L=
2⋅6 m
3
=4 m
,
measuring from the left end of the beam. The equivalent load is the average of the minimum and maximum distributed
loads times the length of the distributed load:
W =
(0+5) kN
2 m
6 m
=15 kN
.
The moment about point A is
∑
M
A
=0=−15 kN⋅4 m+R
B
⋅6 m
. Rewrite the equation to find the reaction force
R
B
=
15 kN⋅4 m
6 m
=10 kN
. Sum of the forces
∑
F
y
=0= R
A
−15 kN +10 kN
. Solve for
R
A
=15kN −10 kN=5 kN
.
Draw construction lines down from the original load diagram at the two reaction forces. Calculate the shear loads at these
points.
V
1
=R
A
=5 kN
V
2
=V
1
−15 kN=−10 kN
V
3
=V
2
+R
B
=−10 kN+10 kN=0
The shear line crosses the axis where the area of the distributed load equals R
A
. The area of
the distributed load is one half the base times the height of the triangle, or
a=
xh
2
. By
similar triangles, the height of the little triangle
h=
x
L
w
, so
a=
x
2
w
2 L
=R
A
. Solving,
x=
√
2 LR
A
w
=
√
2⋅6 m⋅5 kN m
5 kN
=3.46 m
. The shear line crosses the axis 3.46 m from the
left end of the beam.
Look at the shear diagrams, and you can see that point loads create rectangles, uniform distributed loads create triangles,
and wedge-shaped (triangular) distributed loads create parabolas.
Shear diagrams for cantilever beams follow the same rules as for simply supported beams. First, find the reactions; next,
draw the shear diagram using construction lines wherever a point load occurs or a distributed load starts or stops.
70
5 kN
A B
=
R
B
R
A
A B
Load diagram Equivalent load diagram
6 m
4 m
15 kN
6 m
V
1
=5 kN
V
V
2
= -10 kN
V
3
= 0
5 kN/m
10 kN
h
w
L
x
a

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
!"'
Draw a complete shear diagram for a 10 foot cantilever beam having a 5 kip
point load 7 feet from the wall.
Since there is no reaction force at the left end, there is no shear load
until we get to the applied load. Then, the shear load is negative (downward)
until we get to the support, where R
B
is positive (upward).
The moment about point B is
∑
M
B
=0=5 kips⋅7 ft.=35 kip ft.
. Sum of the
forces
∑
F
y
=0=R
B
−5 kips
therefore
R
B
=5 kips
.
Draw construction lines down from the original load diagram at the point load
and the reaction force. Calculate the shear loads at these points.
V
1
=P=−5 kips
V
2
=V
1
+5 kips=0
With a shear diagram, we can identify the location and size of the largest shear load in a beam. Therefore, we know the
location of the largest shear stress, and we can calculate the value of this stress. Once we know the actual stress in the
material, we can compare this values with the shear strength of the material, and we can know whether the beam will fail in
shear. Shear diagrams are necessary for drawing bending moment diagrams (“moment diagrams”, for short), which we can
use to identify the location and size of bending stresses that develop within beams. We can compare the actual bending
stresses with the yield strength of the material, and we can know whether the beam will fail in bending.
71
5 kips
R
B
M
B
A B
7 ft.
V
V
3
= -50 N
V
1
= -5 kips
V
2
= 0
10 ft.
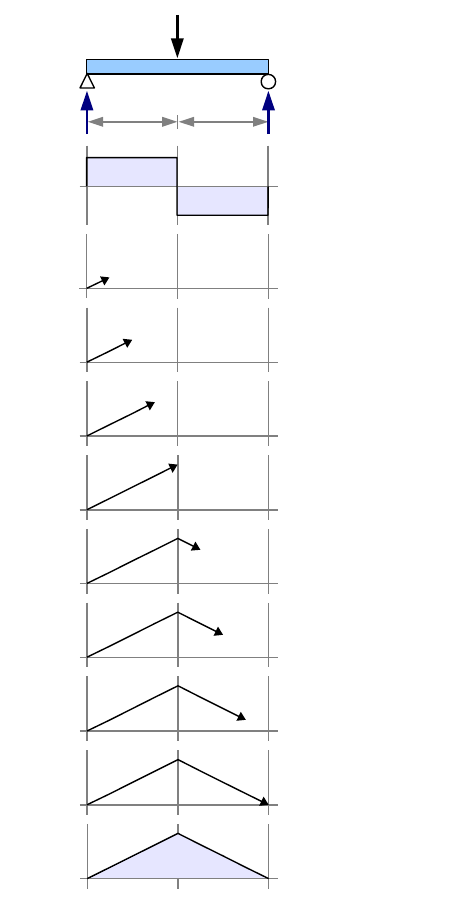
Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
'
The moment about a point along a beam is defined as the
distance from that point to a force acting perpendicular to
the beam, so the units are force × distance:
lb.⋅ft.
(or
ft.⋅lb.
– the order does not matter),
lb.⋅in.
,
kip⋅ft.
,
N⋅m
,
or
kN⋅m
. We can graph the value of the bending moment
along a beam by drawing a moment diagram.
To draw a moment diagram, sketch the value of the moment
produced by the shear force V times the distance from the
left end of the beam. At the first meter, V = 15 kN, so
moment
M
1
=15 kN×1m=15 kN⋅m
.
At 2 m,
M
2
=M
1
+15 kN×1 m=30 kN⋅m
At 3 m,
M
3
=M
2
+15 kN×1 m=45 kN⋅m
At 4 m,
M
4
=M
3
+15 kN×1 m=60 kN⋅m
At 5 m,
M
5
=M
4
−15 kN×1 m=45 kN⋅m
At 6 m,
M
6
=M
5
−15 kN×1 m=30 kN⋅m
At 7 m,
M
7
=M
6
−15 kN×1 m=15 kN⋅m
At 8 m,
M
8
=M
7
−15 kN×1 m=0 kN⋅m
Shade the finished diagram, marking all significant points
(places where the moment line changes direction). The most
important point is the maximum absolute value of M; this is
where the maximum bending stress occurs in the beam.
The value of the moment diagram at any point equals the
area of the shear diagram up to that point. The shear
diagram has positive areas above the zero line, and negative
areas below the zero line. When the shear area is positive,
the moment increases; when the shear area is negative, the
moment decreases.
You can draw the moment diagram faster by calculating the
area of the left-hand rectangle in the shear diagram:
M
max
=15 kN×4 m=60 kN⋅m
. Verify that
M
8
=0
by
subtracting the area of the second rectangle in the shear
diagram:
M
8
=M
max
−15 kN×4 m=0 kN⋅m
.
72
30 kN
A B
4 m 4 m
15 kN 15 kN
-15 kN
Finished moment
diagram with max.
labeled
M
1
M
15 kN
V
Moment at
x = 1 m
Shear
diagram
M
M
M
M
M
M
M
8
M
M
max
= 60 kN∙m
M
M
7
M
6
M
5
M
4
M
3
M
2
Moment at
x = 2 m
Moment at
x = 3 m
Moment at
x = 4 m
Moment at
x = 5 m
Moment at
x = 6 m
Moment at
x = 7 m
Moment at
x = 8 m
Load
diagram

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
It is a good idea to check the moment at point B. If you end up with a value other
than 0, then you know there is a mistake someplace. Most likely, the error is in
the reaction forces. You can draw a shear diagram that works with the wrong
reaction forces, but you cannot draw a good moment diagram if R
A
and R
B
are
wrong. This is an amazing feature of moment diagrams – they tell you if your
solution is right!
If the point load is not at the midspan, then the maximum moment will also be
offset. In this example, the maximum moment is the area of the shear diagram up
to the point load:
M
max
=R
A
⋅L
1
.
Multiple point loads will give you multiple rectangles on the shear diagram, and
multiple triangles on the moment diagram.
!"(
Draw complete shear and moment diagrams for an 8 foot long, simply-
supported beam having 100 lb. point loads every 2 feet.
The loading is symmetrical, therefore the reaction forces R
A
and R
B
are each equal to half the total applied load.
R
A
=R
B
=(100lb.+100 lb.+100lb.)/ 2=150lb.
Draw construction lines down from the load diagram at each reaction force
and applied load. The shear diagram is a series of rectangles.
Calculate the values on the moment diagram as follows:
M
1
=2ft.×150lb.=300 ft.⋅lb.
M
2
=M
1
+2ft.×50 lb.=400ft.⋅lb.
M
3
=M
2
−2ft.×50 lb.=300 ft.⋅lb.
M
4
=M
3
−2 ft.×150 lb.=0ft.⋅lb.
A uniformly distributed load produces a parabolic moment diagram. Close to point A, a large shear produces a steep slope
in the moment diagram. As you approach the midspan, the smaller shear produces a shallower slope in the moment diagram.
Beyond the midspan, an increasingly negative shear produces an increasingly steeper slope downwards.
The maximum moment equals the area of the left-hand triangle. Subtract the area of the right-hand triangle to get the
moment at point B.
73
100 lb.
A B
150 lb.
150 lb.
V
1
=150 lb.
V
2 ft.
100 lb. 100 lb.
2 ft. 2 ft. 2 ft.
V
2
=50 lb.
V
3
= -50 lb.
V
4
= -150 lb.
M
1
=300 ft.lb.
M
M
4
= 0 ft.lb.
M
2
=400 ft.lb.
M
3
=300 ft.lb.
P
A B
L
1
R
A
V
M
max
M
R
B
R
A
L
2
R
B

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
!")
Draw complete shear and moment diagrams for an 8 meter long, simply-
supported beam having a uniform distributed load of 3 kN/m.
The loading is symmetrical, therefore the reaction forces R
A
and R
B
are each equal to half the total applied load.
R
A
=R
B
=
3kN
m
8 m
2
=12 kN
Draw construction lines down from the load diagram at each reaction force .
The shear diagram is two triangles. Draw a construction line down from
where the shear line crosses the zero axis.
The max. moment is equal to the area of the left-hand triangle: the base times
the height divided by 2. The base of the triangle is half the beam length, 4 m.
M
max
=
12 kN×4 m
2
=24 kN⋅m
The moment at point B is the moment at the
midspan minus the area of the right-hand triangle.
M
B
=M
max
−
12 kN×4 m
2
=0 kN⋅m
We’ve seen that a nonuniform wedge-shaped distributed load produces a parabolic shear diagram. The moment diagram
looks like a parabola skewed to the right, with the maximum moment at the point where the shear diagram crosses the zero-
load axis.
74
A B
12 kN
12 kN
V
1
=12 kN
V V
3
= 0
V
2
= -12 kN
3 kN/m
8 m
M
max
=24 kN∙m
M

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
!"*
Draw complete shear and moment diagrams for a
12 foot long, simply-supported beam having a
wedge-shaped nonuniform distributed load of 0
lb./ft. at the left end of the beam and 300 lb./ft. at
the right end of the beam.
Draw an equivalent load diagram, placing
the equivalent point load at the centroid of the
distributed load. The centroid of a triangle lies 2/3
of the distance from the tip of the triangle. Use the
equivalent load diagram to find the reaction forces.
The centroid of the triangular load profile lies at
x=
2
3
L=
2⋅12 ft.
3
=8ft.
, measuring from point A.
The equivalent load is the average of the minimum
and maximum distributed loads times
the length of the distributed load:
W =
(0+300)lb.
2 ft.
12 ft.
=1800 lb.
The moment about point A is
∑
M
A
=0=−1800 lb.⋅8ft.+R
B
⋅12ft.
. Rewrite the equation to find the reaction force
R
B
=
1800 lb.⋅8ft.
12 ft.
=1200 lb.
Sum of the forces
∑
F
y
=0=R
A
−1800 lb.+1200 lb.
Solve for
R
A
=1800lb.−1200lb.=600 lb.
Draw construction lines down from the original load diagram at the two reaction forces. Calculate the shear loads at these
points.
V
1
=R
A
=600 lb.
,
V
2
=V
1
−1800 lb.=−1200 lb.
,
V
3
=V
2
+R
B
=−1200 lb.+1200 lb.=0
Draw a construction line down from the shear diagram where the shear line crosses the zero axis – this construction line
marks the location of the max. moment. We need to find the location of this point in order to calculate the max. moment.
Consider that the value of V at any point along the shear diagram equals the reaction force
R
A
minus the area of the distributed load, a
w
:
V = R
A
−a
w
. The area of the triangle-shaped
distributed load at any point equals one-half the base times the height of the triangle. Let
the base be x, the distance from the left end of the beam. The height is a fraction of the
distributed load w at point B. By similar triangles,
height=
x
L
w
, so area
a
w
=
1
2
x
x
L
w=
x
2
w
2 L
and shear force
V =R
A
−
x
2
w
2 L
. Where the shear line crosses the zero
line,
V =0
, therefore
x=
√
2 L R
A
w
=
√
2⋅12ft.⋅600 lb. ft.
300 lb.
=6.928 ft.
The maximum moment is equal to the area of the shear diagram to the left of this
construction line. Since the shear diagram is a parabola, the area of the shear diagram to
the left of the construction line is 2/3 of the base of the parabola times its height.
M
max
=a
V
=
2
3
V
1
x=
2⋅600lb.⋅6.928 ft.
3
=2770 ft.⋅lb.
So far, all of the examples have shown moment diagrams with positive areas. A cantilever beam with a point load has a
negative area in the moment diagram.
75
600 lb.
A B
=
R
B
R
A
A B
Load diagram Equivalent load diagram
12 ft.
8 ft.
1800 lb.
12 ft.
V
1
=600 lb.
V
V
2
= -1200 lb.
V
3
= 0
300 lb./ft.
1200 lb.
M
max
M
R
A
x
V
1
=R
A
V
M
max
M
x
L
w
A
a
V
a
w

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
!#2
Draw complete shear and moment diagrams for a cantilever beam having a
point load of 5 kips, located 7 feet from the wall.
By inspection, the reaction force
R
B
=5 kips
. The reaction moment
M
B
=5 kips×7ft.=35 kip⋅ft.
The shear diagram is a rectangle, so the moment
diagram will be a triangle. The area of the shear diagram equals the value of
the moment diagram, so
M
1
=−5 kips×7 ft.=−35kip⋅ft.
M
2
=−35 kip⋅ft.+M
B
=0 kip⋅ft.
In this problem,
∣
M
∣
max
=35 kip⋅ft.
The shear diagram of a cantilever beam with a uniform distributed load is a triangle. Use an equivalent load diagram to find
the reaction force and reaction moment, then draw shear and moment diagrams below the original load diagram.
!#"
Draw complete shear and moment diagrams
for a 3 m long cantilever beam having a
uniform distributed load of 2 kN/m along its
length.
Draw an equivalent load diagram,
placing the equivalent point load at the
centroid of the distributed load. The centroid
of a rectangle lies at the halfway point. Use
the equivalent load diagram to find the
reaction force and reaction moment.
R
B
=
2 kN
m
3 m
=6 kN
M
B
=6 kN×1.5 m=9 kN⋅m
The shear diagram is a triangle, so the moment diagram is a parabola with
∣
M
∣
max
=9 kN⋅m
.
Follow the same procedures to draw the shear and moment diagrams of an overhanging beam with a distributed load and a
two point loads.
76
5 kips
R
B
M
B
A B
7 ft.
V
V
3
= -50 N
V
1
= -5 kips
V
2
= 0
10 ft.
M
M
1
= -35 kip∙ft.
M
2
= 0
2 kN/m
R
B
A B
=
R
B
A B
Load diagram
Equivalent load diagram
3 m
1.5 m
6 kN
V
V
2
= 0
V
1
= -6 kN
M
B
M
B
M M
2
= 0
M
1
= -9 kN∙m

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
!##
Draw complete shear and
moment diagrams for a 36 foot
long overhanging beam having
a uniform distributed load and
two point loads as shown.
Draw an equivalent
load diagram, placing the
equivalent point load at the
centroid of the distributed load,
which is 9 ft. from point A.
Use the equivalent load diagram
to find the reaction forces, then
draw the shear and moment
diagrams below the original
load diagram.
R
B
=
36 kips⋅9 ft.+12 kips⋅18 ft.+10 kips⋅36ft.
30 ft.
=30 kips
,
R
A
=36 kips+12 kips+10 kips−30 kips=28 kips
Calculate the shear values:
V
1
=R
A
=28 kips
,
V
2
=V
1
−
2 kips
ft.
18 ft.
=−8 kips
,
V
3
=V
2
−12 kips=−20 kips
,
V
4
=V
3
+30 kips=10 kips
,
V
5
=V
4
−10 kips=0 kips
The moment curve starts with a parabola going up until the shear curve crosses zero; once the shear is negative, the
moment curve drops parabolically until the end of the distributed load. In order to calculate the moment values, we need to
know where the shear curve crosses the zero line. Use similar triangles to find x, then calculate the area of the left-hand
triangle in the shear diagram:
x=18ft.
28 kips
36 kips
=14 ft.
The area of the left-hand triangle is
M
1
=
28 kips⋅14 ft.
2
=196 kip⋅ft.
Subtract the area of the right-hand triangle to find
M
2
=M
1
−
8 kips⋅4ft.
2
=180 kip⋅ft.
Subtract the lower rectangle to find
M
3
=M
2
−20 kips⋅12 ft.=−60 kip⋅ft.
Add the
upper rectangle to find
M
4
=M
3
+10 kips⋅6ft.=0 kip⋅ft.
In this problem,
∣
M
∣
max
=196 kip⋅ft.
77
x
18 ft.
28 kips
36 kips
2 kips/ft.
R
B
R
A
A B
=
Load diagram
18 ft. 12 ft.
V
1
=28 kips
V
V
4
= 10 kips
V
5
= 0 kips
10 kips
12 kips
6 ft.
R
B
R
A
A B
Equivalent load diagram
9 ft.
30 ft.
10 kips
12 kips
36 ft.
36 kips
18 ft.
V
2
= -8 kips
V
3
= -20 kips
M
M
3
M
4
M
2
M
1

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
!#$
Draw complete shear and moment diagrams for a 12 meter long overhanging beam having a uniform distributed load and
two nonuniform distributed loads.
Draw an equivalent load
diagram, placing the equivalent point
loads at the centroids of the
distributed loads (two triangular
distributed loads and one rectangular
distributed load).
Use the equivalent load diagram to
find the reaction forces, then draw
the shear and moment diagrams
below the original load diagram.
The equivalent loads are
2 kN
m
3m
2
=3 kN
,
2 kN
m
5m
=10 kN
, and
2 kN
m
4 m
2
=4 kN
.
R
B
=
−3kN⋅1 m+10 kN⋅2.5 m+4 kN⋅6.33 m
9 m
=5.26 kN
,
R
A
=3 kN+10 kN+4 kN−5.26 kN=11.74 kN
The shear diagram goes downward as a concave second-degree parabola under the nonuniform distributed load, straight up
at R
A
, downward at a diagonal under the uniform distributed load, then downward as a convex second-degree parabola
under the nonuniform distributed load, and straight up at R
B
.
Calculate the shear values:
V
1
=
−2 kN
m
3m
2
=−3 kN
,
V
2
=V
1
+R
A
=8.74 kN
,
V
3
=V
2
−
2 kN
m
5m
=−1.26 kN
,
V
4
=V
3
−
−2kN
m
4 m
2
=−5.26 kN
,
V
5
=V
4
+R
B
=0 kN
The moment curve goes downward as a concave third-degree parabola. To find the
value of M
1
, calculate the area under the concave second-degree parabola at the
left end of the shear diagram. From Appendix C, the area under a concave second-
degree parabola is
b h
3
. The base is 3 m, and the height is -3 kN. Therefore
M
1
=
−3 kN⋅3m
3
=−3 kN⋅m
In order to calculate M
2
, we need to know where the shear curve crosses the zero
line. Use similar triangles to find x, then calculate the area of the left-hand triangle
in the shear diagram:
x=5m
8.74 kN
10 kN
=4.37 m
78
2 kN/m
R
B
R
A
A B
=
Load diagram
3 m
V
1
= -3 kN
V
V
4
= -5.26 kN
V
5
= 0 kN
Equivalent load diagram
6.33 m
10 kN
9 m
3 kN
2.5 m
V
2
= 8.74 kN
V
3
= -1.26 kN
M
M
3
M
4
M
2
M
1
5 m 4 m
R
B
R
A
A B
1 m
4 kN
x
5 m
8.74 kN
10 kN

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
!#$
M
2
=M
1
+
8.74 kN⋅4.37m
2
=16.1 kN⋅m
The base of the small triangle in the shear diagram is 5 m – 4.37 m = 0.63 m.
M
3
=M
2
−
1.26kN⋅0.63 m
2
=15.7kN⋅m
Although it is tempting to assume that
M
4
=0 kN⋅m
to finish the moment
diagram, it's best to calculate it, to be sure that there are no errors in the reaction
force calculations.
The rightmost segment in the shear diagram is a rectangle and a convex second
degree parabola. From Appendix C, the area of a convex second degree parabola
is
2 b h
3
.
M
4
=M
3
−1.26 kN⋅4 m−
2⋅4 m⋅4 kN
3
=0 kN⋅m
In this problem,
V
max
=8.74 kN
and
M
max
=16.1kN⋅m
Some engineering solutions require an algebraic solution. Imagine you are designing a set of beams using the same general
loading case, but the loads change from one case to the next. If you can develop an algebraic solution, then you can plug in
the numbers for each case (perhaps with a computer program) instead of solving every case from scratch. Example #24
shows how to create shear and moment diagrams for an algebraic problem.
79
4.37 m
5 m
8.74 kN
10 kN
0.63 m
-5.26 kN
-1.26 kN
4 m
4 kN

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
!#%
Draw complete algebraic shear and moment diagrams for an overhanging beam loaded as shown.
Draw an equivalent load diagram, placing
the equivalent point load at the centroid of the
distributed load.
Use Sum of the Moments and Sum of the Forces to
find the reactions at points A and B.
R
B
=
−P a+w b⋅0.5 b
b
=
−P a
b
+
w b
2
R
A
=P+w b− R
B
=P +
P a
b
+
w b
2
V
1
=−P
V
2
=V
1
+R
A
=
P a
b
+
w b
2
V
3
=V
2
−w b=
P a
b
−
w b
2
V
4
=V
3
+R
B
=0
M
1
=−V
1
a=−P a
Use Similar Triangles to determine the base of the upper triangle. The overall height is
the weight per unit length times the distance it acts upon, bw.
x=b
V
2
b w
=
V
2
w
=
P a
b
+
w b
2
w
=
P a
b w
+
b
2
M
2
=M
1
+
V
2
x
2
=−P a+
(
P a
b
+
w b
2
)(
P a
b w
+
b
2
)
2
=
P
2
a
2
2b
2
w
−
P a
2
+
w b
2
8
The base of the lower triangle is
b−x=b−
(
P a
b w
+
b
2
)
=
b
2
−
P a
b w
M
3
= M
2
+
V
3
(b−x)
2
= M
2
+
(
P a
b
−
w b
2
)(
b
2
−
P a
b w
)
2
= M
2
+
P ab
2 b
−
P
2
a
2
b
2
w
−
w b
2
4
+
P a b w
2b w
2
= M
2
+
P a
2
−
P
2
a
2
b
2
w
−
w b
2
4
+
P a
2
2
=
P
2
a
2
2 b
2
w
−
P a
2
+
w b
2
8
+
P a
2
−
P a
2
2b
2
w
−
w b
2
8
= 0
We do not know in advance whether
M
max
=M
1
or
M
max
=M
2
...it depends on the values of a, b, w, and P.
80
A B
=
Load diagram Equivalent load diagram
b
V
1
V
V
4
= 0
M
R
B
R
A
w
P
a
A B
b
R
B
R
A
a
P wb
0.5b
V
2
V
3
M
1
M
2
M
3
= 0
x
b
V
2
bw

Chapter 8: Beam Reactions, Shear Diagrams, and Moment Diagrams
In summary, the value of
the moment diagram at a
given point equals the area
of the shear diagram up to
that point. The slope of
the moment diagram at a
given point equals the
value of the shear load at
that point.
Load type Shear diagram shape Moment diagram shape
Point Rectangles Triangles
Uniform distributed Triangles Parabolas (second degree)
Wedge-shaped nonuniform distributed Parabolas (second degree) Parabolas (third degree)
+,
Use
∑
M
A
=0
and
∑
F
y
=0
to find reaction forces for simply-supported beams.
Use
∑
M
support
and
∑
F
y
=0
to find the reaction moment and reaction force for cantilever beams.
81

Chapter 9: Stresses in Beams
>&
In the last chapter, we learned how to draw shear and bending moment
diagrams for beams. These diagrams tell us the location and magnitude
of the maximum shear load and maximum bending moment. We can use
V
max
and M
max
to calculate the maximum shear stress and max. bending
stress in a beam, then we can compare these results with the allowable
shear stress and bending stress of the material. If the actual value is less
than the allowable value, then the beam is safe; if the actual value is
greater than the allowable, then we need to select a different beam.
A point load at the midspan of a beam makes the beam bend. We can
sketch a deflection diagram to show this bending. The deflection
diagram shows the beam as if it had no depth, because it is easier to
draw a curve than to draw a double curve with shading. A real beam has
depth, and when it is bent, the top surface shortens while the bottom
surface lengthens...the top surface has a negative strain, while the
bottom surface has a positive strain. Plot strain vs. depth: the strain
varies linearly from top to bottom, and is zero at the centroidal axis.
We saw in Chapter 2 that materials like steel and
aluminum follow Hooke's law: the ratio of stress/strain
is Young's modulus, a constant. Therefore, the stress in
the beam also varies linearly from top to bottom, and is
zero at the centroidal axis of the beam. We call this
axis the neutral axis, where stress is zero.
9
This
bending stress acts perpendicular to the cross-sectional
area of the beam, so the stress is a normal stress; it is
negative on the top and positive on the bottom.
We can calculate the bending stress at any position y
from the neutral axis: the stress is proportional to the
distance from the neutral axis, so
σ=σ
max
y
c
where c
is the distance from the neutral axis to the surface of
the beam. This is the same meaning of c that we used
in torsion problems.
Think about a very small area a at a distance y from the neutral axis. Since stress is force divided by area, the force acting
on this area is equal to the stress times the area:
P=σ⋅a=
σ
max
a y
c
. The moment of this force with respect to the neutral
axis is
M =P⋅y=
σ
max
a y
2
c
. If we sum up the moment for all values of a and y,
M =
σ
max
c
∑
1
n
a
i
y
i
2
. Recall from Chapter 5,
the moment of inertia of a cross-sectional area relative to the x-x centroidal axis is
I
x
=
∑
1
n
a
i
y
i
2
, therefore
M =
σ
max
I
x
c
.
Rewrite this equation to solve for bending stress at the surface:
σ=
Mc
I
x
. This equation is called the Flexure Formula.
9 The centroidal axis and the neutral axis are the same if the beam is made of a single material that obeys Hooke's law. The centroidal
and neutral axes are often different in beams made of composite materials, like steel-reinforced concrete, or glass/epoxy composite.
82
P
A B
L/2 L/2
R
A
R
B
Moment
diagram
V
Shear
diagram
M
max
M
Load
diagram
V
max
Deflection
diagram
Δ
Δ
max
V
max
+ε
max
–ε
max
neutral axis
+σ
max
–σ
max
+σ
max
–σ
max
σ
yc
a
Side views of the beam
End view

Chapter 9: Stresses in Beams
We can use the moment equation if we want to know how much bending moment the beam can support. The allowable
moment
M
allowable
=
σ
allowable
I
x
c
.
!"
A 4×6 timber beam, 8 feet long, is loaded with a uniform distributed load of
54.65 lb./ft. The beam itself has a weight per unit length of 5.35 lb./ft. What
is the maximum bending stress, and where does it occur? Report the answer
in psi.
The total uniform distributed load is the applied load plus the weight
of the beam,
w
total
=w
applied
+w
weight
=
54.65lb.
ft.
+
5.35 lb.
ft.
=
60 lb.
ft.
The load is symmetrical, so the reaction forces are equal to half of the applied
load.
R
A
=R
B
=
W
2
=
wL
2
=
60lb.
ft.
8ft.
2
=240 lb.
The maximum moment equals the area of the left-hand triangle in the shear
diagram: one half the base times the height.
M
max
=
240lb.⋅4 ft.
2
=480 ft.⋅lb.
From Appendix E, the dimensions of a 4×6 timber are 3.5"×5.5". Since the cross-section is a rectangle, the moment of
inertia is
I
x
=
bh
3
12
=
3.5 in.(5.5 in.)
3
12
=48.53 in.
4
The value of c is
c=
h
2
=
5.5 in.
2
=2.75 in.
The maximum bending stress
occurs at the midspan, and is
σ=
Mc
I
x
=
480ft.⋅lb.(2.75 in.)
48.53in.
4
∣
12 in.
ft.
=326 psi
. Bending stress diminishes to zero at the ends.
What happens if you use the nominal dimensions instead of actual dimensions for the timber?
I
x
=
4in.(6 in.)
3
12
=72in.
4
,
c=
6in.
2
=3in.
, and
σ=
480ft.⋅lb.(3 in.)
72in.
∣
12in.
ft.
=240 psi
, which is 26% lower than the actual stress.
Tables in the Appendix list values for I
x
and I
y
for many shapes, but no values for c. Instead, the tables give the section
modulus, defined as
S
x
=
I
x
c
and
S
y
=
I
y
c
. Section modulus makes the stress calculation easier, because it combines two
terms into one. Bending stress
σ=
Mc
I
x
=
M
S
x
, and allowable moment
M
allowable
=
σ
allowable
I
x
c
=σ
allowable
S
x
.
In Example #1, the section modulus of a 4×6 timber is 17.6 in.
3
. Bending stress is
σ=
M
S
x
=
480 ft.⋅lb.
17.6 in.
3
∣
12in.
ft.
=327 psi
.
83
A B
240 lb.
240 lb.
V
1
=240 lb.
V V
3
= 0
V
2
= -240 lb.
w
applied
8 ft.
M
max
= 480 ft.∙lb.
M
w
weight

Chapter 9: Stresses in Beams
Simple shapes like rectangles and circles are symmetrical
about the neutral axis, so the distance c from the neutral axis
to the top surface is the same as the distance c from the
neutral axis to the bottom surface. Compound shapes like a
are not symmetrical about the x-x neutral axis, so there are
two values to consider: c
top
and c
bottom
. From the flexure
formula,
σ=
Mc
I
x
, the largest stress occurs on the surface
with the largest value of c. In the case of a -shaped beam
loaded on the top flange as shown, the largest stress is the
tensile stress along the bottom surface of the beam:
σ=
M c
bottom
I
x
.
!#
What is the allowable moment of a 2×4 Douglas fir beam? Report the answer in ft.⋅lb.
The allowable moment is the largest bending moment that a beam can support. From Appendix E, the section
modulus of a 2×4 timber is 3.06 in.
3
, and the allowable bending stress is 900 psi.
The allowable moment is
M
allowable
=σ
allowable
S
x
=
900 lb.
in.
2
3.06in.
3
∣
ft.
12in.
=230 ft.⋅lb.
(,+
Stress-strain diagrams for
many materials are
simplified as a cartoon
showing a straight line
segment for elastic
behavior followed by an
arc for plastic behavior. In
the elastic zone, stress is
proportional to strain; the
ratio is Young's modulus
E =
σ
ε
.
Almost all equations in this book apply only to the elastic zone. In the plastic zone, the stress required to stretch the material
increases due to strain hardening (also called work hardening) until the stress reaches a peak at the tensile strength of the
material. After the peak, the material begins to thin, and the cross-sectional area shrinks, so there is less material to support
the load, and eventually the material breaks.
84
c
c
c
bottom
c
top
c
c
End view
Side view
P
Stress
σ
plastic zoneelastic zone
Strain ε
σ
YS
σ
TS
Stress
σ
Strain ε
plastic zone
ε
Y
ε
P
σ
YS
strain hardening
elastic zone
Wood, concrete,
titanium, aluminum,
alloy steels, etc.
Low-carbon
steels only

Chapter 9: Stresses in Beams
Low-carbon steel used
for wide-flange beams
has an elastic zone
followed by a horizontal
plastic zone in which
the stress does not
change, so there is no
strain hardening. The
stress-strain curve for
low-carbon sheet steel
in Chapter 2 shows this
effect clearly. As the strain builds up, eventually strain
hardening begins, and the stress-strain curve arcs upwards. In
steel beam design, we can use the horizontal part of the
stress-strain curve to extend the load-carrying capacity of the
beam. Let's look at the strain and stress profiles in a steel
beam as the load is increased:
B% Strain and stress are in the elastic zone. They are
both zero at the neutral axis, and we have maximum
compressive and tensile values at the top and bottom
surfaces.
B- Strain and stress have reached the yield point, so
ε
2
=ε
Y
and
σ
2
=σ
YS
, the yield strength of the material.
B. Strain continues to increase, but the stress does not exceed the yield strength. Material below the surface reaches
the yield point, down to a certain depth. Below this depth, the interior bending stress remains in the elastic zone.
B2 Strain continues to increase. More of the material below the surface reaches the yield point, but the core is in the
elastic zone.
B4 Strain reaches the point of strain hardening,
ε
5
=ε
P
. All of the material has reached the yield point, becoming fully
plastic. Any additional load on the beam will cause the beam to fail by bending at this location, like two hinged bars.
We can draw an equivalent load diagram for the
fully-plastic beam at Point #5. The compressive
force acting above the neutral axis equals the yield
strength times the cross-sectional area of the beam
in compression (the area above the neutral axis):
P
C
=σ
YS
⋅A
C
. Likewise, the tensile force below
the neutral axis is
P
T
=σ
YS
⋅A
T
. The beam
develops an internal moment to counteract these
forces, equal to each force times the distance from
the neutral axis of the beam to the centroidal axis of each area. Since this moment is
counteracting fully-plastic loading, we call it the plastic moment, M
P
., given as
M
P
=P
C
y
C
+P
T
y
T
=σ
YS
A
C
y
C
+σ
YS
A
T
y
T
.
If we define a new variable
Z =A
C
y
C
+A
T
y
T
, then
M
P
=σ
YS
Z
. This new variable is the
sum of the first moments of the areas above and below the neutral axis; we call it the plastic
section modulus. Like section modulus, S, the plastic section modulus is calculated with
reference to either the x-x or the y-y neutral axis. The example in the diagram is Z
x
. Beams
loaded in the strong direction will use Z
x
; beams that are either loaded from the side or tipped on the side will use Z
y
.
85
+ε
1
–ε
1
neutral axis
+σ
1
–σ
1
#1
Stress
σ
Strain ε
ε
Y
ε
P
σ
YS
1 2 3 4 5
+ε
2
–ε
2
+σ
YS
–σ
YS
#2
+ε
3
–ε
3
+σ
YS
–σ
YS
#3
+ε
4
–ε
4
+σ
YS
–σ
YS
#4
+ε
5
–ε
5
+σ
YS
–σ
YS
#5
Strain profile
Stress profile
Stress profile
+σ
YS
–σ
YS
=
Equivalent load profile
End view
P
T
P
C
centroid of
top half
centroid of
bottom half
y
T
y
C
area A
C
area A
T

Chapter 9: Stresses in Beams
We can easily calculate Z for simple shapes; you can find Z
x
and Z
y
for complex shapes like wide-flanged beams in the
Appendix.
0 Each area is half the area of the rectangle. Each
moment arm is half the height of each area, or a quarter of the
height of the entire rectangle.
A
C
=A
T
=bh/2
y
C
= y
T
=h /4
Z
x
=A
C
y
C
+A
T
y
T
=
bh
2
h
4
+
b h
2
h
4
=
bh
2
4
and Z
y
=
h b
2
4
Each area is half the area of a circle. Find the moment arm in the Appendix.
A
C
=A
T
=
π d
2
4
×
1
2
=
π d
2
8
,
y
C
= y
T
=
2 d
3 π
, and
Z
x
=Z
y
=A
C
y
C
+A
T
y
T
=
π d
2
8
2 d
3 π
+
π d
2
8
2 d
3 π
=
d
3
6
While ideal beams follow the ideal stress-strain curves in the preceding section, real beams vary in strength due to defects in
manufacturing and handling. AISC recommends using a factor of safety of 1.67 in steel beam design, so
σ
allowable
=
σ
YS
1.67
=0.6σ
YS
. If we let the moment in a beam equal the plastic moment, then
M
allowable
=σ
allowable
Z =0.6 σ
YS
Z
.
!$
What is the allowable moment of a W200×59 wide-flange beam? Report the answer in kN∙m.
From Appendix D, the plastic section modulus is 652×10
3
mm
3
. From Appendix B, the yield strength is 345
MPa.
The allowable moment is
M
allowable
=0.6 σ
YS
Z
x
=
0.6 345 MPa 652×10
3
mm
3
∣
m
3
(10
3
mm)
3
∣
10
3
kN
MPa m
2
=135 kN⋅m
The bending stress in a low-carbon steel beam is
σ=
M
Z
x
.
86
h/4
h
b
h/4
d
2d / 3π
2d / 3π

Chapter 9: Stresses in Beams
Bending stress is a normal stress, acting perpendicularly to the
cross-sectional area of the beam. Apply a downward load on top
of a simply-supported beam, and the bending stress on the top
surface is horizontal and compressive; along the bottom surface it
is horizontal and tensile.
Beams also have a horizontal shear stress which acts parallel to
the neutral axis of the beam. Take a deck of playing cards and
flex it in your hand; the cards slide past each other. Think of this
sliding as strain; if the cards had been glued together, then a
corresponding shear stress would have developed in the adhesive.
Glue all but one of the cards on their faces, then place the free
card on top of the glued deck. Bend the deck, and the top card
slides very little with respect to the rest of the deck. Now take a
second deck having the same number of cards as the first deck,
and glue all of the cards in the second deck together. Place one
deck on the other and bend them; the two decks slide with respect
to each other – more so than if the decks were different
thicknesses. This experiment shows that the shear stress is zero at
the surface of a beam, and maximum at the neutral axis.
Bend a simply-supported beam with a point load at the midspan,
and the moment diagram is an isosceles triangle. Select two
points on the beam that are separated by a small distance Δx. On
the moment diagram,
M
1
<M
2
. Since bending stress is
proportional to bending moment,
σ
1
<σ
2
. Pick a horizontal plane
within the beam where you want to calculate the shear stress. In
this example, the shear plane is above the neutral axis. The cross-
sectional area between the shear plane and the top of the beam is
A'.
Draw a free-body diagram of the beam above the shear plane. The
horizontal force acting on this area at point 1 is
P
1
=σ
1
A'
.
Likewise, the horizontal force acting on this area at point 2 is
P
2
=σ
2
A '
. Since
σ
1
<σ
2
,
P
1
<P
2
. The sum of the forces in
the x direction equals zero, so the difference between these forces
is a horizontal shear force,
V
H
=P
2
−P
1
.
The normal stress acting on area A' at point 1 varies with depth: it
is highest on the top surface of the beam, and lower at the shear
plane. We can break up area A' into many tiny areas, where each
tiny area a is a distance y from the neutral axis. The average
normal stress acting on area A' at point 1 is the sum of the normal
stresses acting on all of the tiny areas, so
σ
1avg
=
∑
y
c
M
1
y
I
. The normal force acting on area A' at point 1 is the average
stress times the sum of these tiny areas, so
P
1
=
∑
y
c
M
1
y a
I
=
M
1
I
∑
y
c
y a
. Since
∑
y
c
y a=y A'
,
P
1
=
M
1
y A'
I
. Similarly,
the normal force acting on area A' at point 2 is
P
2
=
M
2
y A '
I
. The shear force
V
H
=P
2
−P
1
=
(M
2
−M
1
) y A '
I
.
The value of the bending moment at any point along a beam equals the area of the shear diagram up to that point, so
M
1
=V x
and
M
2
=V (x+Δ x)
. The difference of the two moments is
M
2
−M
1
=V (x+Δ x)−V x=V⋅Δ x
. Substitute
87
Loose cards
1 card on
glued deck
2 glued decks
P
P
P
P
A B
R
A
R
B
V
M
M
1
End view
y
area A'
shear plane
Free-body
diagram
of area A'
Δx
1 2
Δx
P
1
V
H
P
2
M
2
x
c
area A'
y
y
shear plane
area a
centroid of area A'

Chapter 9: Stresses in Beams
this result into the shear force equation, and we have
V
H
=
V Δ x y A'
I
.
The shear stress acting in the shear plane equals the shear force V
H
divided by the area it acts on: the thickness of the beam
in the shear plane times the length of beam between points 1 and 2:
τ=
V
H
t Δ x
=
V Δ x y A'
I t Δ x
=
V y A'
I t
. The product
y A'
is
the first moment of area A' about the neutral axis, defined as the variable
Q= y A'
. Substituting, we have the General
Shear Formula for beams:
τ=
V Q
I t
.
!%
Calculate the shear stress in a rectangular beam at five locations: at the neutral axis, ¼ of the way between the neutral axis
and the top of the beam, ½ way, ¾ of the way, and at the top of the beam.
% When the shear plane is at the neutral axis,
y=
h
4
and
A' =
bh
2
, so
Q= y A'=
h
4
bh
2
=
bh
2
8
. The moment of
inertia of a rectangle is
I =
bh
3
12
and the thickness of the beam at the shear plane is
t=b
. The shear stress is
τ=
VQ
I t
=
V bh
2
8
12
bh
3
b
=
3V
2bh
-
y=
5
16
h
and
A' =
3
8
bh
, so
Q= y A'=
5h
16
3bh
8
=
15bh
2
128
. The other two variables in the General Shear Equation,
I and t, are the same as before, so the shear stress is
τ=
VQ
I t
=
V 15 bh
2
128
12
bh
3
b
=
45 V
32 bh
.
y=
3
8
h
and
A' =
1
4
bh
, so
Q= y A'=
3 h
8
bh
4
=
3bh
2
32
and
τ=
VQ
I t
=
V 3 bh
2
32
12
bh
3
b
=
9V
8bh
2
y=
7
16
h
and
A' =
1
8
bh
, so
Q= y A'=
7 h
16
bh
8
=
7bh
2
128
and
τ=
VQ
I t
=
V 7 bh
2
128
12
bh
3
b
=
21V
32 bh
4
y=
1
2
h
and
A' =0
, so
Q= y A'=0
and
τ=
VQ
I t
=0
We can plot the results from this Example problem as a function of depth (red dots
at the right). The shear stress profile for a rectangular beam looks like a parabola.
The shear stress is a maximum at the neutral axis, diminishing to zero at the top and
bottom surfaces. The profile looks different for wide-flange beams because the area
is distributed differently, but the maximum shear stress will still be at the core and
the surface will have zero shear stress.
88
h
b
area A'
y
shear
plane
centroid of
area A'
area A'
y
h/4
area A'
y
h/8
area A'
y3h/8
area A' = 0
y
h/2
Case 1 Case 2
Case 3 Case 4 Case 5
Shear stress profile End view

Chapter 9: Stresses in Beams
!&
A round 1.5 cm diameter rod is loaded in bending with a point load of 300 N
at the midspan. Calculate the shear stress at the neutral axis. Report the result
in MPa.
The loading is symmetrical, so the reaction forces equal half the
applied load:
R
A
=R
B
=
300 N
2
=150 N
. Draw the shear diagram to find the
maximum shear load,
V
max
=R
A
=150 N
.
From Appendix C, the centroid of area A' is at
y=
2 d
3 π
.
Area A' is half the area of the circle:
A' =
1
2
π d
2
4
=
π d
2
8
.
Calculate
Q= y A'=
2 d
3 π
π d
2
8
=
d
3
12
. The moment of inertia of a circle is
I =
π d
4
64
, and the thickness of the beam at the
shear plane is d.
Combine terms to find shear stress,
τ=
VQ
I t
=
V d
3
12
64
π d
4
d
=
16V
3π d
2
=
16⋅150 N
3 π(1.5 cm)
2
∣
MPa m
2
10
6
N
∣
(100 cm)
2
m
2
=1.13 MPa
Another way to solve this problem is to calculate numerical answers for
y
, A', Q, and I, with appropriate unit conversions,
then calculate τ. Try it both ways, and you will find that the algebraic solution is shorter and requires fewer keystrokes on
the calculator, which means fewer opportunities for error.
The General Shear Formula works well for simple shapes where
y
and A' are easy to calculate. Steel
wide-flange beams have a more complicated shape, so we can approximate the shear stress at the neutral
axis using the Average Web Shear Approach:
τ=
V
d t
w
where d is the depth of the beam and t
w
is the
thickness of the web.
!'
A W4×13 steel wide-flange beam is loaded in bending with a point load of 6
kips at the midspan. Calculate the shear stress at the neutral axis. Report the
result in ksi.
The loading is symmetrical, so the reaction forces equal half the
applied load:
R
A
=R
B
=
6 kips
2
=3 kips
. From the shear diagram, the
maximum shear load
V
max
=R
A
=3 kips
. Use the Average Web Shear
Approach to find the shear stress at the neutral axis:
τ=
V
d t
w
=
3 kips
4.16in.×0.280 in.
=2.58 ksi
.
89
P = 6 kips
A B
3 kips
3 kips
V
3 kips
-3 kips
L/2 L/2
P = 300 N
A B
L/2 L/2
150 N 150 N
V
150 N
-150 N
shear
plane
area A'
y
d
t
w
Chapter 9: Stresses in Beams
How does the calculated shear stress compare with the actual shear strength of the material? While yield and ultimate
strengths are easy to find in reference books and on the internet, shear strengths are rarely reported. A good estimate for
steels is
τ
allowable
=0.4 σ
YS
. If the beam in the previous Example is made of A36 steel with a yield strength of 36 ksi, the
allowable shear stress is
τ
allowable
=0.4 (36 ksi)=14.4 ksi>τ
applied
, therefore the beam will not fail in shear.
In most of the problems so far, we have assumed that the beams are weightless. Real beams have real weight, so we need to
include the weight as a uniform distributed load along the length of the beam.
90

Chapter 9: Stresses in Beams
!(
A 36 foot long W12×30 steel wide-flange
beam is loaded in bending with a point
load of 5 kips located 24 feet from the left
end. The beam also has weight. Calculate
the allowable bending moment in the
beam. Calculate the maximum bending
stress and maximum shear stress, and
report the result in ksi. Report the
locations of these maximum points.
The loading is not symmetrical,
so use an equivalent load diagram, sum of
the moments and sum of the forces to find
the reaction forces. A W12×30 beam has
a weight per unit length
w=30 lb./ft.
, so
the equivalent point load
W =
30lb.
ft.
36ft.
∣
kip
10
3
lb.
=1.08 kips
at the midspan.
The moment about point A is
∑
M
A
=0=−1.08 kips⋅18ft.−5 kips⋅24ft.+R
B
⋅36ft.
Rewrite the equation to find the reaction force
R
B
=
1.08 kips⋅18ft.+5kips⋅24ft.
36 ft.
=3.873 kips
Sum of the forces
∑
F
y
=0=R
A
−1.08 kips−5 kips+3.873 kips
. Solve for the reaction force
R
A
=1.08kips+5 kips−3.873 kips=2.207 kips
. Calculate the inflection points on the shear diagram.
V
1
=R
A
=2.207 kips
,
V
2
=V
1
−
0.030 kips
ft.
24 ft.
=1.487 kips
,
V
3
=V
2
−5 kips=−3.5133 kips
,
V
4
=V
3
−
0.030 kips
ft.
12 ft.
=−3.873 kips
,
V
5
=V
4
+R
B
=0 kips
The maximum moment is the area of the left-hand trapezoid in the shear diagram:
M
max
=
2.207 kips+1.487 kips
2
24ft.
=44.3 kip⋅ft.
The allowable bending moment
M
allowable
=0.6 σ
YS
Z =
0.6⋅50 kips⋅43.1 in.
3
in.
2
∣
ft.
12 in.
=107.8 kip⋅ft.
Since
M
allowable
>M
applied
, the beam is strong enough to support the existing loads in bending.
The maximum bending stress in the beam is
σ=
M
Z
=
44.3 kip⋅ft.
43.1 in.
3
∣
12in.
ft.
=12.34 ksi
, and it occurs at the point load.
From the shear diagram, the maximum shear load
∣
V
max
∣
=3.873 kips
. Use the Average Web Shear Approach to find the
maximum shear stress
τ=
V
d t
w
=
3.873 kips
12.34 in.×0.260 in.
=1.21ksi
, which occurs at point B.
91
w
beam
= 30 lb./ft.
= 0.030 kips/ft.
R
B
R
A
A B
24 ft.
12 ft.
V
1
=2.207 kips
V
V
4
= -3.873 kips
V
5
= 0 kips
P = 5 kips
V
3
= -3.513 kips
M
M
max
= 44.3 kip∙ft.
=
R
B
R
A
A B
Equivalent load diagram
18 ft.
W = 1.08 kips
24 ft.
P = 5 kips
V
2
= 1.487 kips

Chapter 9: Stresses in Beams
*#"
Design engineers select beams that will support known loads. However, in
many cases the structure already exists, and will be used with a different
loading condition than it was originally intended. A manufacturing plant may
bring in a larger piece of equipment, so the engineer calculates whether the
existing floor will support the machine.
A simply-supported timber beam carries a uniform distributed load; how large
a load can the beam support? Since the loading is symmetrical, the reaction
forces equal half the applied load:
R
A
=R
B
=
w L
2
. The maximum shear load is
V
1
=R
A
=
w L
2
. The maximum moment equals the area of the left-hand triangle
in the shear diagram, or one half the base times the height:
M
max
=
1
2
L
2
w L
2
=
w L
2
8
. If we look at bending stress, then
σ=
M
S
=
w L
2
8 S
.
Rewrite the equation to solve for the load,
w=
8σ
allowable
S
L
2
. If we look at shear stress,
τ=
V Q
I t
=
w L Q
2 I t
. Rewrite the
equation to solve for the load,
w=
2 τ
allowable
I t
L Q
.
92
A B
wL/2 wL/2
V
1
=wL/2
V
V
3
= 0
V
2
= –wL/2
w
L
M
max
= wL
2
/8
M

Chapter 9: Stresses in Beams
!)
A simply-supported, 8 foot long, 4×8 southern yellow pine timber supports a
uniform distributed load. Calculate the maximum load the beam can support.
Report the result in lb./ft.
From the previous discussion, based on bending stress the beam can
support a total load of
w
total
=
8σ
allowable
S
L
2
. From the Appendix, the
allowable bending stress of southern yellow pine is 1400 psi and the section
modulus
S
x
=30.7in.
3
.
The total load is
w
total
=
8
(8 ft.)
2
1400lb.
in.
2
30.7in.
3
∣
ft.
12 in.
=448lb./ft.
. The
total load includes the beam's weight per unit length:
w
total
=w
applied
+w
beam
.
From the Appendix, a 4×8 timber has a weight of 7.05 lb./ft., so
w
applied
=w
total
−w
beam
=448 lb. /ft.−7.05lb./ft.=441 lb./ft.
Also from the previous discussion, based on shear stress the beam can
support a total load of
w
total
=
2 τ
allowable
I t
L Q
. From the Appendix,
I
x
=111in.
4
and
τ
allowable
=175 psi
.
Based on the dimensions,
y=
7.25 in.
4
=1.8125 in.
,
t=3.5in.
, and
A' =
3.5 in.⋅7.25 in.
2
=12.6875 in.
2
, so
Q=A' y=12.6875 in.
2
⋅1.8125in.=22.9961 in.
3
.
The total load is
w
total
=
2 τ
allowable
I t
L Q
=
2
8ft.
175lb.
in.
2
111 in.
4
22.9961 in.
3
3.5in.
=739lb. /ft.
.
The applied load is
w
applied
=739 lb./ft.−7.05lb./ft.=732 lb./ft.
The beam can support an applied load of 441 lb./ft. before
it fails in bending, and a load of 732 lb./ft. before it fails in shear. Pick the lower of the two numbers because this is where
failure will occur first.
+,
Use the Flexure Formula to find the bending stress in any beam other than a steel W-beam:
σ=
Mc
I
x
or
σ=
M
S
x
The allowable moment of a beam is
M
allowable
=
σ
allowable
I
x
c
or
M
allowable
=σ
allowable
S
x
For wide-flange steel beams only, the allowable moment is
M
allowable
=0.6 σ
YS
Z
x
and the bending stress is
σ=
M
Z
x
Use the General Shear Formula to find the maximum shear stress in a beam:
τ=
V Q
I t
where
Q= y A'
Use the Average Web Shear Approach to find the maximum shear stress in a wide-flange steel beam:
τ=
V
d t
w
For steels, use
τ
allowable
=0.4 σ
YS
93
A B
wL/2 wL/2
V
1
=wL/2
V
V
3
= 0
V
2
= –wL/2
w
8 ft.
M
max
= wL
2
/8
M
7.25 in.
3.5 in.
area A'
y
shear
plane
centroid of
area A'

Chapter 10: Beam Deflection
%?& C
0
A weightless beam with no loads has
a horizontal elastic curve. Pick two
points C and D that are a small
distance x apart. If we add a load, the
beam deflects, and the elastic curve
bows downward. Points C and D now
lie on an arc with a radius of
curvature, labeled R on the diagram.
At the bottom of the beam, points C
and D are now
x+δ
apart, because
the bottom of the beam has stretched
a little. Draw a vertical line through
point D, and we have a little triangle
with height c and base δ. We can use
the principle of similar triangles to
compare the little triangle with the
big triangle having a height R and
base x:
δ
c
=
x
R
. Rewrite the equation
to solve for
δ
x
=
c
R
. Along the
bottom surface of the beam, the strain is
ε=
δ
x
, so
ε=
c
R
. As long as the beam is elastic,
E=
σ
ε
, which we can rewrite as
ε=
σ
E
. Set the strain equations equal to each other, and
σ
E
=
c
R
. Solving for stress,
σ=
E c
R
. We know another equation
for bending stress in a beam:
σ=
M c
I
. Set the stress equations equal to each other, and
E c
R
=
M c
I
→
E
R
=
M
I
. Now
solve for radius of curvature,
R=
E I
M
.
This equation helps us calculate the radius of curvature at a given point along the length of a beam. There are some special
cases where the moment M is constant over a long length, so the elastic curve is a circular arc along this length.
!"
A 2 m long titanium beam is made of 1 cm square barstock. Two 50 N point
loads lie 0.25 meters from each end. What is the radius of curvature of the
beam between the two point loads? Report the answer in meters.
Draw the elastic curve, shear diagram, and moment diagram. The
loading is symmetrical, so the reaction forces
R
A
=R
B
=50 N
. The value of
the moment diagram between the point loads equals the area of the left-hand
rectangle in the shear diagram:
M =0.25 m⋅50 N=12.5 N⋅m
.
The moment of inertia of a square
I =
b h
3
12
=
b
4
12
.
The radius of curvature of the beam between the two point loads is
R=
E I
M
=
E b
4
12 M
=
114 GPa (1 cm)
4
12⋅12.5 N⋅m
∣
10
9
N
GPa m
2
∣
m
4
(100cm)
4
=7.6 m
94
A B
R
A
R
B
C
P
A BD
Elastic
curve
C
D
R
c
δ
x+δ
A B
R
A
R
B
C
A BD
Elastic
curve
C
D
c
x
Beam with no load
Loaded beam
R
x
c
δ
x
Elastic
curve
A B
50 N 50 N
V
M
max
= 12.5 N∙m
0.25 m
50 N
0.25 m
1.5 m
M
V
1
= 50 N
50 N
V
2
= 0
V
3
= –50 N
V
4
= 0

Chapter 10: Beam Deflection
The blade on a bandsaw obeys the radius of curvature equation because the blade flexes elastically, and forms a
semicircular arc at each bandsaw wheel.
In a few rare cases, we can calculate the maximum deflection of a beam using the radius of curvature, as in the following
example.
!#
A 2 m long titanium beam is made of 1 cm square
barstock. Two 50 N point loads lie at the ends, and
the supports lie 0.25 meters from each end. What
is the maximum deflection at the midspan? Report
the answer in cm.
This problem is like Example #1 but
flipped upside down. Draw the elastic curve with
its radius of curvature and the center of curvature
(cross at the bottom of the figure). The distance
from the center of curvature to the beam is R; the
beam deflects a distance Δ
max
at the midspan; and
the distance from the center of curvature to the
undeflected beam is
R−Δ
max
. The base of the
shaded triangle is half the distance between the
supports, 0.75 m. Use the Pythagorean Theorem to
find the height of the triangle,
R−Δ
max
=
√
R
2
−(0.75 m)
2
=
√
(7.6 m)
2
−(0.75 m)
2
=7.563 m
Deflection at the midspan
Δ
max
=R−(R−Δ
max
)=
7.600 m−7.563 m
∣
100 cm
m
=3.71 cm
+'
We can use the Radius of Curvature Method to calculate deflection as long as the moment is constant. From the examples in
previous chapters, we know that the moment usually changes along the length of a beam. There are a number of geometrical
and calculus-based techniques for calculating deflection in these cases. Engineers have compiled these solutions in
handbooks, so future engineers can use a worked-out algebraic solution, instead of deriving the solution from scratch. The
most useful compilation is Roark's Formulas for Stress and Strain, which contains many hundreds of formulas for beams,
shells, membranes, pressure vessels, and columns.
Look in the Appendix for Formula Method solutions for various beam problems. Each case includes a load diagram, shear
diagram, moment diagram, reaction forces and moments, and formulas for shear, moment, the slope at the ends, and
deflection at various positions along the beam. Use the Appendix to find values for E and I, then solve.
95
Elastic
curve
A B
50 N
50 N
V
M= –12.5 N∙m
0.25 m
50 N
0.25 m1.5 m
M
V
1
= –50 N
50 N
V
2
= 0
V
3
= 50 N
V
4
= 0
R
R
R–Δ
max
0.75 m
Δ
max

Chapter 10: Beam Deflection
!$
Use the Formula Method to calculate the maximum deflection of a simply-
supported 8-foot 4×4 Southern yellow pine timber loaded with a 200 lb.
point load at the midspan. Report the result in inches.
From Appendix F, the deflection at the midspan
Δ
max
=
P L
3
48 E I
,
where Young's modulus is 1700 ksi and the moment of inertia is 12.5 in.
4
.
Δ
max
=
200lb.(8 ft.)
3
48 ⋅12.5in.
4
in.
2
1700 kip
∣
(12 in.)
3
ft.
3
∣
kip
10
3
lb.
=0.17in.
!%
Use the Formula Method to calculate the maximum deflection of a
cantilever 8-foot 4×4 Southern yellow pine timber loaded with a 200 lb.
point load at the end. Report the result in inches.
Calculate the slope at the end of the beam; report the result in degrees.
From the Appendix, the deflection at the free end
Δ
max
=
P L
3
3E I
.
The moment of inertia and Young's modulus are the same as in the
previous Example.
Δ
max
=
200lb.(8 ft.)
3
3⋅12.5 in.
4
in.
2
1700 kip
∣
(12 in.)
3
ft.
3
∣
kip
10
3
lb.
=2.78in.
The equation for the slope at the free end is in radians, so include a conversion factor for degrees:
θ=
P L
2
2 E I
=
200lb. (8 ft.)
2
2 ⋅12.5 in.
4
in.
2
1700 kip
∣
(12 in.)
2
ft.
2
∣
kip
10
3
lb.
∣
180°
rad
=7.81°
When the point load on a cantilever beam is at the end of the beam, the elastic curve is an arc. If the point load is located
away from the end, then the elastic curve is an arc from the wall to the point load, and a straight line between the point load
and the end of the beam. This portion of the beam is sloped but straight.
96
P = 200 lb.
A B
4 ft. 4 ft.
100 lb.
100 lb.
Elastic
curve
Δ
max
1600 ft.⋅lb.
P = 200 lb.
A B
8 ft.
200 lb.
Elastic
curve
Δ
max
θ

Chapter 10: Beam Deflection
!&
A cantilever 8-foot 4×4 Southern yellow pine timber loaded with a 200 lb.
point load 2 feet from the end. Use the Formula Method to calculate the
deflection at the point load. Calculate the deflection at the point load and
the maximum deflection at the end. Report the results in inches.
From Appendix F, the deflection at point C is
Δ
C
=
P b
3
3 E I
, where
b is the distance from the point load to the wall. The moment of inertia and
Young's modulus are the same as in the previous two Examples.
Δ
C
=
200 lb.(6ft.)
3
3⋅12.5in.
4
in.
2
1700kip
∣
(12 in.)
3
ft.
3
kip
10
3
lb.
=1.17 in.
The slope of the straight portion of the beam from point C to the left end is
θ=
P b
2
2 E I
=
200lb. (6 ft.)
2
2⋅12.5in.
4
in.
2
1700 kip
∣
(12 in.)
2
ft.
2
∣
kip
10
3
lb.
∣
180°
rad
=4.39°
.
The portion of the beam to the left of the point load is a straight line. Use
trigonometry to find the maximum deflection:
tan θ=
y
2ft.
so
y=
2ft. tan (4.39° )
∣
12in.
ft.
=1.84 in.
and
Δ
max
=y +Δ
C
=1.84 in.+1.1 in.=3.01 in.
97
1200 ft.⋅lb.
P = 200 lb.
A B
6 ft.
200 lb.
2 ft.
Elastic
curve
Δ
max
θ
arc
line
Δ
C
C
Δ
max
Δ
C
θ
y
line
2 ft.

Chapter 10: Beam Deflection
+':
Some Formula Method equations have
conditions. Consider a simply-supported beam
with a single point load located at a distance a
from the left end. The deflection at a distance x
from the left end is
Δ
x
=
P b x
6 E I L
(L
2
−b
2
−x
2
)
when
x< a
, so this equation is restricted to
the portion of the beam to the left of the point
load. What if we want the deflection at a
location to the right of the point load? Redraw
the beam as a left-to-right mirror image,
swapping dimensions a and b, and solve for
the deflection.
!'
A simply-supported 36 cm long steel beam
is loaded with a 6.5 kN point load 8 cm
from the left end. The beam is made of 1.2
cm square barstock. Use the Formula
Method to calculate the deflection 24 cm
from the left end. Report the results in mm.
From Appendix F, the
deflection at a distance x from the left end
is
Δ
x
=
P b x
6 E I L
(L
2
−b
2
−x
2
)
when
x< a
.
Since
x> a
, we have to draw a mirror image of the loading case.
The moment of inertia is
I =
bh
3
12
=
b
4
12
=
(1.2 cm)
4
12
=0.1728 cm
4
Δ
x
=
6.5 kN⋅8cm⋅12 cm
6⋅207GPa ⋅0.1728 cm
4
⋅36 cm
∣
GPa m
2
10
6
kN
∣
(100cm )
2
m
2
×
(
(36 cm)
2
−(8 cm)
2
−(12 cm)
2
)
∣
10 mm
cm
=8.79mm
+'1&
The Formula Method equations in the Appendix
apply to simple loading cases. Many loading
conditions are more complex, but you can
separate a complex loading condition into its
parts, solve for V, M, or Δ at any location along
the beam, then add the results together to find the
total V, M, or Δ at that location:
Δ
total
=Δ
1
+Δ
2
+Δ
3
+...Δ
n
for n cases.
98
P
A B
a b
R
A
R
B
L
Elastic
curve
Δ
x
x
P
B A
a b
R
B
R
A
L
Elastic
curve
Δ
x
x
Original Mirror image
6.5 kN
A B
8 cm
28 cm
R
A
R
B
36 cm
Elastic
curve
Δ
x = 24 cm
24 cm
6.5 kN
B A
R
B
R
A
36 cm
Elastic
curve
Δ
x = 12 cm
Original
Mirror image
12 cm
28 cm
8 cm
P
A B
w
=
P
A B
+
A B
w
x
x x
C C C

Chapter 10: Beam Deflection
!(
A simply-supported 200 cm long, 51 mm
standard steel pipe is loaded with a uniform
distributed load of 400 N/m and a point load
of 8 kN located 25 cm from the right end.
Use the Formula Method and Superposition
to calculate the deflection at the midspan (at
x=1 m
). Report the results in mm.
From Appendix F, the deflection due to the point load at a distance x from the left end is
Δ
1
=
P b x
6 E I L
(L
2
−b
2
−x
2
)
. At the midspan,
x=
L
2
, so
Δ
1
=
P b L
6 E I L 2
(
L
2
−b
2
−
(
L
2
)
2
)
=
P b
12 E I
(
3
4
L
2
−b
2
)
. In this
equation, b is 25 cm. Also from the Appendix, a 51 mm standard steel pipe has a moment of inertia
I =0.276×10
6
mm
4
Δ
1
=
8kN ⋅25 cm
12 ⋅207GPa ⋅0.276×10
6
mm
4
∣
GPa m
2
10
6
kN
∣
(10
3
mm)
2
m
2
∣
10 mm
cm
×
(
0.75(200 cm)
2
−(25 cm)
2
)
∣
(10 mm)
2
cm
2
=8.57 mm
The deflection due to the distributed load at the midspan is
Δ
2
=
5w L
4
384 E I
Δ
2
=
5
384
400 N
m
(200 cm)
4
207GPa ⋅0.276×10
6
mm
4
∣
GPa m
2
10
9
N
∣
10
3
mm
m
∣
(10 mm)
4
cm
4
=1.46 mm
Δ
total
=Δ
1
+Δ
2
=8.57 mm+1.46 mm=10.03 mm
In the previous Example, the maximum deflection due to the uniform distributed load is at the midspan (x = 1 m), but the
maximum deflection due to the point load is located at
x=
√
a (a +2b)
3
=
√
175 cm(175 cm+2(25 cm))
3
=114.5 cm
, to the
right of the midspan. Using the Method of Superposition, you can add the shear, moment, or deflection at a given point
along the beam, but you cannot add the maximum shear, moment, or deflection, unless they occur at the same point along
the beam. One example is a simply-supported beam with a point load at the midspan and a uniform distributed load; both
loading conditions have the maximum deflection and maximum moment at the midspan.
Example #7 does not consider the weight of the pipe. From Appendix D, the mass per unit length is 5.44 kg/m. The SI unit
of weight is the newton, equal to a kilogram meter per second squared. Multiply mass by gravity to get weight.
W
L
=
m g
L
=
5.44kg
m
9.81m
s
2
∣
N s
2
kg m
=53.4 N/m
99
P = 8 kN
A B
w = 400 N/m
=
A B
+
A B
25 cm
200 cm
8 kN 400 N/m

Chapter 10: Beam Deflection
38 C
We can use the Formula Method for calculating the deflection of a beam at many points along its length, then graphing the
result to see the deflection curve.
!)
A 150×360 Douglas fir timber is loaded as shown. Use the Formula Method to
calculate the deflection at 1 meter increments from left to right. Graph the
deflection vs. position along the beam. Ignore the weight of the beam.
From Appendix D,
E =11.7 GPa
and
I =471×10
6
mm
4
.
Since point A is pinned,
Δ
0ft.
=0
.
From Appendix F, the deflection equation for this loading condition is .
Δ
x
=
P b x
6 E I L
[
L
2
−b
2
− x
2
]
for
x<a
where
a=2m
and
b=8 m
. We can use this equation for
x=1m
.
At
x=1m
,
Δ
1 m
=
3 kN (8 m)(1 m)
[
(10 m)
2
−(8 m)
2
−(1 m)
2
]
6 11.7 GPa 471×10
6
mm
4
10 m
∣
GPa m
2
10
6
kN
∣
(10
3
mm)
5
m
5
=2.54mm
At
x=2 m
(the point load), it is easier to use
Δ
2 m
=
P a
2
b
2
3 E I L
Δ
2 m
=
3 kN (2 m)
2
(8 m)
2
3 11.7 GPa 471×10
6
mm
4
10 m
∣
GPa m
2
10
6
kN
∣
(10
3
mm)
5
m
5
=4.65 mm
To the right of the point load,
x>a
, so we need to flip the diagram. Let's call the new
dimensions a' and b':
a' =8 m
and
b' =2 m
. We also need new values of x, starting
at point B and moving right in the mirror image...let's call it x'.
The value of x' is calculated as
x' =L− x
, so
Δ
x
=
P b' x '
6 E I L
[
L
2
−b'
2
−x '
2
]
At
x=3m, x '=7 m
,
Δ
3 m
=
3 kN (2 m)(7 m)
[
(10 m)
2
−(2 m)
2
−(7 m)
2
]
6 11.7GPa 471×10
6
mm
4
10 m
∣
GPa m
2
10
6
kN
∣
(10
3
mm)
5
m
5
=5.97 mm
At
x=4 m, x ' =6 m
,
Δ
4 m
=
3 kN (2 m)(6 m)
[
(10 m)
2
−(2 m)
2
−(6 m)
2
]
6 11.7 GPa 471×10
6
mm
4
10 m
∣
GPa m
2
10
6
kN
∣
(10
3
mm)
5
m
5
=6.53mm
At
x=5m, x '=5m
,
Δ
5 m
=
3 kN (2 m)(5 m)
[
(10 m)
2
−(2 m)
2
−(5 m)
2
]
6 11.7 GPa 471×10
6
mm
4
10 m
∣
GPa m
2
10
6
kN
∣
(10
3
mm)
5
m
5
=6.44 mm
At
x=6 m, x ' =4 m
,
Δ
6 m
=
3 kN (2 m)(4 m)
[
(10 m)
2
−(2 m)
2
−(4 m)
2
]
6 11.7 GPa 471×10
6
mm
4
10 m
∣
GPa m
2
10
6
kN
∣
(10
3
mm)
5
m
5
=5.81 mm
At
x=7 m, x ' =3 m
,
Δ
7 m
=
3 kN (2 m)(3 m)
[
(10 m)
2
−(2 m)
2
−(3 m)
2
]
6 11.7GPa 471×10
6
mm
4
10 m
∣
GPa m
2
10
6
kN
∣
(10
3
mm)
5
m
5
=4.74 mm
100
3 kN
R
B
R
A
A B
2 m
8 m
a b
x
3 kN
R
A
R
B
B A
2 m
8 m
a'
b'
x'
Mirror Image

Chapter 10: Beam Deflection
!)
At
x=8m, x '=2 m
,
Δ
8 m
=
3 kN(2 m)(2 m)
[
(10 m)
2
−(2 m)
2
−(2 m)
2
]
6 11.7GPa 471×10
6
mm
4
10 m
∣
GPa m
2
10
6
kN
∣
(10
3
mm)
5
m
5
=3.34 mm
At
x=9m, x' =1 m
,
Δ
9 m
=
3 kN (2 m)(1 m)
[
(10 m)
2
−(2 m)
2
−(1 m)
2
]
6 11.7 GPa 471×10
6
mm
4
10 m
∣
GPa m
2
10
6
kN
∣
(10
3
mm)
5
m
5
=1.72mm
Since point B is pinned,
Δ
10ft.
=0
Deflection is plotted as negative numbers to show the beam deflecting downward under the applied load. Although the
point load is 2 meters from the left end, the maximum deflection is at 4 meters.
+,
If a beam segment has a constant moment, then the radius of curvature of that segment of beam is
R=
E I
M
. The bending
stress in this segment of the beam is
σ=
E c
R
.
101
0 1 2 3 4 5 6 7 8 9 10
-7
-6
-5
-4
-3
-2
-1
0
Distance along the beam (m)
Deflection
(mm)

Chapter 11: Beam Design
%%&
(,+ 1
In the previous three chapters, we learned how to calculate reaction forces and moments, how to draw shear and moment
diagrams, how to calculate deflection, and how to calculate bending and shear stresses for a given beam size and shape.
When you design a beam, you start with the applied loads, beam length, allowable stresses (and sometimes allowable
deflection), and you must figure out what size beam to use. Use these six steps, and you can design a wide-flange steel
beam.
% Identify all applied loads and design constraints (beam length, yield strength, and maximum deflection if specified).
- Draw the load diagram and calculate the reactions. Draw an equivalent load diagram if necessary.
. Draw shear and moment diagrams, and calculate V
max
and M
max
.
2 Select the lightest beam from Appendix D that will support M
max
, or has enough stiffness to limit Δ
max
. The allowable
moment in a steel beam
M
allowable
=0.6 σ
YS
Z
x
, so the required plastic section modulus is
Z
required
=
M
0.6 σ
YS
=
1.67 M
σ
YS
. Solve
for Z
required
, then find the lightest W-beam that has a slightly larger value of Z.
U.S. Customary beams are identified by nominal depth and weight per unit length. For example, W12×40 is about 12 in.
deep, and weighs 40 lb./ft.
Metric beams are identified by nominal depth and mass per unit length. For example, W360×110 is about 360 mm deep, and
has a mass of 110 kg/m; convert to weight per unit length by multiplying by gravity (9.81 m/s
2
), using the definition of a
newton,
N =
kg⋅m
s
2
, to convert units:
w=
m
L
g=
110 kg
m
9.81 m
s
2
∣
N s
2
kg m
∣
kN
10
3
N
=1.08 kN/m
If the maximum deflection is specified, write the equation for Δ
max
, solve it for I
required
, then find the lightest W-beam that has
a slightly larger value of I.
4 Add the beam weight to the load diagram, and recheck moment and deflection. You may have to draw completely
new shear and moment diagrams. If
Z
beam
>Z
required
, the beam is OK in bending, and if
I
beam
>I
required
, the beam is OK in
deflection. If either of these conditions is not met, pick a larger beam and recalculate.
9 Check shear. For steel W-beams,
V
applied
≤0.4 σ
YS
d t
w
where d is the beam depth and t
w
is the thickness of the web.
As long as this inequality is true, the beam is OK in shear.
The rule of thumb in these calculations is to use a beam that has
more than you need (more I, more Z, more shear strength). Just
like in real life, having more than you need is usually better than
having less than you need (money, food, education, happiness,
etc.)
102
Web thickness, t
w
x
Beam depth, d
Flange thickness, t
f
Flange width, b
f
x
y
y
flange
web

Chapter 11: Beam Design
!"
Select the lightest W-beam that will support a uniform distributed
load of 3 kip/ft. on a span of 20 ft.
% Identify loads and design constraints:
w=3 kip/ft.
L=20ft.
σ
YS
=50 ksi
Δ
max
is not constrained
- The loading is symmetrical:
R
A
=R
B
=
w L
2
=
3 kips
ft.
20 ft.
2
=30 kips
.
V
max
=30 kips
;
M
max
=
w L
2
8
=
3kips
ft.
(20 ft.)
2
8
=150 kip⋅ft.
2
Z
required
=
1.67 M
σ
YS
=
1.67⋅150 kip⋅ft. in.
2
50 kips
∣
12 in.
ft.
=60.1in.
3
Look in Appendix D for the lightest W-beam for which
Z >Z
required
. W18×35 has a plastic section modulus of 66.5 in.
3
and
is 35 lb./ft.; all other beams that meet the Z constraint are heavier.
4 Add the beam weight to the shear and moment diagrams,
and recalculate the maximum values. Since the shape of these
diagrams has not changed, we can use the same equations as
before, adding the beam weight to the applied weight.
R
A
=R
B
=V
max
=
(w
applied
+w
beam
)L
2
=
3.035 kips
ft.
20 ft.
2
=30.35 kips
M
max
=
(w
applied
+w
beam
)L
2
8
=
3.035 kips
ft.
(20ft.)
2
8
=151.8 kip⋅ft.
Z
required
=
1.67 M
σ
YS
=
1.67⋅151.8 kip⋅ft. in.
2
50 kips
∣
12 in.
ft.
=60.8in.
3
We have
Z
beam
=66.5in.
3
Since
Z
beam
>Z
required
, the beam is OK in bending.
9 The beam will support a shear load of
0.4 σ
YS
d t
w
=0.4⋅50
kips
in.
2
⋅17.7in.⋅0.300 in.=106 kips
Since we are
applying only 30.35 kips in shear, the beam is OK in shear.
Real engineering problems have multiple constraints. In the previous problem, we designed a beam that was strong enough
to support the applied load and its own weight, without failing in bending or shear. In the next problem, we will add another
constraint: maximum deflection. In many structures, deflection governs design; for example, most people feel
uncomfortable walking across a strong floor that moves too much.
103
A B
R
A
= 30 kips
V
1
=30 kips
V
V
3
= 0
V
2
= -30 kips
20 ft.
M
max
= 150 ft.∙kips
M
R
B
= 30 kips
w
applied
= 3 kips/ft.
A B
30.35 kips
V
1
=30.35 kips
V
V
3
= 0
V
2
= -30.35 kips
20 ft.
M
max
= 151.8 ft.∙kips
M
30.35 kips
w
beam
= 0.035 kips/ft.
w
applied
Applied load + beam weight
Applied load only

Chapter 11: Beam Design
!#
Select the lightest W-beam that will support a uniform distributed
load of 3 kip/ft. on a span of 20 ft., and deflects no more than 0.6 in.
% Identify loads and design constraints:
w=3 kip/ft.
L=20 ft.
σ
YS
=50 ksi
Δ
max
=0.6 in.
-D. These steps are identical to Example #1:
R
A
=R
B
=30 kips
,
V
max
=30 kips
, and
M
max
=150 kip⋅ft.
2
Z
required
=60.1in.
3
as in Example #1, therefore we should try
W18×35 which has a plastic section modulus of 66.5 in.
3
For this loading case,
Δ
max
=
5 w L
4
384 E I
. The moment of inertia
required to support the deflection constraint is
I
required
=
5 w L
4
384 E Δ
max
=
5
384
3 kips
ft.
(20ft.)
4
in.
2
30×10
3
kip
0.6 in.
∣
(12 in.)
3
ft.
3
=600 in.
4
.
The moment of inertia of a W15×35 beam is 510 in.
4
... not enough.
The lightest W-beam with
I >600in.
4
is W21×50, which has
I
x
=984 in.
4
and
Z
x
=110 in.
3
4 Add beam weight to shear and moment diagrams; recalculate
the max. values. The shape of the diagrams is unchanged; use the
same equations as before, adding beam weight to applied weight.
R
A
=R
B
=V
max
=
(w
applied
+w
beam
) L
2
=
3.05 kips
ft.
20 ft.
2
=30.5 kips
M
max
=
(w
applied
+w
beam
) L
2
8
=
3.05kips
ft.
(20 ft.)
2
8
=152.5 kip⋅ft.
Z
required
=
1.67 M
σ
YS
=
1.67⋅152.5 kip⋅ft. in.
2
50 kips
∣
12 in.
ft.
=61.1 in.
3
We have
Z
beam
=110in.
3
Since
Z
beam
>Z
required
, the beam is OK in
bending.
I
required
=
5(w
applied
+w
beam
)L
4
384 E Δ
max
=
5
384
3.05 kips
ft.
(20 ft.)
4
in.
2
30×10
3
kip
0.6in.
∣
(12 in.)
3
ft.
3
=610in.
4
We have
I
beam
=984 in.
4
. Since
I
beam
>I
required
, the beam is OK in deflection.
9 The beam will support a shear load of
0.4 σ
YS
d t
w
=0.4⋅50
kips
in.
2
⋅20.8 in.⋅0.380 in.=158 kips
Since we are
applying only 30.5 kips in shear, the beam is OK in shear.
In these two Examples, the shear and moment diagrams retained their shapes when we added the weight of the beam. In
most loading cases, we need to draw new shear and moment diagrams, as in Example #3.
104
A B
R
A
= 30 kips
V
1
=30 kips
V
V
3
= 0
V
2
= -30 kips
20 ft.
M
max
= 150 ft.∙kips
M
R
B
= 30 kips
w
applied
= 3 kips/ft.
Applied load only
A B
30.5 kips
V
1
=30.5 kips
V
V
3
= 0
V
2
= -30.5 kips
20 ft.
M
max
= 152.5 ft.∙kips
M
30.5 kips
w
beam
= 0.050 kips/ft.
w
applied
Applied load + beam weight

Chapter 11: Beam Design
!$
Select the lightest W-beam that will support a point load of 6 kips
located 4 feet from the left end of a 12 ft. span.
% Identify loads and design constraints:
P =6 kips
L=12 ft.
σ
YS
=50 ksi
Δ
max
is not constrained
- For this loading case,
R
A
=
P b
L
=
6 kips⋅8 ft.
12 ft.
=4 kips
and
R
B
=
P a
L
=
6 kips ⋅4 ft.
12 ft.
=2 kips
. From the shear and moment diagrams,
V
max
=4 kips
and
M
max
=4 kips⋅4ft.=16 kip⋅ft.
2
Z
required
=
1.67 M
σ
YS
=
1.67⋅16 kip⋅ft. in.
2
50 kips
∣
12 in.
ft.
=6.41 in.
3
From Appendix D, the best choice is W8×10 which has a
Z
x
=8.87in.
3
and a weight per unit length of 10 lb./ft.
4 Add beam weight to the load diagram; redraw shear &
moment diagrams. Use the Method of Superposition to add the
effects of the point load and the beam weight to find the reactions.
R
A
=
P b
L
+
w
beam
L
2
=
6 kips ⋅8 ft.
12ft.
+
0.010 kips
ft.
12 ft.
2
=4.06 kips
R
B
=
P a
L
+
w
beam
L
2
=
6 kips ⋅4 ft.
12 ft.
+
0.010 kips
ft.
12 ft.
2
=2.06 kips
V
1
=R
A
=4.06 kips
V
2
=V
1
−w
beam
4ft.=4.02 kips
V
3
=V
2
−6kips=−1.98 kips
V
4
=V
3
−w
beam
8ft.=−2.06 kips
V
5
=V
4
+R
B
=0 kips
Since the maximum moment for the point
load occurs at the point load, and the maximum moment for the beam weight occurs at the midspan, we cannot add the
M
max
equations for each case. Instead, use the area of the first trapezoid in the shear diagram to find
M
max
=
(
4.06 kips+4.02 kips
2
)
⋅4ft.=16.16 kip⋅ft.
Z
required
=
1.67 M
σ
YS
=
1.67⋅16.16 kip⋅ft. in.
2
50 kips
∣
12 in.
ft.
=6.48 in.
3
We
have
Z
beam
=8.87in.
3
Since
Z
beam
>Z
required
, the beam is OK in bending.
9 The beam will support a shear load of
0.4 σ
YS
d t
w
=0.4⋅50
kips
in.
2
⋅7.89 in.⋅0.17in.=26.8 kips
Since we are
applying only 4.06 kips in shear, the beam is OK in shear.
105
A B
R
A
= 4 kips
V
1
=4 kips
V
V
3
= 0
V
2
= -2 kips
L = 12 ft.
M
max
= 16 ft.∙kips
M
R
B
= 2 kips
P = 6 kips
Applied load only
a = 4 ft. b = 8 ft.
A B
4.06 kips
V
1
=4.06 kips
V V
5
= 0
V
4
= -2.06 kips
L = 12 ft.
M
max
= 16.16 ft.∙kips
M
2.06 kips
P = 6 kips
Applied load + beam weight
a = 4 ft. b = 8 ft.
w
beam
= 0.010 kips/ft.
V
2
=4.02 kips
V
3
=-1.98 kips

Chapter 11: Beam Design
!%
Select the lightest W-beam that will support the point loads shown.
% Identify loads and design constraints.
σ
YS
=345 MPa
Δ
max
is not constrained
- Use Sum of the Moments and Sum of the Forces to find the
reaction forces.
R
B
=
−40 kN ⋅1 m+180 kN ⋅3m
5 m
=100 kN
R
A
=40 kN+180 kN−100 kN=120 kN
. Calculate the values for shear and moment diagrams.
V
1
=−40 kN
,
V
2
=V
1
+R
A
=80 kN
V
3
=V
2
−180 kN=−100 kN
,
V
4
=V
3
+R
B
=0
M
1
=−40 kN⋅1 m=−40 kN⋅m
,
M
2
=M
1
+80 kN⋅3 m=200 kN⋅m= M
max
,
M
3
=M
2
−100 kN⋅2 m=0
2
Z
required
=
1.67 M
σ
YS
=
1.67⋅200 kN⋅m
345 MPa
∣
MPa m
2
10
3
kN
∣
(10
3
mm)
3
m
3
=968×10
3
mm
3
From Appendix D, the best choice is
W460×52 which has a plastic section modulus of 1090×10
3
mm
3
and a mass per unit length of 52 kg/m. Multiply by
gravity to get the weight per unit length,
w =
52 kg
m
9.81 m
s
2
∣
N s
2
kg m
∣
kN
10
3
N
=0.510
kN
m
4 Add beam weight to the load
diagram, then draw an Equivalent Load
Diagram to find the reactions.
The equivalent point load for the beam
weight per unit length is
W =w⋅L=
0.510 kN
m
6 m
=3.06 kN
It acts at the center of the beam, 2 m to the right of reaction R
A
. Use Sum of the Moments and Sum of the Forces to find the
reaction forces.
R
B
=
−40 kN ⋅1 m+3.06 kN⋅2 m+180 kN ⋅3 m
5 m
=101.2 kN
R
A
=40 kN+3.06 kN+180 kN−101.2 kN=121.8 kN
106
A B
R
A
R
B
40 kN
Applied load + beam weight
1 m 2 m
180 kN
3 m
w
beam
= 0.510 kN/m
A B
R
B
40 kN
1 m
2 m
180 kN
3 m
W= 3.06 kN
5 m
R
A
A B
R
A
= 120 kN
V
V
4
= 0
V
3
= -100 kN
M
2
= 200 kN∙m
M
R
B
= 100 kN
40 kN
Applied load only
1 m 2 m
180 kN
3 m
V
2
=80 kN
V
1
=-40 kN
M
1
= -40 kN∙m
M
3
= 0

Chapter 11: Beam Design
!%
Now draw the shear and moment diagrams
V
1
=−40 kN
V
2
=V
1
−0.51
kN
m
⋅1 m=−40.5kN
V
3
=V
2
+R
A
=81.3 kN
V
4
=V
3
−0.51
kN
m
⋅3m=79.8kN
V
6
=V
5
−0.51
kN
m
⋅2 m=−101.2 kN
V
5
=V
4
−180 kN=−100.2 kN
V
7
=V
6
+R
B
=0
M
1
=−
(
40 kN+40.5 kN
2
)
⋅1 m=−40.3 kN⋅m
M
2
=M
1
+
(
81.3 kN+79.8 kN
2
)
⋅3 m=201.4 kN⋅m
M
3
=M
2
−
(
100.2 kN+101.2 kN
2
)
⋅2 m=0
Z
required
=
1.67 M
σ
YS
=
1.67⋅201.4 kN⋅m
345 MPa
∣
MPa m
2
10
3
kN
∣
(10
3
mm)
3
m
3
=975×10
3
mm
3
We have
Z
beam
=1090×10
3
mm
3
Since
Z
beam
>Z
required
, the beam is OK in bending.
9 The beam will support a shear load of
0.4 σ
YS
d t
w
=
0.4 345MPa 450 mm 7.62mm
∣
10
3
kN
MPa m
2
∣
m
2
(10
3
mm)
2
=473 kN
Since we are applying only 101.2 kN in
shear, the beam is OK in shear.
107
A B
R
A
V
V
7
= 0
V
6
= -101.2 kN
M
2
= 201.4 kN∙m
M
R
B
40 kN
Applied load + beam weight
1 m 2 m
180 kN
3 m
V
4
=79.8 kN
V
1
=-40 kN
M
1
= -40.3 kN∙m
M
3
= 0
w
beam
= 0.510 kN/m
V
2
=-40.5 kN
V
3
=81.3 kN
V
5
=-100.2 kN

Chapter 11: Beam Design
1
Rectangular cross-section timber beam design is similar to wide-flange steel beam design, except we use section modulus S
instead of plastic section modulus Z. Otherwise, the steps are the same:
% Identify all applied loads and design constraints.
- Draw the load diagram and calculate the reactions. Draw an equivalent load diagram if necessary.
. Draw shear and moment diagrams, and calculate V
max
and M
max
.
2 Select the lightest beam from Appendix E that will support M
max
, or has enough stiffness to limit Δ
max
. The allowable
moment in a timber beam
M
allowable
=σ S
x
, so the required section modulus is
S
required
=
M
σ
allowable bending
. Solve for S
required
,
then find the lightest timber beam that has a slightly larger value of S.
If the maximum deflection is specified, write the equation for Δ
max
, solve it for I
required
, then find the lightest timber beam that
has a slightly larger value of I, just like we did for steel beams previously.
4 Add the beam weight to the load diagram, and recheck moment and deflection. You may have to draw completely
new shear and moment diagrams. If
S
beam
>S
required
, the beam is OK in bending, and if
I
beam
>I
required
, the beam is OK in
deflection. If either of these conditions is not met, pick a larger beam and recalculate.
9 Check shear. For rectangular cross-section timbers,
τ=
3V
2 A
. If
V
applied
<
2 A τ
allowable
3
, the beam is OK in shear.
3
The weight per unit length of a steel beam is the specific weight of steel (0.284 lb./in.
3
) times the cross-sectional area of the
beam. For metric sizes, the mass per unit length of a steel beam is the density of steel (7.85 g/cm
3
) times the cross-sectional
area of the beam. These values are listed in Appendix D.
With timber beams, the weight per unit length for a given timber size depends on the type of wood, because different wood
species have different specific weights. Appendix E lists the weight per unit length for three different specific weights: 20,
30, and 40 lb./ft.
3
. For metric sizes, the mass per unit length is listed for three densities: 320, 480, and 640 kg/m
3
. Douglas
fir has a specific weight of 30 lb./ft.
3
, therefore you can find the weight per unit length of a 2×6 Douglas fir timber in Table
E3: it is listed as 1.72 lb./ft. in the table.
What if your 2×6 is made of Southern yellow pine? Specific weight
γ=34 lb./ft.
3
, which is not in the table...so you need to
interpolate to find the weight per unit length w of this beam.
Here are the first few rows of Table E3:
Designation Width Depth Area Moment of
inertia
Section
modulus
Weight per unit
length
γ = 20 lb/ft.
3
Weight per unit
length
γ = 30 lb/ft.
3
Weight per unit
length
γ = 40 lb/ft.
3
b d A I
x
S
x
w w w
(in.) (in.) (in.
2
) (in.
4
) (in.
3
) (lb./ft.) (lb./ft.) (lb./ft.)
2×2 1.5 1.5 2.25 0.422 0.563 0.313 0.469 0.625
2×3 1.5 2.5 3.75 1.95 1.56 0.521 0.781 1.04
2×4 1.5 3.5 5.25 5.36 3.06 0.729 1.09 1.46
2×6 1.5 5.5 8.25 20.8 7.56 1.15 1.72 2.29
From the 2×6 row,
w=1.72 lb./ft.
for
γ=30 lb./ft.
3
and
w=2.29lb./ft.
for
γ=40 lb./ft.
3
. If you graph these values, you
can see that the ratio of
34
lb.
ft.
3
−30
lb.
ft.
3
40
lb.
ft.
3
−30
lb.
ft.
3
is equal to
w −1.72
lb.
ft.
2.29
lb.
ft.
−1.72
lb.
ft.
. The math is essentially the same as a similar triangles
calculation.
108

Chapter 11: Beam Design
Rewrite the equation to solve for the weight per unit length:
w =
[
34
lb.
ft.
3
−30
lb.
ft.
3
40
lb.
ft.
3
−30
lb.
ft.
3
]
(
2.29
lb.
ft.
−1.72
lb.
ft.
)
+ 1.72
lb.
ft.
= 1.95
lb.
ft.
Use the same method to find the mass per unit length for SI timbers, and be
sure to multiply by gravity to find the weight per unit length.
Interpolation is a good skill to develop because it is used in many other
technical fields, including physics, chemistry, heat transfer, fluid mechanics,
and thermodynamics.
!&
Select the lightest Southern yellow pine beam for this load and
deflects no more than 0.5 in. at the free end.
% Identify loads and design constraints.
P = 800 lb.
L = 14 ft.
b = 12 ft.
Δ
max
≤ 0.5 in.
σ
allowable bending
= 900 psi (from Appendix E)
τ
allowable
= 180 psi (from Appendix E)
E = 1700 ksi (from Appendix E)
γ = 34 lb./ft.
3
- Sove for reactions:
R
B
=P =800 lb.
and
M
max
=P b=800 lb. × 12 ft.=9600 ft.⋅lb.
. Draw shear and moment diagrams, and identify maximum
values:
V
max
=800 lb.
,
M
max
=9600ft.⋅lb.
2
S
required
=
M
σ
all.bending
=
9,600 ft.⋅lb. in.
2
900lb.
∣
12 in.
ft.
=128 in.
3
From Appendix F,
Δ
max
=
P b
2
6 E I
(3 L−b)
Rewrite to solve for
I
required
=
P b
2
6 E Δ
max
(3 L−b)=
800 lb.(12 ft.)
2
in.
2
6 1700 kip 0.5 in.
[3(14 ft.)−12 ft.]
∣
kip
10
3
lb.
∣
(12 in.)
3
ft.
3
=1171in.
4
Look in Appendix E for the lightest Douglas fir beam for which
S> S
required
and
I >I
required
. The lightest beam that meets
the section modulus criterion is a 4×16 beam, with
S=136in.
3
. However, this beam does not meet the moment of inertia
criterion. The lightest beam that meets both criteria is a 6×16 beam, with
S=220 in.
3
and
I =1710 in.
4
.
109
A B
V
V
max
= -800 lb.
b =12 ft.
M
R
B
= 800 lb.
P= 800 lb.
Applied load only
Applied load + beam weight, 4×16 timber
w
beam
= 11.12 lb./ft.
M
B
= 9,600 ft.lb.
L =14 ft.
M
max
= -9,600 ft.∙lb.
A B
V
V
max
= -956 lb.
M
R
B
= 956 lb.
P= 800 lb.
M
B
= 10,690 ft.lb.
M
max
= -10,690 ft.∙lb.
30 4034
2.292.29
1.72
2.29
w
Weight
per unit
length
(lb./ft.)
Specific weight (lb./ft.
3
)

Chapter 11: Beam Design
!&45
4 Add the beam weight to the load diagram, and redraw the shear and moment diagrams. Since the specific weight of
Southern yellow pine is
34 lb./ft.
3
, interpolation is necessary.
w =
[
34
lb.
ft.
3
−30
lb.
ft.
3
40
lb.
ft.
3
−30
lb.
ft.
3
]
(
23.7
lb.
ft.
−17.8
lb.
ft.
)
+ 17.8
lb.
ft.
= 20.2
lb.
ft.
Using the Method of Superposition, we can add the effects
of the point load and the distributed load to find the reaction
force and reaction moment.
R
B
=V
max
=P +w L=800 lb.+20.2lb./ft. × 14 ft.=1083 lb.
M
B
=M
max
=P b+
w
beam
L
2
2
=800 lb. × 12 ft.+
20.2lb.
ft.
(14 ft.)
2
2
=11,580ft.⋅lb.
S
required
=
M
σ
all. bending
=
10,690 ft.⋅lb. in.
2
900 lb.
∣
12in.
ft.
=143 in.
3
We have
S
beam
=220 in.
3
Since
S
beam
>S
required
, the beam is
OK in bending.
Using the Method of Superposition, we can add the effect of the beam weight to solve for I
required
. From Appendix F, the
maximum deflection due to a uniform distributed load on a cantilever beam is
Δ
max
=
w L
4
8 E I
, therefore
I
required
=
P b
2
6 E Δ
max
(3 L−b)+
w L
4
8 E Δ
max
=1171 in.
4
+
20.2 lb.(14 ft.)
4
in.
2
8 ft. 1700 kip 0.5 in.
∣
kip
10
3
lb.
∣
(12 in.)
3
ft.
3
=1368in.
4
We have
I
beam
=1710 in.
4
Since
I
beam
>I
required
, the beam is OK in deflection.
9 The beam supports a shear load of
2 A τ
allowable
3
=
2⋅85.3in.
2
3
175lb.
in.
2
=9,952 lb.
Since we are applying only 1,083
lb. in shear, the beam is OK in shear.
*A
Beams can be made of other shapes and materials: aluminum extrusions, laminated wood with a nonrectangular cross-
section, steel pipe, and so forth. If your beam is neither a wide-flange steel beam nor a rectangular cross-section timber
beam, follow these 6 steps (essentially the same as the Timber Beam process, except for Step 6).
% Identify all applied loads and design constraints.
- Draw the load diagram and calculate the reactions. Draw an equivalent load diagram if necessary.
. Draw shear and moment diagrams, and calculate V
max
and M
max
.
2 Select the lightest beam that will support M
max
, or has enough stiffness to limit Δ
max
. Solve for
S
required
=
M
σ
allowable
,
then find the lightest beam that has a slightly larger value of S.
110
Applied load + beam weight, 6×16 timber
W
beam
= 20.2 lb./ft.
A B
V
V
max
= -1083 lb.
M
R
B
= 1,083 lb.
P= 800 lb.
M
B
= 11,580 ft.lb.
M
max
= -11,580 ft.∙lb.

Chapter 11: Beam Design
If the maximum deflection is specified, write the equation for Δ
max
, solve it for I
required
, then find the lightest beam that has a
slightly larger value of I.
4 Add the beam weight to the load diagram, and recheck moment and deflection. If
S
beam
>S
required
, the beam is OK in
bending, and if
I
beam
>I
required
, the beam is OK in deflection. If either of these conditions is not met, pick a larger beam and
recalculate.
9 Check shear. For rectangular cross-sections, use
V
applied
<
2 A τ
allowable
3
as we did with timber beams. For all other
shapes, rewrite the General Shear Formula
τ=
V Q
I t
and use
V
applied
<
τ
allowable
I Q
t
. The allowable shear stress for timber is
given in Appendix E. Allowable shear stress for steel is
0.4 σ
YS
.
+,
#,C
Follow the 6-step method for steel W-beams, using
Z
required
=
1.67 M
σ
YS
and
V
applied
≤0.4 σ
YS
d t
w
.
Follow the 6-step method for timber beams, using
S
required
=
M
σ
allowable bending
and
V
applied
<
2 A τ
allowable
3
.
*
Follow the 6-step method for timber beams, using
S
required
=
M
σ
allowable
and
V
applied
<
τ
allowable
I Q
t
.
111
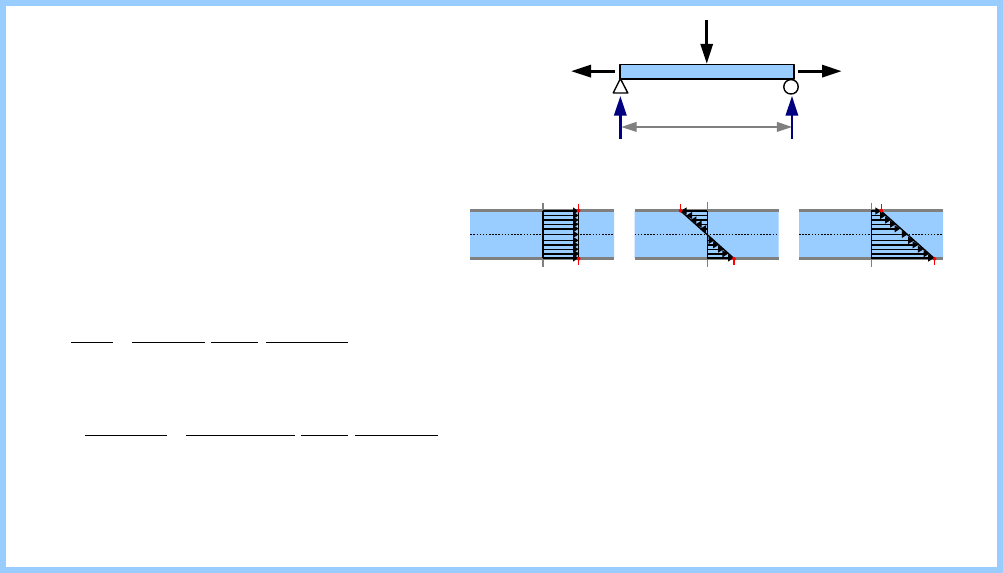
Chapter 12: Combined Stresses
%-&
E
Previous chapters discussed how to solve bending, torsion, tension, thermal, and pressure problems independently. Many
real problems combine states of stress: a steam pipe restrained at both ends (pressure + thermal stress), horizontal beams in
a tall building (vertical bending due to gravity + horizontal bending due to wind loads), or a bolt as it is tightened (torsion +
tension). We can use the Method of Superposition to solve these problems. Calculate the stresses at a given point due to
each loading condition, then add the stresses. We use the same method to calculate deflections.
!"
A 2 meter long, 51 mm diameter standard pipe is
loaded axially in tension with a load of 60 kN. The
bar is also a simply-supported beam, loaded
transversely at the midspan with a load of 250 kN.
Calculate the maximum stress in the bar. Report the
results in MPa.
Using the Method of Superposition, add the
maximum tensile stresses resulting from the axial
load and the bending load. The tensile stress in the
bar due to the axial load is
σ
axial
=
P
axial
A
=
60 kN
658 mm
2
∣
10
3
N
kN
∣
MPa mm
2
N
=91.2 MPa
From the Formula Method (Appendix F), the maximum bending stress due to the transverse load at the midspan is
σ
bending
=
P
transverse
L
4 S
=
250 kN ⋅2 m
4⋅8650mm
3
∣
10
3
N
kN
∣
MPa mm
2
N
=14.5MPa
.
The combined maximum stress is
σ
combined
=σ
axial
+σ
bending
=91.2MPa+14.5 MPa=105.6 MPa
. This maximum occurs on
the bottom side of the pipe at the midspan. (On the top side of the pipe at the midspan, the combined stress is
σ
combined
=σ
axial
−σ
bending
=91.2MPa−14.5 MPa=76.7 MPa
.)
#
Consider a square cross-section beam loaded vertically at the midspan: the maximum bending stress occurs on the top and
bottom surfaces. If the beam is loaded horizontally at the midspan, the maximum bending stress occurs on the side surfaces.
We can add the stresses at the corners to find the extremes.
The beam deflects down and to the left; we can calculate these deflections, then combine them using trigonometry.
112
+σ
bending
–σ
bending
Bending stress
A B
R
A
2 m
R
B
P
transverse
= 250 kN
P
axial
= 60 kN
σ
max
= σ
axial
+ σ
bending
Combined stress
+ =
+σ
axial
Axial stress
σ
min
= σ
axial
- σ
bending

Chapter 12: Combined Stresses
!#
A simply supported Douglas fir 2×4 timber is 84 in. long. It
has a vertical load of 50 lb. and a horizontal load of 30 lb. at
the midspan. Calculate the combined stresses at the edges of
the beam, at the midspan (in psi). Also calculate vertical,
horizontal, and total deflections (in inches).
From the Formula Method, the bending stress
at the midspan due to the vertical load is
σ
y
=
M
y
S
x
=
P
y
L
4 S
x
where S
x
is the section modulus about the x-x axis (listed in
Appendix E). This stress is positive (tension) at points C and
D, because they are on the far side of the beam from the
applied load.
The stress is negative (compression) at points A and B, because they are on the same side of the beam as the applied load.
σ
y
=
P
y
L
4 S
x
=
50 lb.⋅84in.
4⋅3.06 in.
3
=343 psi
, therefore
σ
y(C)
=σ
y (D)
=+343 psi
and
σ
y( A)
=σ
y( B)
=−343 psi
.
The bending stress at the midspan due to the horizontal load is
σ
x
=
M
x
S
y
=
P
x
L
4 S
y
. This stress is positive (tension) at points
A and C, negative (compression) at points B and D. Appendix E does not list S
y
for timber beams, so we have to calculate
it.
I
y
=
hb
3
12
=
3.5in.(1.5in.)
3
12
=0.984 in.
4
, therefore
S
y
=
I
y
c
=
I
y
(b/2)
=
0.984 in.
4
(1.5 in./2)
=1.313 in.
3
σ
x
=
P
x
L
4 S
y
=
30 lb. ⋅84 in.
4⋅1.313 in.
3
=480 psi
, therefore
σ
x(A)
=σ
x (C)
=+480 psi
and
σ
x(B)
=σ
x(D)
=−480 psi
.
The final step is to add the stresses at each location. The maximum tensile
stress is 823 psi at point C; the maximum compressive stress is -823 psi at
point B.
C From the Appendix, deflection due to a point load at the
midspan is
Δ
max
=
P L
3
48 E I
.
Vertical deflection is
Δ
vert.
=
P
y
L
3
48 E I
x
=
50 lb.(84 in.)
3
48
in.
2
1700 kips
5.36 in.
4
∣
kip
10
3
lb.
=0.068 in.
downward.
Horizontal deflection is
Δ
horiz.
=
P
x
L
3
48 E I
y
=
30lb. (84in.)
3
48
in.
2
1700 kips
0.984 in.
4
∣
kip
10
3
lb.
=0.221 in.
to the left.
Use trigonometry to find the combined deflection and its direction.
Δ
combined
=
√
Δ
horiz.
2
+Δ
vert.
2
=
√
(0.221 in.)
2
+(0.068 in.)
2
=0.231 in.
θ=tan
−1
Δ
vert.
Δ
horiz.
=tan
−1
0.068 in.
0.221 in.
=17.1°
113
Δ
horiz.
= 0.221 in.
Δ
vert.
= 0.068 in.
Δ
combined
θ
Point σ
y
(psi) σ
x
(psi) σ
total
(psi)
A −343 480 137
B −343 −480 −823
C 343 480 823
D 343 −480 −137
D
P
y
= 50 lb.
P
x
= 30 lb.
C
BA
D
B
A
P
y
= 50 lb.
P
x
= 30 lb.
x x
y
y
h
b

Chapter 12: Combined Stresses
"
Consider an axial member loaded in
tension or compression. If the load path
is not along the neutral axis, then a
bending moment develops in addition to
the axial load.
The weight of a traffic light hanging
from a cantilever arm creates an axial
stress
σ
axial
=−P / A
in the vertical
support pole (negative because the load
is compressive), while the weight times
the moment arm creates a bending
moment in the support pole, causing a
bending stress.
Moment is force times perpendicular distance; if we define this eccentric distance as e, the moment
M =P e
. The bending
stress at points A and B is
σ
bending
=±
M c
I
=±
P e c
I
. The combined stress in the pole is
σ
combined
=σ
axial
+σ
bending
=
−P
A
±
P e c
I
. At point A, the bending stress is compressive, so
σ
A
=
−P
A
−
P ec
I
. At point B, the
bending stress is tensile, so
σ
B
=
−P
A
+
P e c
I
.
Some problems that look like axial loading
problems are actually eccentric loading problems.
Consider this link in a conveyer belt chain. To find
the stresses at points A and B, cut the link as
shown. The total stress at these points is
σ
combined
=σ
axial
+σ
bending
=
P
A
±
P e c
I
where I is the moment of inertia in the link at the cut section.
A C-clamp or an arbor press is an eccentric load problem:
the frame is eccentrically loaded with respect to the
workpiece clamped between the anvils.
The cross-section of the body of a cast-iron C-clamp or
arbor press is not a rectangle, because cast iron is weaker in
tension than in compression. The inside surface of the
clamp is loaded in tension, therefore it needs more material
than the outside surface of the clamp. Calculate the moment
of inertia of a compound shape, find the neutral axis, and
determine two different values of c – one for the inside
surface, and the other for the outside surface. Eccentricity e
is the distance from the centerline of the clamp screw to the
neutral axis of the clamp body.
114
P
Axial
stress
e
c
A B
+
Bending
stress
Combined
stress
=
R R
P
M = Pe
=
P
A
B
=
P
A
B
e
c
P
e
c
outside
c
inside
c
outside
c
inside
Cross-section

Chapter 12: Combined Stresses
Another type of eccentric load involves a
block of stone or concrete...a so-called short-
block problem. The block is short in
comparison with a masonry column.
Consider a short masonry block with a
vertical point load. If the load is centric, then
the stress at the base of the block is due to the
point load and the weight of the block:
σ=
−W
A
−
P
A
. Both terms are negative
because they are both compressive loads.
If the load is offset from the center, we have
an eccentric load problem. The combined
stress at the base of the block is the axial term
plus the bending moment term. The weight (a
centric load) adds to the axial term, but not to
the bending moment term.
The combined stress at the base of an
eccentrically loaded short block is
σ=
−W
A
−
P
A
±
P e c
I
y
where
I
y
=
b d
3
12
.
See Example #3 for a worked-out problem with numbers and units.
We can modify this short block problem by shifting the point load so it is
eccentric with respect to both the x-x and y-y neutral axes. Use the same
technique as before, but add another term for the new eccentricity:
σ=
−W
A
−
P
A
±
P e
1
c
1
I
y
±
P e
2
c
2
I
x
where
I
y
=
bd
3
12
and
I
x
=
d b
3
12
. Now
the short block problem starts to look like an Accounting problem. The
way this block is drawn, eccentricity e
1
will create a positive stress as A
and C, a negative stress at B and D. Eccentricity e
2
will create a positive
stress as C and D, a negative stress at A and B. The maximum
compressive stress occurs at point B because the bending stresses due to
both eccentricities are negative at that corner; the maximum tensile stress
(or smallest compressive stress, if we don't achieve tension) is at point C,
because the bending stresses due to both eccentricities are positive at that
corner.
See Example #4 for a worked-out problem with numbers and units.
115
P
W
d
c
1
b
x x
y
y
e
2
e
1
c
2
A
B
D
C
Centric loading
P
R
P
R
e
Eccentric loading
W
W
d c
b
Axial
stress
+
Bending
stress
=
Combined
stress
x
x
y
y
x x
y
y
Axial stress

Chapter 12: Combined Stresses
!$
A stone block measuring 2.5 ft. × 4 ft. × 3 ft. has an eccentric
load of 12 kips placed 1.5 ft. to the right of center as shown.
The specific gravity of the stone is 200 lb./ft.
3
. Calculate the
stresses at corners A, B, C, and D. Report the results in psi.
Weight is specific weight times volume:
W =γ V =
200lb.
ft.
3
2.5ft.×4 ft.×3ft.
∣
kip
10
3
lb.
=6 kips
.
Axial stress due to the weight is
σ
W
=
−W
A
=
−6 kips
2.5 ft.×4 ft.
∣
10
3
lb.
kip
∣
ft.
2
(12 in.)
2
=−4.17 psi
Axial stress due to the point load is
σ
P
=
−P
A
=
−12 kips
2.5ft.×4 ft.
∣
10
3
lb.
kip
∣
ft.
2
(12 in.)
2
=−8.33 psi
The moment of inertia of the plan-view of the block with
respect to the y-y axis is
I
y
=
b d
3
12
=
2.5ft. (4 ft.)
3
12
=13.3ft.
4
Bending stress due to the eccentric load is
σ
bending
=±
P e c
I
y
=±
12 kips⋅1.5ft.⋅2ft.
13.3ft.
4
∣
10
3
lb.
kip
∣
ft.
2
(12 in.)
2
=±18.75 psi
This stress is positive (tension) at points A and C, negative
(compression) at points B and D.
Create a table to add up the stresses. Along the left edge of
the block, the stress is 6.25 psi in tension; along the right
edge, the stress is 31.25 psi in compression.
In a masonry structure, tensile stress leads to cracks because stone and
unreinforced concrete tend to be many times stronger in compression
than in tension. One type of short block problem is to find the optimum
location of P such that no tensile stress develops. We want the stress at
the left edge of this diagram to equal zero, so
σ=0=−
W
A
−
P
A
+
P e c
I
y
.
Rewrite the equation to solve for e, then calculate the answer.
116
Axial
stress
+
Bending
stress
=
Combined
stress
σ = 0
Point σ
W
(psi) σ
P
(psi) σ
bending
(psi) σ
total
(psi)
A −4.17 −8.33 18.75 6.25
B −4.17 −8.33 −18.75 −31.25
C −4.17 −8.33 18.75 6.25
D −4.17 −8.33 −18.75 −31.25
P = 12 kips
W
d = 4 ft.
Axial
stress
+
Bending
stress
=
Combined
stress
A
B
D
C
h = 3 ft.
b = 2.5 ft.
c = 2 ft.
x x
y
y
e = 1.5 ft.

Chapter 12: Combined Stresses
!%
The stone block from Example #3 has an eccentric load of
12 kips placed 1.5 ft. to the right of center and 0.5 ft. to the
front of center. Calculate the corner stresses in psi.
Axial stress due to the weight and the point load
are the same as before:
σ
W
=−4.17 psi
and
σ
P
=−8.33 psi
. The moment of inertia with respect to the
y-y axis is the same as before:
I
y
=
b d
3
12
=13.3ft.
4
The
moment of inertia with respect to the x-x axis is
I
x
=
d b
3
12
=
4ft.(2.5 ft.)
3
12
=5.21 ft.
4
.
Bending stress due to eccentricity e
1
is the same as before:
σ
bending 1
=±
P e
1
c
1
I
y
=±
12 kips⋅1.5 ft.⋅2 ft.
13.3 ft.
4
∣
10
3
lb.
kip
∣
ft.
2
(12 in.)
2
=±18.75 psi
. Bending stress due to eccentricity e
2
is
σ
bending 2
=±
P e
2
c
2
I
x
=±
12 kips ⋅0.5 ft.⋅1.25ft.
5.21 ft.
4
∣
10
3
lb.
kip
∣
ft.
2
(12 in.)
2
=±10 psi
.
Create a table to add up the stresses. The
maximum compressive stress is at the front right
corner; the rear left is the only corner with a
tensile stress.
Solve a short-block problem in SI units the same way, except you will have to convert mass to weight:
W =mg
. For
example, if a granite block measures 1 m by 0.8 m by 0.6 m, the weight is
W =mg =ρV g=
2.69g
cm
3
1m×0.8 m×0.6 m 9.81 m
s
2
∣
N s
2
kg m
∣
kN
10
3
N
∣
(100cm)
3
m
3
∣
kg
10
3
g
=12.7 kN
+,
Combine stresses due to multiple loads by adding the individual stresses.
Solve short block problems with
σ=
−W
A
−
P
A
±
P e
1
c
1
I
y
±
P e
2
c
2
I
x
where
I
x
=
d b
3
12
and
I
y
=
bd
3
12
117
Point σ
W
(psi) σ
P
(psi) σ
bending 1
(psi) σ
bending 2
(psi) σ
total
(psi)
A −4.17 −8.33 +18.75 −10.00 −3.75
B −4.17 −8.33 −18.75 −10.00 −41.25
C −4.17 −8.33 +18.75 +10.00 +16.25
D −4.17 −8.33 −18.75 +10.00 −21.25
P = 12 kips
W
x x
y
y
e
1
= 1.5 ft.
c
2
= 1.25 ft.
A
B
D
C
d = 4 ft.
h = 3 ft.
b = 2.5 ft.
c
1
= 2 ft.
e
2
= 0.5 ft.

Chapter 13: Statically Indeterminate Beams
%.&
!
We know how to calculate deflection, reactions,
shear stresses, and bending stresses in beams that
have two reactions (either two reaction forces, or a
reaction force and a reaction moment). These
problems have two unknowns and two equations
(sum of the moments, sum of the forces). Since the
number of unknowns equals the number of
equations, we can solve the problems directly with
simple algebra, and we call these problems statically
determinate.
From a design perspective, a statically determinate
structure is risky; if one of the supports fails, the
entire structure collapses. If you are building a deck,
adding extra supports will preserve the deck even if
one support is damaged. However, each additional
support adds an unknown without adding an
equation, so we cannot solve the problem directly; it
is a statically indeterminate beam.
'
We can split a statically indeterminate problem into two statically determinate problems. Consider a propped cantilever
beam: if we remove the prop, the end of the beam deflects downward by an amount
Δ
1
. If instead we remove the applied
load and leave the prop in place, reaction force R
A
causes the end of the beam to deflect upward by an amount
Δ
2
. Since
the end of the propped cantilever beam is a simple support and does not deflect,
Δ
1
=Δ
2
. Use the Formula Method to find
expressions for deflection, set them equal, and solve for reaction force R
A
.
6
% Identify the location of the extra support, having a force reaction only (no moment reaction).
- Remove the extra support from the original load diagram, and find the deflection formula in Appendix F for the
location you selected in Step 1.
. Remove the applied loads from the original load diagram and find the deflection formula in Appendix F for the same
location used in Step 2.
2 Set the deflection formulas equal to each other, and solve for the unknown reaction force.
4 Use sum of the forces and sum of the moments to find the remaining beam reactions.
118
P
R
B
M
B
P
R
B
R
A
A B A B
P
R
B
M
B
P
R
B
R
A
A B A B
R
C
C
R
A
Statically determinate beams
Statically indeterminate beams
P
A B
Elastic
curve
Δ
1
C
R
B
M
B
R
A
+=
A B
R
B
M
B
Elastic
curve
Δ
2
P
A BC
R
B
M
B
R
A
C

Chapter 13: Statically Indeterminate Beams
!"
A propped 8 foot long cantilever beam has an applied load of 3 kips located 2 feet from the prop. Calculate the reaction
forces and reaction moment. Report the results in kips and kip⋅ft., respectively.
% Select the free end of the beam (Point *) for the deflection location.
- Remove support R
A
. From Appendix F, the deflection at Point * due to the applied load P is
Δ
1
=
P b
2
6 E I
(3 L−b)
.
. Restore support R
A
and remove the applied load P. From Appendix F, the deflection at Point * due to a point load at
the free end is
Δ
2
=
P L
3
3 E I
. However, the point load P in this equation is actually R
A
, so
Δ
2
=
R
A
L
3
3 E I
.
2 Set the deflection equations equal to each other:
Δ
1
=Δ
2
=
P b
2
6 E I
(3 L−b)=
R
A
L
3
3 E I
. Young's modulus and moment
of inertia cancel, so the solution is independent of the cross-sectional shape and material of the beam:
P b
2
6
(3 L−b)=
R
A
L
3
3
. Divide both sides by 3 to get
P b
2
2
(3 L−b)=R
A
L
3
. Solve for the reaction force,
R
A
=
P b
2
2 L
3
(3 L−b)=
3 kips(6ft.)
2
2(8 ft.)
3
(
3(8 ft.)−6ft.
)
=1.90 kips
4 Sum of the Forces gives us
R
B
=P−R
A
=3.00 kips−1.90 kips=1.10 kips
Sum of the Moments gives us
M
B
=P⋅b−R
A
⋅L=3.00 kips⋅6ft.−1.90 kips⋅8 ft.=2.80kip⋅ft.
119
P = 3 kips
A B
b = 6 ft.
a = 2 ft.
Elastic
curve
Δ
1
C
R
B
M
B
R
A
+=
A B
L = 8 ft.
R
B
M
B
Elastic
curve
Δ
2
P = 3 kips
A B
b = 6 ft.
2 ft.
C
R
B
M
B
R
A
C

Chapter 13: Statically Indeterminate Beams
!#
A 3 meter long beam has an applied load of 300 kN located at the midspan. The beam is supported at the ends and with a
third support 1 meter from the right end. Calculate the three reaction forces. Report the results in kN.
% Select location for the deflection location.
- Remove support R
C
. From Appendix F, the deflection at Point due
to the applied load P at the midspan is
Δ
1
=
P x
48 E I
[
3 L
2
−4 x
2
]
for
x<
L
2
.
Since
x=2 m>
L
2
, we have to flip the diagram, so
x=1 m
, measured
from the other end.
. Restore support R
C
and remove the applied load P. From Appendix
F, the deflection at Point due to a point load at Point is
Δ
2
=
P a
2
b
2
3 E I L
.
However, the point load P in this equation is actually R
C
, so
Δ
2
=
R
C
a
2
b
2
3 E I L
.
2 Set the deflection equations equal to each other:
Δ
1
=Δ
2
=
P x
48 E I
[
3 L
2
−4 x
2
]
=
R
C
a
2
b
2
3 E I L
. Once again, E and I
cancel. Solving, we get
R
C
=
P x L
16 a
2
b
2
[
3 L
2
−4 x
2
]
=
300 kN⋅1 m⋅3 m
16 (2 m)
2
(1 m)
2
[
3(3 m)
2
−4(1 m)
2
]
=323.4 kN
4 Sum of the Moments about point * gives us
M
B
=0=−300 kN⋅1.5 m+323.4 kN⋅2 m+R
B
⋅3 m
. Solve for
R
B
=
300 kN⋅1.5 m−323.4 kN⋅2m
3m
=−65.6 kN
. The negative sign means R
B
acts downward.
Sum of the Forces gives us
R
A
=P− R
B
−R
C
=300 kN−(−65.6 kN)−323.4 kN=42.2 kN
, positive, therefore acting
upward.
Once you have solved for the reactions, you can draw shear and moment diagrams to find maximum bending and shear
stresses.
120
Elastic
curve
Δ
1
=
Elastic
curve
Δ
2
R
B
R
A
A B
R
C
C
P = 300 kN
R
B
R
A
A B
R
B
R
A
A B
R
C
C
1 m1.5 m
3 m
P = 300 kN
b = 1 m
L = 3 m
a = 2 m
+
C
x = 2 m
L/2 L/2
Elastic
curve
Δ
1
R
A
R
B
B A
P = 300 kN
C
x = 1 m
L/2 L/2
Flipped diagram

Chapter 13: Statically Indeterminate Beams
!$
Calculate the maximum bending and shear stresses for Example
#2, assuming a Southern yellow pine 250×560 timber. Ignore the
weight of the beam. Report the results in MPa.
Calculate the values on the shear diagram values as
follows:
V
1
=R
A
=42.2 kN
V
2
=V
1
−300 kN=−257.8 kN
V
3
=V
2
+323.4 kN=65.6 kN
V
4
=V
3
−65.6kN=0 kN
Calculate the values on the moment diagram as follows:
M
1
=42.2 kN×1.5 m=63.3 kN⋅m
M
2
=M
1
−257.8 kN×0.5 m=−65.6 kN⋅m
M
3
=M
2
+65.6 kN×1m=0 kN⋅m
The maximum moment, 65.6 kN⋅m, is at point . The maximum
bending stress is
σ=
M
S
=
65.6 kN⋅m
12.0×10
6
mm
3
∣
(10
3
mm)
3
m
3
∣
MPa m
2
10
3
kN
=5.47MPa
,
which is less than the allowable 9.65 MPa for Southern yellow pine, therefore the beam is OK in bending.
The maximum shear load is 257.8 kN, just to the right of the point load. The maximum shear stress for a rectangular cross-
section is
τ=
3 V
2 A
=
3⋅ 257.8 kN
2⋅132×10
3
mm
2
∣
(10
3
mm)
2
m
2
∣
MPa m
2
10
3
kN
=2.93 MPa
, which is more than the 1.21 MPa allowable for
Southern yellow pine, therefore the beam will fail in shear.
Each of these examples shows a single point load. If there is more than one point load, set up the problem by removing a
support, then by removing the applied loads. Otherwise, the solution is the same as before.
121
R
B
= 65.6 kNR
A
= 42.2 kN
A BC
P = 300 kN
1 m1.5 m
3 m
V
1
= 42.2 kN
V
V
4
= 0 kN
V
2
= -257.8 kN
V
3
= 65.6 kN
M
M
3
= 0 kN⋅m
R
C
= 323.4 kN
M
1
= 63.3 kN⋅m
M
2
= -65.6 kN⋅m
Elastic
curve
Δ
1
=
Elastic
curve
Δ
2
R
B
R
A
A B
R
C
C
P
R
B
R
A
A B
R
B
R
A
A B
R
C
C
P PP
+
C

Chapter 13: Statically Indeterminate Beams
Distributed load problems are solved the same way.
!%
A 12 foot long 8×8 hem-fir timber beam has a nonuniform applied load as
shown. The beam is supported at the ends and with a third support at the
midspan. Calculate the three reaction forces due to the applied load and the
weight of the beam. Report the results in pounds.
Calculate the weight per unit length of the beam. Since the specific
weight of hem-fir is
25 lb./ft.
3
, interpolation is necessary.
w =
[
25
lb.
ft.
3
−20
lb.
ft.
3
30
lb.
ft.
3
−20
lb.
ft.
3
]
(
11.7
lb.
ft.
−7.81
lb.
ft.
)
+ 7.81
lb.
ft.
= 9.76
lb.
ft.
Now the beam has two loads: the applied nonuniform distributed load plus
the beam weight. Each load will create its own elastic curve.
122
Elastic
curve
Δ
1
=
Elastic
curve
Δ
2
R
B
R
A
A B
R
C
C
R
B
R
A
A B
R
B
R
A
A B
R
C
C
w
w
+
C
R
B
R
A
A B
R
C
C
200 lb./ft.
6 ft.
6 ft.
R
B
R
A
A B
R
C
C
200 lb./ft.
9.76 lb./ft.
Δ
2
+
Elastic
curve
Δ
3
R
B
R
A
A BC
R
B
R
A
A B
R
B
R
A
A B
R
C
C
9.76 lb./ft.
+
200 lb./ft.
C
x = 6 ft.
=
Δ
1
Elastic curve Elastic curve
midspan
midspan

Chapter 13: Statically Indeterminate Beams
!%
% Select location for the deflection location.
- Remove support R
C
. From Appendix F, the deflection at the midspan due to the weight of the beam is
Δ
1
=
5 w
beam
L
4
384 E I
, and the deflection at any location x due to the nonuniform distributed load is
Δ
2
=
w
max
x
360 E I L
(3 x
4
−10 L
2
x
2
+7 L
4
)
, so the total deflection due to the loads is
Δ
1+2
=
5w
beam
L
4
384 E I
+
w
max
x
360 E I L
(3 x
4
−10 L
2
x
2
+7 L
4
)
. At the midspan,
x=
L
2
, so the deflection equation simplifies to
Δ
1+2
=
5w
beam
L
4
384 E I
+
w
max
L
360 E I L 2
(
3
(
L
2
)
4
−10 L
2
(
L
2
)
2
+7 L
4
)
=
5 w
beam
L
4
384 E I
+
15 w
max
L
4
2304 E I
.
. Restore support R
C
and remove the applied nonuniform distributed load. From Appendix F, the deflection is
Δ
3
=
P L
3
48 E I
where P is R
C
.
2 Set the deflection equations equal to each other:
R
C
L
3
48 E I
=
5w
beam
L
4
384 E I
+
15 w
max
L
4
2304 E I
. Terms L
3
, E and I cancel. Solving
for the reaction, we get
R
C
=48
[
5w
beam
L
384
+
15 w
max
L
2304
]
=48
[
5 9.76 lb.12 ft.
384 ft.
+
15 200 lb.12 ft.
2304 ft.
]
=823 lb.
Use an Equivalent Load Diagram and Sum of the Moments to find the
reaction R
B
; use Sum of the Forces to find reaction R
A
.
R
B
=
117 lb.×6 ft.−823lb.×6 ft.+1200 lb.×8ft.
12 ft.
=447 lb.
R
A
=(117+1200−823−447)lb.=47 lb.
+,
Use the Method of Superposition to solve statically indeterminate beam problems.
123
R
B
R
A
A B
R
C
C
1200 lb
12 ft.
6 ft.
117 lb
8 ft.

Chapter 14: Buckling of Columns
%2&
Squeeze a short cylindrical block
elastically, and the normal stress
is
σ=P / A
. Squeeze hard
enough to exceed the yield
strength, and the block will either
fail by distorting (if it is ductile)
or by fracturing (if it is brittle). A
ductile short block will yield at
the same load, whether it is in
tension or in compression.
Change the dimensions of the
cylinder so it is very long and
thin, and push on the ends: it will
form a gentle bow at a normal
stress less than the yield strength of the material. We call this a slender column. You
can make a slender column by cutting out the longest straight segment of a steel wire coat
hanger. Put one end on a kitchen scale and press on the other end; the wire will bow under a
force of a couple of pounds. If we measure a wire diameter of 0.087 in. and assume a yield
strength of 30 ksi, the wire will not yield in tension until the load reaches
P
tension
=σ A=
30 kips
in.
2
π(0.087 in.)
2
4
∣
10
3
lb.
kip
=178 lb.
In tension, it takes almost 200 lb. to permanently
deform the wire, while in compression it takes about 2 lb. – a difference of two orders of magnitude! The extreme example
of a slender column is a rope or cable: high tensile strength; no compressive strength.
Between the short block and the slender column is the intermediate column, not as skinny as the slender column, but longer
and thinner than the short block. Push on the ends, and an intermediate column forms a kink about halfway up, at a normal
stress less than the yield strength of the material. You can make an intermediate column with a thick piece of solder about
10 in. long.
Leonhard Euler, the Swiss mathematician who gave us the e
x
button on the calculator, studied the
mathematics of columns. He derived an equation for the critical load that causes buckling in an ideal
slender column that is pinned at both ends. The Euler critical load
P
cr
=
π
2
E I
L
2
where I is the smallest
moment of inertia for the cross-sectional area of the column. For example, if the column is a wide-flange
beam,
I
y
<I
x
, so use I
y
. Euler's equation tells us the critical load for a 16.5 in. long coat hanger wire is
P
cr
=
π
2
E I
L
2
=
π
2
E
L
2
π d
4
64
=
π
2
(16.5in.)
2
30×10
6
lb.
in.
2
π( 0.087in.)
4
64
=3.1 lb.
, which is pretty close to, but not the
same as, the 2 lb. measured in the kitchen. Why are the numbers different? Euler's equation assumes the
wire is perfectly straight, the loads are applied in perfect alignment with the axis of the column, there are
no materials defects in the steel, the cross-section is perfect and uniform along the length of the wire, there
are no scratches on the wire's surface, and the ends can rotate freely with no friction.
124
P
P
σ < σ
YS
P
Short block
P
P
Slender
column
P
P
Intermediate
column
σ > σ
YS
ductile
failure
σ > σ
YS
brittle
failure
σ < σ
YS
bow
σ < σ
YS
kink
P
cr
L

Chapter 14: Buckling of Columns
What if you know the applied load, and have to select a solid round rod to support that load? Rewrite the Euler critical load
equation, solving for diameter:
P
cr
=
π
2
E I
L
2
=
π
2
E
L
2
π d
4
64
→ d =
4
√
64 P L
2
π
3
E
.
!"
An aluminum column made of 2 cm square barstock is loaded as a pin-connected
column. Calculate the Euler critical load for this column if the length is 3 m. Report the
result in kN.
The moment of inertia of a solid square is
I =
bh
3
12
=
b
4
12
.
From Appendix B, E = 70 GPa.
P
cr
=
π
2
E I
L
2
=
π
2
b
4
E
12 L
2
=
π
2
(2cm)
4
70 GPa
12 (3m)
2
∣
10
6
kN
GPa m
2
∣
m
4
(100cm)
4
=1.02kN
Recall the definition for radius of gyration of an area:
r
G
=
√
I / A
. Square both sides to get
r
G
2
=I /A
. The Euler critical
load divided by the cross-sectional area of the column gives us the stress in the column:
P
cr
A
=σ
cr
=
π
2
E I
L
2
A
=
π
2
E r
G
2
L
2
=
π
2
E
(L/ r
G
)
2
. The quantity L/r
G
is called the slenderness ratio of the column; the larger this value,
the more slender the column.
The end of a column can have one of three
support conditions. It can be pinned: free to
rotate, but prevented from sliding sideways. It
can be fixed, like the wall-end of a cantilever
beam: prevented from rotating or sliding. It can
be free to rotate and slide, like the free end of a
cantilever beam.
If both ends are pinned, the column bows in an
arc equal to the length of the column. The
effective length of the column is its own length.
If both ends are fixed, then the column cannot
rotate at its ends. It bows in the center relative to
two inflection points located L/4 from each end,
so the effective length of the bow is half the
column length, and
L
eff
=0.5 L
.
If one end is fixed while the other is pinned, then
the column can rotate about the pinned connection. The column bows over an effective length
L
eff
=0.7 L
.
A fixed & free column looks like a flagpole; a pteranodon landing on the tip will cause the flagpole to
sway. The column bows over an effective length that is twice its actual length:
L
eff
=2 L
.
125
Pinned
K = 1
Fixed
K = 0.5
Fixed & pinned
K = 0.7
Fixed & free
K = 2
L
eff
=0.5 LL
eff
= L
L
eff
=0.7 L
L
eff
=2 L
P
cr
P
cr
P
cr
P
cr
P
cr
3 m
2 cm
2 cm
cross
section

Chapter 14: Buckling of Columns
We can modify Euler's critical load equation to include these support conditions:
P
cr
=
π
2
E I
(KL)
2
where K is the effective
length factor 1, 0.5, 0.7, or 2, as appropriate. Likewise, the Euler stress is
σ
cr
=
π
2
E
(KL/ r
G
)
2
.
These equations help us find the load and stress when buckling first starts, assuming perfect loading conditions and
materials. In real life, we need to include a Factor of Safety, so
P
cr
=
π
2
E I
(KL)
2
F.S.
and
σ
cr
=
π
2
E
(KL/ r
G
)
2
F.S.
.
!#
A standard 4 inch pipe 35 feet long is used as an Ideal fixed column. Using a factor of
safety of 2, calculate the load that the pipe can support; report the result in kips. Calculate
the stress in the pipe; report the result in ksi.
Since the column is fixed,
K=0.5
. From Appendix D, a standard 4 inch pipe
has a moment of inertia
I =6.82 in.
4
, a radius of gyration
r
G
=1.51 in.
, and a cross-
sectional area of 2.96 in.
2
.
P
cr
=
π
2
E I
(KL)
2
F.S.
=
π
2
(0.5⋅35 ft.)
2
2
30×10
6
lb.
in.
2
6.82 in.
4
∣
kips
10
3
lb.
∣
(ft.)
2
(12 in.)
2
=24.3kips
σ
cr
=
π
2
E
(
KL
r
G
)
2
F.S.
=
π
2
(
0.5 ⋅35ft.
1.51 in.
∣
12 in.
ft.
)
2
⋅2
30×10
6
lb.
in.
2
∣
kips
10
3
lb.
=7.65 ksi
W-beams are often used as columns in steel structures. AISC recommends using the following formulas for calculating the
allowable load. A factor of safety is built in to the equations.
If
KL
r
G
>200
then the column is too slender for safe use; stop all calculations, and pick a shorter or deeper column.
If
KL
r
G
>4.71
√
E
σ
YS
then
P
all
=0.525σ
cr
A
If
KL
r
G
<4.71
√
E
σ
YS
then
P
all
=
0.658
(σ
YS
/σ
cr
)
σ
YS
A
1.67
Solve Structural Steel Column problems in four steps:
% Calculate
KL/r
G
and
4.71
√
E/σ
YS
. Since
r
Gy
<r
Gx
for W-beams, use r
Gy
- Calculate σ
cr
. Use the appropriate formula to calculate P
all
2 Use
σ=P
all
/ A
to find the stress in the column
126
cross
section
35 ft.
P
cr

Chapter 14: Buckling of Columns
!$
A 30 m long W200×59 wide-flange beam made from A36 steel is used as a fixed and pinned
column. Calculate the allowable load; report the result in kN. Calculate the stress in the column;
report the result in MPa.
Since the column is fixed and pinned,
K=0.7
. From Appendix D,
r
Gx
=89.7 mm
and
r
Gy
=51.8 mm
. Use the smaller of these numbers. From Appendix B, the yield strength of A36
steel is 250 MPa.
KL
r
G
=
0.7⋅30 m
51.8mm
∣
10
3
mm
m
=405
Since
KL
r
G
>200
, the column is too slender for safe use.
!%
Solve Example #3 using a 12 m long W200×59 wide-flange beam.
The material and dimensional properties are the same as in Example #3.
KL
r
G
=
0.7⋅12 m
51.8mm
∣
10
3
mm
m
=162.2
4.71
√
E
σ
YS
=4.71
√
207 GPa
250 MPa
∣
10
3
MPa
GPa
=136
Since
KL
r
G
>4.71
√
E
σ
YS
, use
P
all
=0.525σ
cr
A
where
σ
cr
=
π
2
E
(KL/r
G
)
2
. We can plug in the
calculated value of KL/r
G
from above.
σ
cr
=
π
2
207 GPa
(162.2)
2
∣
10
3
MPa
GPa
=77.7 MPa
P
all
=0.525σ
cr
A=
0.525⋅77.7 MPa⋅7550 mm
2
∣
10
3
kN
MPa m
2
∣
m
2
(10
3
mm)
2
=308 kN
The actual stress in the column is
σ=
P
all
A
=
308kN
7550mm
2
∣
MPa m
2
10
3
kN
∣
(10
3
mm)
2
m
2
=40.8MPa
'
Structural columns are large – several feet to dozens of feet tall. Machines also use long, thin compression members, such as
connecting rods in internal combustion engines. If
KL
r
G
≥
√
2π
2
E
σ
YS
then the column is slender, and the allowable stress is
σ
all
=
π
2
E
(KL/r
G
)
2
F.S.
. This is the Euler equation for ideal columns.
127
12 m
P
cr
30 m
P
cr

Chapter 14: Buckling of Columns
On the other hand, if
KL
r
G
<
√
2π
2
E
σ
YS
then the column is intermediate. Based on empirical data from real machine parts, J.B.
Johnson developed a formula for the allowable stress:
σ
all
=
[
1−
σ
YS
(KL/ r
G
)
2
4 π
2
E
]
σ
YS
F.S.
.
Calculate the allowable load of a steel machine part by multiplying the allowable stress by the cross-sectional area.
!&
A 20 inch long , 1 inch diameter steel rod with a yield strength of 35 ksi is used as a fixed and
pinned column with a Factor of Safety of 2. Calculate the allowable stress in the machine part;
report the result in ksi. Calculate the the allowable load in the machine part; report the result in
kips.
Since the column is fixed and pinned,
K=0.7
. The radius of gyration of a solid circle
is one quarter the diameter, so r
G
= 0.25 in.
KL
r
G
=
0.7⋅20 in.
0.25in.
=56
√
2π
2
E
σ
YS
=
KL
r
G
<
√
2 π
2
⋅30×10
3
ksi
35 ksi
=130
Since
KL
r
G
<
√
2π
2
E
σ
YS
, the column is intermediate.
σ
all
=
[
1−
σ
YS
(KL/ r
G
)
2
4 π
2
E
]
σ
YS
F.S.
=
[
1−
35 ksi (56)
2
4π
2
30×10
3
ksi
]
35 ksi
2
=15.9ksi
and
P
all
=σ
all
A=
15.9 kips
in.
2
π(1 in.)
2
4
=12.5 kips
Some machine design problems start with a known load and column length; your job is to calculate the minimum diameter
of a solid round rod to allow the column to survive buckling. Remember that the radius of gyration of a solid round rod is
d/4 and the allowable stress is
σ
all
=
P
A
=
P
(π/4)d
2
, then follow these six steps:
% Assume the column is slender (because the math is easier):
σ
all
=
π
2
E
(KL/r
G
)
2
F.S.
=
P
(π/4)d
2
- Rewrite the equation to solve for diameter.
. Check that the column really is slender.
2 If the column is not slender, then
σ
all
=
[
1−
σ
YS
(KL/ r
G
)
2
4 π
2
E
]
σ
YS
F.S.
=
P
(π/4)d
2
4 Rewrite the equation to solve for diameter. This is a little tricky because of the number of terms.
9 Check that the column really is intermediate; if it isn't, you made a mistake someplace.
If the cross-sectional area of the column is a different shape (such as a rectangle), follow these steps, using the appropriate
equations for area and r
G
.
128
20 in.
P
cr

Chapter 14: Buckling of Columns
+,
The Euler critical load is
P
cr
=
π
2
E I
(KL)
2
F.S.
, and the Euler critical stress is
σ
cr
=
π
2
E
(KL/ r
G
)
2
F.S.
If
KL
r
G
>200
then the column is too slender for safe use.
If
KL
r
G
>4.71
√
E
σ
YS
then
P
all
=0.525σ
cr
A
If
KL
r
G
<4.71
√
E
σ
YS
then
P
all
=
0.658
(σ
YS
/σ
cr
)
σ
YS
A
1.67
'
If
KL
r
G
≥
√
2π
2
E
σ
YS
then the column is slender, and the allowable stress is
σ
all
=
π
2
E
(KL/r
G
)
2
F.S.
.
If
KL
r
G
<
√
2π
2
E
σ
YS
then the column is intermediate, and
σ
all
=
[
1−
σ
YS
(KL/r
G
)
2
4 π
2
E
]
σ
YS
F.S.
.
Calculate
P
all
=σ
all
A
To find the smallest allowable diameter of a round solid rod, follow the 6-step procedure described above.
129

Chapter 15: Visualizing Stress and Strain
%4&38
'
We can see deformation, if it's large enough, but we cannot see stress, and in most cases we cannot measure it directly.
Instead, we can use a strain gauge to measure the strain on the surface of an object that is being elastically deformed, and
use Young's Modulus to estimate the stress.
The earliest strain gauges in the 1930s were made of fine
wire. If you glue a very thin wire along the bottom
surface of a beam, then load the beam in bending, the
wire will stretch and become thinner. The thinner the
wire becomes, the higher its electrical resistance. By
measuring this resistance you can determine strain, then
calculate stress as
σ=
E
ε
, provided the object is being
strained elastically.
Modern strain gauges use the same principal, but are made of thin metal foil instead of wire.
The foil is embedded in a pad that is easy to glue to the part being tested.
The longer the conductor, the more sensitive the gauge. With a foil strain gauge, the conductor
loops back on itself many times. The total wire length is the loop length times twice the
number of loops; in this cartoon, the total length is 14 times the loop length.
Consider the short block in Chapter 12, Example #4. A
point load is offset from both neutral axes. The total
stress at the four corners is -3.75 psi, -41.25 psi, +16.25
psi, and -21.25 psi.
In plan view, point C has a tensile stress, while points A,
B, and D have compressive stresses.
We can calculate the stress at any point along the edges
by interpolating from the corner stresses, because the
stress varies linearly from one corner to the next.
Likewise we can calculate the stresses within the area of
the block by interpolating from the edge stresses.
130
loop length
A
4 ft.
B
C
D
Plan view
2.5 ft.
σ
A
= -3.75 psi σ
B
= -41.25 psi
σ
C
= +16.25 psi
σ
D
= -21.25 psi
Point load
location
12 kips
W
x x
y
y
1.5 ft.
A
B
D
C
4 ft.
3 ft.
2.5 ft.
0.5 ft.

Chapter 15: Visualizing Stress and Strain
One way to visualize these stresses is with a grid pattern
in plan view, identifying the stress at each location, or
node. In the diagram, the nodes are at half-foot intervals.
Alternatively, we can calculate contour lines of stress
(a.k.a. isostress lines), coloring the spaces between the
lines. The pattern shows that the pink areas are in tension,
while the blue areas are in compression. The picture helps
us see that the isostress lines are diagonals, and there is a
zero stress line stretching from the AC edge to the CD
edge.
'/
/
Take a tensile bar, cut it in half transversely to the axis,
and glue the bar back together. If you pull on the bar
along the x-axis, a normal stress
σ
x
=
P
A
develops in the
adhesive. Area A is the cut surface area of the bar (the
cross-sectional area). There is no shear stress, because the
adhesive is not loaded in shear. Consider a little square
piece of adhesive: it has a normal stress σ
x
acting on the
left and right faces, but no normal stress on the top or
bottom faces, and no shear stresses.
131
A
B
C D
+16.25
+7.56
-3.75
-21.25
-41.25
+2.88
-1.81 -6.50 -11.19
-15.88 -20.56 -25.25+12.25
+3.56 -1.13 -5.81 -10.50 -15.19 -19.88 -24.56 -29.25+8.25
-0.44
-5.13
-9.81
-14.50
-19.19
-23.88 -28.56 -33.25+4.25
-4.44
-9.13
-13.81
-18.50
-23.19
-27.88 -32.56 -37.25+0.25
-8.44 -13.13 -17.81 -22.50 -27.19 -31.88
-36.56
+11.56
+6.88
+2.19 -2.50 -7.19
-11.88 -16.56
A B
C
D
0 psi
-5
-10
-15
-20
-25
-30
5
10
-35
-40
15
P
σ
x
y
x
cut

Chapter 15: Visualizing Stress and Strain
Cut a similar tensile bar in half along its x-axis, and glue
the bar back together. If you load the bar as shown, a
shear stress
τ=
P
A
develops in the adhesive. Again, area
A is the cut surface area of the bar. There is no normal
stress, because the adhesive is only loaded in shear. A
little square piece of adhesive has a shear stress acting on
the top and bottom faces, in the x direction. The square
becomes a parallelogram as it distorts.
We could call this shear stress τ
x
, because it acts along the
x direction. Think about how the little square of adhesive
distorts relative to other little squares of adhesive on its
left and right: its neighbors try to prevent the piece from
parallelogramming, so there are shear stresses in the y
direction too. The stress required to produce the
parallelogram is the same along each edge, so
τ
x
=τ
y
;
we'll use a single term
τ
xy
=τ
x
=τ
y
. A positive shear
stress is one that distorts the square clockwise relative to
its base; a negative shear stress distorts the square
counterclockwise.
Cut another bar at an angle to the axis, and glue it back
together. If you pull on the bar, the adhesive is loaded in
normal tension and in shear. The two segments of the bar
want to pull away from each other and slide along each
other. Let's define two new axes, x' and y', perpendicular
and parallel to the cut surface. We have a shear stress τ
acting parallel to the cut surface, and a tensile stress σ
x'
acting perpendicular to the cut surface, in the x' direction.
We don't have to actually cut the bar and use an adhesive;
instead, we can imagine the stresses that act in various
directions within the material. Draw a square that
represents the piece of adhesive, and rotate it in different
directions. We can calculate the stresses in the x' and y'
directions by using equations from Statics: sum of the
forces in any particular direction equals zero.
132
P
τ
y
x
cut
τ
x
τ
x
τ
y
τ
xy
τ
xy
Negative
shear stress
Positive
shear stress
y
x
cut
P
τ
x'y'
σ
x'
y'
x'
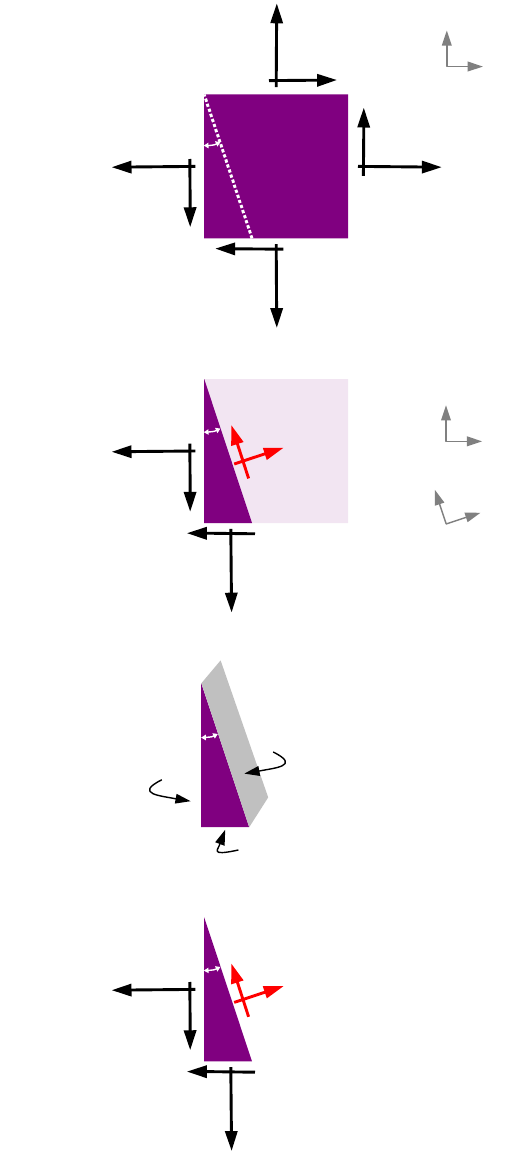
Chapter 15: Visualizing Stress and Strain
First, draw the square element. In the general case, there
could be a vertical normal stress σ
y
, so include this stress
in the sketch.
Next, cut the square along a diagonal in the y' direction,
so the normal stress acting on this surface is σ
x'
and the
shear stress acting on this surface is τ
x'y'
. The new x'-y'
coordinate axes are tilted at angle θ counterclockwise
from the original x-y coordinate axes.
The square has a depth (the thickness of the stressed
part), so each edge is actually an area in three
dimensions. Let the area of the cut surface be area a.
Using trigonometry, the area of the left surface is
a cos θ
and the area of the bottom surface is
asin θ
.
The force acting on each face is equal to the stress times
the area. We have 6 forces acting on the triangular body.
133
y
x
cut
σ
x
σ
x
σ
y
σ
y
τ
xy
τ
xy
τ
xy
τ
xy
θ
y
x
τ
x'y'
σ
x
y'
x'
σ
x'
σ
y
τ
xy
τ
xy
θ
τ
x'y
a
σ
x'
a
σ
y
a sinθ
τ
xy
a cosθ
τ
xy
a sinθ
θ
σ
x
a cosθ
θ
Area a sinθ
Area a cosθ
Area a

Chapter 15: Visualizing Stress and Strain
Look at the components of the forces acting in the x'
direction. If you add them up, the sum is zero.
σ
x '
a=σ
x
acos
2
θ+σ
y
asin
2
θ+2 τ
xy
a cos θsin θ
Notice that area a cancels, so we can write
σ
x '
=σ
x
cos
2
θ+σ
y
sin
2
θ+2 τ
xy
cos θsin θ
There are some trig identities that will help simplify the
equation into something useful:
cos
2
θ=
1+cos 2 θ
2
,
sin
2
θ=
1−cos 2θ
2
,
sin 2θ=2 cosθ sin θ
, and
cos 2θ=cos
2
θ−sin
2
θ
.
Now we get
σ
x'
=σ
x
1+cos 2θ
2
+σ
y
1−cos 2 θ
2
+τ
xy
sin 2θ
=
σ
x
+σ
x
cos 2 θ+σ
y
+σ
y
cos 2θ
2
+τ
xy
sin 2θ
=
σ
x
+σ
y
2
+
σ
x
−σ
y
2
cos 2θ+ τ
xy
sin 2θ
Following the same procedure, we can calculate the sum
of the forces in the y' direction.
τ
x' y '
a=−σ
x
a cos θsin θ+σ
y
a sinθ cos θ
−τ
xy
asin
2
θ+τ
xy
a cos
2
θ
Area a cancels. Using the trig identities, we can simplify
the equation:
τ
x ' y '
=(−σ
x
+σ
y
)cos θsin θ+τ
xy
(cos
2
θ−sin
2
θ)
=−(σ
x
−σ
y
)
sin 2 θ
2
+τ
xy
cos 2θ
=
−(σ
x
−σ
y
)
2
sin 2θ+τ
xy
cos 2θ
We can calculate the stress in the y' direction by taking
angle
θ+90°
. Using free-body diagrams and trig
identities, we get:
σ
y '
=
σ
x
+σ
y
2
−
σ
x
−σ
y
2
cos 2θ−τ
xy
sin 2θ
134
τ
x'y
a
σ
x'
a
σ
y
a sinθ sinθ
τ
xy
a cosθ sinθ
τ
xy
a sinθ cosθ
θ
σ
x
a cosθ cosθ
τ
x'y
a
σ
x'
a
σ
y
a sinθ cosθ
τ
xy
a cosθ cosθ
τ
xy
a sinθ sinθ
θ
σ
x
a cosθ sinθ
y
x
τ
x'y'
σ
x
y'
x'
σ
y'
σ
y
τ
xy
τ
xy
θ+90°

Chapter 15: Visualizing Stress and Strain
Now we have three equations that are functions of σ
x
, σ
y
,
and τ
xy
, and θ. Let's pick values of normal and shear
stresses, and see how σ
x'
, σ
y'
, and τ
x'y'
vary by plotting
stress vs. angle θ. The graph at the right shows σ
x'
as a
function of angle θ if we pick
σ
x
=1 ksi
,
σ
y
=0.5 ksi
,
and
τ
xy
=1.2 ksi
. The graph is a sine wave, with peaks,
valleys, and zero values. Picking different values of σ
x
,
σ
y
, and τ
xy
will change the amplitude and vertical position
of the sine wave, but not the period.
Notice that the maximum values of σ
x'
occur at
θ=40 °
and 220°, the minimum values occur at
θ=130 °
and
310°, and
σ
x'
=0
at
θ=100°
, 155°, 283°, and 385°.
This graph shows σ
y'
as a function of angle θ for the same
set of σ
x
, σ
y
, and τ
xy
.
The maximum values of σ
y'
occur at
θ=130°
and 310°,
the minimum values occur at
θ=40 °
and 220°, and
σ
y '
=0
at
θ=13°
, 65°, 193°, and 235°.
This graph of σ
y'
is shifted 90° to the right of the graph of
σ
x'
; as a result, you can find the angles for the maximum
values of σ
y'
by adding 90° to the angles for the maximum
values of σ
x'
.
This graph shows τ
x'y'
as a function of angle θ for the
same set of σ
x
, σ
y
, and τ
xy
.
The maximum values of τ
x'y'
occur at
θ=175°
and 355°,
shifted 45° from the maximum values of σ
x
. The
minimum values of τ
x'y'
occur at
θ=85°
and 265°, and
τ
x ' y '
=0
at
θ=39°
, 129°, 219°, and 309°.
We can see how the three stresses interrelate by plotting
them together. There are normal stresses for which the
shear stress is zero, and there are shear stresses for which
the normal stress is zero. The values and angles depend
on the input conditions (σ
x
, σ
y
, and τ
xy
).
Let's take another look at the equations for σ
x'
and τ
x'y'
:
σ
x '
=
σ
x
+σ
y
2
+
σ
x
−σ
y
2
cos 2 θ+τ
xy
sin 2θ
τ
x ' y '
=
−(σ
x
−σ
y
)
2
sin 2 θ+τ
xy
cos 2θ
Rewrite the σ
x'
equation, putting two terms on the left:
σ
x '
−
σ
x
+σ
y
2
=
σ
x
−σ
y
2
cos 2 θ+τ
xy
sin 2θ
135
Stress
(ksi)
2.0
1.0
0.0
-1.0
-2.0
0 120 180 240 300 36060
Angle θ (degrees)
σ
x'
Stress
(ksi)
2.0
1.0
0.0
-1.0
-2.0
0 120 180 240 300 36060
Angle θ (degrees)
σ
y'
Stress
(ksi)
2.0
1.0
0.0
-1.0
-2.0
0 120 180 240 300 36060
Angle θ (degrees)
τ
x'y'
Stress
(ksi)
2.0
1.0
0.0
-1.0
-2.0
0 120 180 240 300 36060
Angle θ (degrees)
τ
x'y'
σ
y'
σ
x'

Chapter 15: Visualizing Stress and Strain
Square both sides of the σ
x'
and τ
x'y'
equations:
(
σ
x '
−
σ
x
+σ
y
2
)
2
=
(
σ
x
−σ
y
2
)
2
cos
2
2θ+(σ
x
−σ
y
)τ
xy
sin 2θ cos 2θ+τ
xy
2
sin
2
2θ
τ
x ' y '
2
=
(
σ
x
−σ
y
2
)
2
sin
2
2θ−(σ
x
−σ
y
) τ
xy
sin 2 θcos 2θ+τ
xy
2
cos
2
2θ
Next, add these two equations together:
(
σ
x '
−
σ
x
+σ
y
2
)
2
+τ
x' y'
2
=
(
σ
x
−σ
y
2
)
2
cos
2
2θ+(σ
x
−σ
y
)τ
xy
sin 2 θcos 2θ+τ
xy
2
sin
2
2 θ
+
(
σ
x
−σ
y
2
)
2
sin
2
2θ−(σ
x
−σ
y
)τ
xy
sin 2θ cos2 θ+ τ
xy
2
cos
2
2θ
We can eliminate two terms because
(σ
x
−σ
y
)τ
xy
sin 2 θcos 2 θ−(σ
x
−σ
y
)τ
xy
sin 2θ cos 2θ=0
. Rewriting the equation, we
have:
(
σ
x '
−
σ
x
+σ
y
2
)
2
+τ
x' y'
2
=
(
σ
x
−σ
y
2
)
2
(cos
2
2θ+sin
2
2θ)+τ
xy
2
(sin
2
2θ+cos
2
2θ)
Using the trig identity
cos
2
2θ+sin
2
2 θ=1
, the equation simplifies to
(
σ
x '
−
σ
x
+σ
y
2
)
2
+τ
x' y'
2
=
(
σ
x
−σ
y
2
)
2
+τ
xy
2
.
The term
σ
x
+σ
y
2
is an average of two stress values, so let's call it σ
avg
. Now the equation is even simpler:
(σ
x '
−σ
avg
)
2
+τ
x ' y '
2
=
(
σ
x
−σ
y
2
)
2
+τ
xy
2
. If we define the right side of the equation as
R=
√
(
σ
x
−σ
y
2
)
2
+τ
xy
2
then
(σ
x '
−σ
avg
)
2
+τ
x ' y '
2
=R
2
. This is the equation of a circle with a radius R and a center at coordinates
(σ
avg
,0)
. In 1880, Otto
Mohr developed this method for visualizing stresses in two-dimensional and three-dimensional objects. His graphical
method is also used for diagramming strains. We can use Mohr's Circle to determine the value and direction of maximum
stresses within a loaded part.
Follow this 6-step process for drawing Mohr's circle for the stresses acting at a point within a stressed object. For best
results, use a compass and straightedge on graph paper.
In this example, use the same stresses as before:
σ
x
=1 ksi
,
σ
y
=0.5 ksi
, and
τ
xy
=1.2 ksi
.
% Draw two axes. Label the horizontal axis σ and the
vertical axis τ.
136
τ
σ

Chapter 15: Visualizing Stress and Strain
- Mark the center of the circle at coordinates
(σ
avg
,0)
and label it for center. In this case,
σ
avg
=
σ
x
+σ
y
2
=
1ksi+0.5 ksi
2
=0.75ksi
.
. Mark point
(σ
x
,−τ
xy
)
on the graph; in this case,
(1ksi ,−1.2 ksi)
. Label this point *.
2 Placing your compass point at the center of the
circle, draw a circle passing through this point. The radius
of Mohr's circle is:
R=
√
(
σ
x
−σ
y
2
)
2
+τ
xy
2
=
√
(
1 ksi−0.5 ksi
2
)
2
+(1.2 ksi)
2
=1.226 ksi
Notice the circle also passes through point
(σ
y
, τ
xy
)
,
which is
(0.5 ksi ,1.2 ksi)
. Mark this point and label it .
A line passing through points * and is the diameter of
Mohr's circle.
4 The maximum normal stress occurs at point ; we
call it σ
1
. The minimum normal stress occurs at point ;
we call it σ
2
. The maximum shear stress occurs at point +;
we call this τ
max
.These three stresses are called Principal
Stresses.
You can measure these values off the graph, or you can
calculate them:
σ
1
=σ
avg
+R=0.75ksi+1.226 ksi=1.976 ksi
σ
2
=σ
avg
−R=0.75 ksi−1.226 ksi=−0.476 ksi
τ
max
=R=1.226 ksi
137
τ
σ
τ
σ
(σ
x
, -τ
xy
)
τ
σ
(σ
x
, -τ
xy
)
R
(σ
y
, τ
xy
)
.
τ
σ
(σ
x
, -τ
xy
)
σ
1
R
τ
max
σ
2
(σ
y
, τ
xy
)
.
7
-

Chapter 15: Visualizing Stress and Strain
9 Starting on line segment *-, measure the angle
counterclockwise about point to line segment - . This
angle is 2θ.
tan 2θ=
τ
xy
(σ
x
−σ
y
)/2
=
2τ
xy
σ
x
−σ
y
=
2(1.2 ksi)
1ksi−0.5 ksi
=4.8
2θ=tan
−1
4.8=78.2°
θ=
78.2°
2
=39.1°
This is the angle of the principal stress σ
1
. The angle of
principal stress σ
2
is
θ=90°+39.1° =129.1°
.
Going back to the original stress element, we had
σ
x
=1 ksi
,
σ
y
=0.5 ksi
, and
τ
xy
=1.2 ksi
. If we rotate
the element counterclockwise 39.1°, in this orientation
there are no shear stresses, and the principal stresses are
σ
1
=1.976 ksi
tension and
σ
2
=−0.476 ksi
compression. The maximum shear stress
τ
max
=1.226 ksi
is oriented 45° from the maximum normal stress, at
θ=45° +39.1 °=84.1°
.
,8
σ
x
Applied normal stress in the x direction, which could be from tension or compression (P/A), bending (Mc/I
or M/Z), hoop stress (p d
i
/2t), longitudinal stress (p d
i
/4t), etc.
σ
y
Applied normal stress in the y direction, which could be from tension or compression (P/A), bending (Mc/I
or M/Z), hoop stress (p d
i
/2t), longitudinal stress (p d
i
/4t), etc.
τ
xy
Applied shear stress. Could be from bending (VQ/It), torsion (Tc/J), applied shear load (P/A), etc.
R Radius of Mohr's circle, equal to maximum shear stress τ
max
and calculated as
R=
√
(
σ
x
−σ
y
2
)
2
+τ
xy
2
Point * Point on Mohr's circle, plotted as (σ
x
, -τ
xy
)
Point Point on Mohr's circle, plotted as (σ
y
, +τ
xy
)
Point Point on Mohr's circle, plotted as (σ
avg
, 0) where
σ
avg
=(σ
x
+σ
y
)/ 2
Point Principal stress σ
1
which is the maximum normal stress, calculated as
σ
1
=σ
avg
+R
Point Principal stress σ
2
which is the minimum normal stress, calculated as
σ
2
=σ
avg
−R
θ
Angle at which the principal stresses act. All angles on Mohr's circle axes are double angles. Calculate as
tan 2θ=
τ
xy
(σ
x
−σ
y
)/2
. One common mistake is to enter τ
max
in place of τ
xy
.
x', y' Axes along which the principal stresses act.
138
τ
σ
(σ
x
, -τ
xy
)
σ
1
R
τ
max
2θ
σ
2
(σ
y
, τ
xy
)
.
7
-
2θ
-τ
xy
(
σ
x
−σ
y
2
)
σ
x
−σ
y
.
y
x
σ
x
=1 ksi
τ
xy
=1.2 ksi
σ
y
=0.5 ksi
y'
σ
2
= -0.476 ksi
σ
1
=1.976 ksi
x'
θ
= 39.1°

Chapter 15: Visualizing Stress and Strain
!"
A brass rod with a diameter of 0.5 inches is pulled with a load of 2000 lb. as shown. Calculate the
applied stresses σ
x
, σ
y
, and τ
xy
. Use Mohr's circle to find the principal stresses σ
1
and σ
2
, angle θ, and
the maximum shear stress τ
max
at point *.
The applied normal stress is in the y direction; there is no applied shear stress.
σ
x
=0
σ
y
=
P
A
=
4 P
π d
2
=
4⋅2000 lb.
π(0.5in.)
2
∣
kip
10
3
lb.
=10.2 ksi
τ
xy
=0
σ
avg
=
σ
x
+σ
y
2
=
0 ksi+10.2 ksi
2
=5.09 ksi
R=
√
(
σ
x
−σ
y
2
)
2
+ τ
xy
2
=
√
(
0 ksi −10.2 ksi
2
)
2
+(0 ksi)
2
= 5.09 ksi
σ
1
=σ
avg
+R=5.09 ksi+5.09 ksi=10.2 ksi
σ
2
=σ
avg
−R=5.09 ksi−5.09 ksi=0 ksi
τ
max
=R=5.09ksi
Angle
θ=0
, by inspection, confirming that the maximum normal
stress (principal stress #1) is the normal stress in the y direction.
Rotate line segment - about point to create line segment -+ 90° to
the principal stress direction. Since all angles in Mohr's circle are
double angles, we see that the maximum shear stress acts 45° to the
principal stresses.
This photograph of a broken tensile specimen proves the existence of
the maximum shear stress acting 45° to the axis of the rod. The
specimen is pulled beyond its yield strength. Internally, microscopic
voids form in a plane perpendicular to the axis; these voids coalesce to
form a crack that grows from the center towards the surface of the rod.
At some point, there is not enough material to support the load, and the
rod shears at 45°, creating the classic cup-and-cone fracture surface of
a ductile tensile specimen.
139
P
y
x
τ
σ
(σ
x
, -τ
xy
)
σ
1
τ
max
= 5.1 ksi
σ
2
(σ
y
, τ
xy
)
.
-
(10.2 ksi, 0)(0, 0)
(σ
avg
, 0)
(5.1 ksi, 0)
τ
σ
(σ
x
, -τ
xy
)
σ
1
τ
max
= 5.1 ksi
σ
2
(σ
y
, τ
xy
)
.
-
(10.2 ksi, 0)
(0, 0)
(σ
avg
, 0)
(5.1 ksi, 0)
90°

Chapter 15: Visualizing Stress and Strain
!#
The rod in Example #1 is pulled as before, and also twisted with a torque of 45 ft.⋅lb.
Once again the applied normal stress is in the y direction, but the torque creates an applied shear
stress.
σ
x
=0
σ
y
=
P
A
=
4 P
π d
2
=
4⋅2000 lb.
π(0.5in.)
2
∣
kip
10
3
lb.
=10.2 ksi
as before
τ
xy
=
T c
J
where
c=
d
2
and
J =
π d
4
32
(see Chapter 7 – torsion in a round shaft produces a shear
stress at the surface)
Substituting,
τ
xy
=
T d
2
32
π d
4
=
16 T
π d
3
=
16 45ft⋅lb.
π(0.5 in.)
3
∣
12in.
ft.
∣
kip
10
3
lb.
=22.0 ksi
σ
avg
=
σ
x
+σ
y
2
=
0 ksi+10.2 ksi
2
=5.09 ksi
R=
√
(
σ
x
−σ
y
2
)
2
+ τ
xy
2
=
√
(
0 ksi −10.2 ksi
2
)
2
+(22.0 ksi)
2
= 22.6 ksi
σ
1
=σ
avg
+R=5.09 ksi+22.6 ksi=27.1 ksi
σ
2
=σ
avg
−R=5.09 ksi−22.6 ksi=−16.9ksi
τ
max
=R=22.6 ksi
tan 2θ=
2τ
xy
σ
x
−σ
y
=
2(22.0ksi )
0ksi−10.2 ksi
=−4.32
2θ=tan
−1
−4.32=−77.0°
θ=
−77.0 °
2
=−38.5°
;
−38.5° +90 °=51.5°
We can also use Mohr's circle to find out the stress in a plane at any angle α. Rotate counterclockwise through angle 2α
from line segment *- to a new line segment */- to find the shear and normal stresses acting in this direction.
140
P
T
y
x
τ
σ
(σ
x
, -τ
xy
)
σ
1
=27.1 ksi
R
τ
max
=22.6 ksi
2θ
σ
2
(σ
y
, τ
xy
)
.
7
-
(10.2 ksi, 22.0 ksi)
(0 ksi, -22.0 ksi)
-16.9 ksi
-77°

Chapter 15: Visualizing Stress and Strain
!$
A 20" diameter cylindrical tank with a ¼" wall thickness is
pressurized to 700 psi. If the barrel of the tank is made
from a strip of steel welded in a spiral at 65°, what are the
normal and shear stresses acting on the weld?
From Chapter 4,
σ
x
=σ
long
=
p d
i
4t
=
700 psi 20in.
4 0.25 in.
∣
ksi
10
3
psi
=14 ksi
σ
y
=σ
hoop
=
p d
i
2t
=
700 psi 20 in.
2 0.25in.
∣
ksi
10
3
psi
=28 ksi
τ
xy
=0
Now solve the Mohr's circle equations.
σ
avg
=
σ
x
+σ
y
2
=
14 ksi+28 ksi
2
=21 ksi
R=
√
(
σ
x
−σ
y
2
)
2
+τ
xy
2
=
√
(
14 ksi−28 ksi
2
)
2
+(0 ksi)
2
= 7ksi
σ
1
=σ
avg
+R=21 ksi+7 ksi=28 ksi
σ
2
=σ
avg
−R=21 ksi−7 ksi=14 ksi
τ
max
=R=7ksi
Angle
θ=0
, by inspection.
Rotate counterclockwise through angle
2α=2⋅65 °=130 °
from line segment *- to a new line segment */-. The normal
stresses acting perpendicular and parallel to the weld are
σ
avg
±Rcos 2α=21 ksi±7 ksi cos(130° )=16.5 ksi & 25.5 ksi
.
The shear stress acting along the weld
R sin 2 α=7 ksi sin(130° )=5.4 ksi
.
Since the normal stress acting on the spiral weld is 91% of the maximum normal stress (the hoop stress), the weld
efficiency can be as low as 91% before the tank will fail at a weld.
If the tank were manufactured like welded pipe, with a longitudinal weld instead
of a spiral weld, then anything less than 100% weld efficiency would cause the
tank to fail at the weld instead of splitting in the base metal from excessive hoop
stress.
The end cap welds can have as little as 50% weld efficiency and still survive,
because the longitudinal stress is 50% of the hoop stress.
Chapter 9 discussed normal and shear stresses in beams. We can use Mohr's circle to look at the normal and shear stresses at
any location within a beam.
141
y
x
α = 65°
τ
σ
(σ
x
, -τ
xy
)
σ
1
τ
max
= 7 ksi
σ
2
(σ
y
, τ
xy
)
.
-
(28 ksi, 0)
(14 ksi, 0)
(σ
avg
, 0)
2α=130°
(16.5 ksi, 5.4 ksi)
8
R
(21 ksi, 0)
.8
(25.5 ksi, -5.4 ksi)

Chapter 15: Visualizing Stress and Strain
!%
A 4 cm × 12 cm titanium bar is loaded as a beam and as a
compression member. Find the stresses in the bar 1 cm
above the neutral axis, at the midspan.
First, determine whether the bar will fail in buckling. From
Chapter 14,
P
cr
=
π
2
E I
L
2
.
If the load is greater than P
cr
, then the bar fails in buckling. The moment of inertia about the weak axis is
I =
12 cm(4 cm)
3
12
=64 cm
4
, therefore
P
cr
=
π
2
114 GPa 64 cm
4
(3 m)
2
∣
10
6
kN
GPa m
2
∣
m
4
(100 cm)
4
=80 kN
. Since the applied axial load
is less than 80 kN, the bar does not buckle.
The axial stress in the bar is
σ
xaxial
=
P
A
=
−25 kN
4cm⋅12 cm
∣
MPa m
2
10
3
kN
∣
(100cm)
2
m
2
=−5.2 MPa
The bending stress in the bar at the top or bottom surface is
σ
x bending
=
M c
I
, but we need the bending stress at a location 1 cm
above the neutral axis, so
σ
x bending
=
M y
I
where
y=1 cm
. The
beam is being bent in the strong direction, so
I =
4 cm (12cm)
3
12
=576 cm
4
σ
xbending
=
7.5 kN⋅m 1 cm
576cm
4
∣
MPa m
2
10
3
kN
∣
(100cm)
3
m
3
=13.0MPa
Add the axial and bending stresses together to find the total stress in
the x direction.
σ
x total
=σ
x axial
+σ
x bending
=−5.2 MPa+13.0 MPa=7.8 MPa
σ
y
=0
Shear stress in the beam is
τ
xy
=
V Q
I t
where
Q= A ' y=(4 cm×5 cm )3.5 cm=70 cm
3
τ
xy
=
5kN 70cm
3
576cm
4
4cm
∣
MPa m
2
10
3
kN
∣
(100 cm)
2
m
2
=1.5 MPa
142
A B
R
A
3 m
R
B
10 kN
25 kN
4 cm
12
cm
A B
R
A
= 5 kN
V
1
=5 kN
V
V
2
= -5 kN
3 m
M
max
= 7.5 kN⋅m
M
R
B
= 5 kN
10 kN
Bending load only
A B
Axial load only
25 kN
A'=20 cm
2
4 cm
12
cm
y=3.5 cm
1 cm

Chapter 15: Visualizing Stress and Strain
!%
Now solve the Mohr's circle equations.
σ
avg
=
σ
x
+σ
y
2
=
7.8 MPa+0 MPa
2
=3.9 MPa
R=
√
(
σ
x
−σ
y
2
)
2
+τ
xy
2
=
√
(
7.8 MPa−0MPa
2
)
2
+(1.5 MPa)
2
= 4.2 MPa
σ
1
=σ
avg
+R=3.9 MPa+4.2 MPa=8.1 MPa
σ
2
=σ
avg
−R=3.9 MPa−4.2 MPa =−0.2 MPa
τ
max
=R=4.2 MPa
tan 2θ=
2 τ
xy
σ
x
−σ
y
=
2(1.5 MPa)
7.8 MPa−0
=0.385
2θ=tan
−1
(0.385)=21.0°
θ=
21.0°
2
=10.5° ; 10.5°+90 °=100.5 °
!&
A 6 ft. long, 3 in. diameter thin-walled hollow tube has a wall thickness of
0.060 in. The tube is loaded in tension, torsion and bending, as shown, and it is
pressurized to 450 psi.
P
x
=600 lb.
,
P
y
=150 lb.
and
T =75 ft.⋅lb.
. Points %
and - are on the surface of the tube at the midspan (3 ft. from the wall), with
point % at the neutral axis and point - at the top.
The x direction is horizontal along the axis of the pipe, the y direction is
vertical, and the z direction is horizontal and transverse to the axis of the pipe.
Calculate the normal and shear stresses due to the applied loads, then
add up the terms. Horizontal applied load P
x
creates a tensile stress
σ
x
=P
x
/A
at points % and -. Vertical applied load P
y
creates a a shear stress
τ
xy
=VQ / It
at point % and a bending stress
σ
x
=Mc/ I
at point -. Torque T creates a shear
stress
τ
xy
=Tc / J
at point % and a shear stress
τ
xz
=Tc /J
at point -. Pressure
p creates a hoop stress
σ
y
= p d
i
/2t
at point %, a hoop stress
σ
z
= p d
i
/2t
at
point -, and a longitudinal stress
σ
x
= p d
i
/4 t
at points % and -.
After combining the σ
x
terms, the σ
y
terms, the σ
z
terms, the τ
xy
terms, and the τ
xz
terms. Draw Mohr's circle at for % using
σ
x
, σ
y
, and τ
xy
. Draw Mohr's circle for point - using σ
x
, σ
z
, and τ
xz
.
143
τ
σ
(σ
x
, -τ
xy
)
σ
1
R
τ
max
=4.2 MPa
2θ = 21°
σ
2
(σ
y
, τ
xy
)
.
7
-
-0.2 MPa
8.1 MPa
(0, 1.5 MPa)
(7.8 MPa,
1.5 MPa)
3.9 MPa
P
y
T
P
x
%
-
-
%
y
x
z
Cross-section
y
z

Chapter 15: Visualizing Stress and Strain
!&
First, calculate quantities that will be needed in multiple equations.
Inside diameter
d
i
=d
o
−2 t=3in.−2×0.060 in.=2.88 in.
Dimension
c=
d
o
2
=
3in.
2
=1.5 in.
Cross-sectional area
A=
π
4
[
d
o
2
−d
i
2
]
=
π
4
[
(3 in.)
2
−(2.88 in.)
2
]
=0.5542 in.
2
Moment of inertia about the x-x axis
I
x
=
π
64
[
d
o
4
−d
i
4
]
=
π
64
[
(3 in.)
4
−(2.88 in.)
4
]
=0.5990 in.
4
Polar moment of inertia about the x-x axis
I
x
=
π
32
[
d
o
4
−d
i
4
]
=
π
64
[
(3 in.)
4
−( 2.88in.)
4
]
=0.2995 in.
4
1
At points % and -,
σ
x1
=σ
x2
=
P
x
A
=
600 lb.
0.5542 in.
2
=1,083 psi
There is no bending stress at point % because it is at the neutral axis.
To calculate the bending stress at point -, we need the bending
moment at the midspan of a cantilever beam due to a point load at the
free end. Use the Formula Method to find
M
x =3ft.
=P
y
x=150lb.×3 ft.=450 ft.lb.
Bending stress
σ
x2
=
M c
I
=
450ft.lb. 1.5in.
0.5990 in.
4
∣
12 in.
ft.
=13,520 psi
Vertical load P
y
creates a VQ/It shear stress due to bending at point %
but not at point -, where shear stress due to bending is zero.
Point % is at the neutral axis, so A' is the cross-sectional area of a half
pipe:
A' =
π
8
[
d
o
2
−d
i
2
]
=
π
8
[
(3 in.)
2
−(2.88 in.)
2
]
=0.2271in.
2
The distance from the neutral axis to the center of gravity of a half pipe is
̄
y=
2
[
d
o
3
−d
i
3
]
3π
[
d
o
2
−d
i
2
]
=
2
[
(3in. )
3
−(2.88 in.)
3
]
3 π
[
3in.
2
−(2.88 in.)
2
]
=0.9360 in.
Q= A '
̄
y=0.2271 in.
2
×0.9360 in.=0.2593 in.
3
, so
τ
xy1
=
V Q
I t
=
150 lb. 0.2593in.
3
0.5990 in.
4
3 in.
=21.65 psi
Torque produces the same value of shear stress at points % and -.
τ
xy1
=τ
xz2
=
T c
J
=
75 ft.lb. 3 in.
0.2995in.
4
∣
12 in.
ft.
=9,015 psi
144
A B
R
By
150 lb.
Bending load only
A B
Axial load only
600 lb.
R
Bx
M
B
x = 3 ft.
V
-150 lb.
M
max
= -900 ft.⋅lb.
M
M
x=3 ft.
= -450 ft.⋅lb.
d
o
y
d
i
A'

Chapter 15: Visualizing Stress and Strain
!&
At both points, longitudinal stress
σ
x1
=σ
x2
=
p d
i
4t
=
450 lb.
in.
2
3 in.
4 0.060 in.
=5,625 psi
At both points, hoop stress
σ
y1
=σ
z2
=
p d
i
2t
=
450 lb.
in.
2
3 in.
4 0.060 in.
=11,250 psi
'/%
σ
x1
=1,083 psi+5,625 psi=6,708 psi
σ
y1
=11,250 psi
τ
xy1
=9,015 psi+22 psi=9,037 psi
σ
avg1
=
σ
x1
+σ
y1
2
=
6,708 psi+11,250 psi
2
=8,979 psi
R=
√
(
σ
x1
−σ
y1
2
)
2
+τ
xy1
2
=
√
(
6,708 psi−11,250 psi
2
)
2
+(9,037 psi)
2
=9,318 psi
σ
P1# 1
=σ
avg1
+R=18,297 psi
σ
P1# 2
=σ
avg1
−R=−339 psi
tan 2θ=
2 τ
xy
σ
x
−σ
y
=
2(9,037 psi)
6,708 psi−11,250 psi
=−3.98
2θ=tan
−1
−3.98=−76°
,
θ=
−76.0°
2
=−38 °
,
−38 °+90° =52 °
'/-
σ
x2
=1,083 psi+13,520 psi+5,625 psi=20,228 psi
σ
z2
=11,250 psi
τ
xy2
=9,015 psi
σ
avg2
=
σ
x2
+σ
y2
2
=
20,228 psi+11,250 psi
2
=15,740 psi
R=
√
(
σ
x2
−σ
z2
2
)
2
+τ
xz2
2
=
√
(
20,228 psi−11,250 psi
2
)
2
+(9,015 psi)
2
=10,070 psi
σ
P2# 1
=σ
avg2
+R=25,810 psi
σ
P2# 2
=σ
avg2
−R=5,670 psi
tan 2θ=
2 τ
xy
σ
x
−σ
z
=
2(9,015 psi)
20,228 psi−11,250 psi
=2.01
2θ=tan
−1
2.01=64 °
,
θ=
64 °
2
=32°
,
32 °+90 °=122 °
-
Design engineers don't prevent failure, they manage it by designing products and structures so that when they fail due to old
age, abuse, or ordinary service, nobody is injured. How do we define failure? It depends on the product or structure. A
bridge deck could be described as a failure if it deflects too far, even though it does not break. A shear pin in a snowblower
145
τ
σ
(σ
x
, -τ
xy
)
σ
1
R
τ
max
= 9318 psi
2θ = -76°
σ
2
(σ
y
, τ
xy
)
.
7
-
-339 psi
(11250, 9037 psi)
(6708, -9037 psi)
18297 psi
τ
σ
(σ
x
, -τ
xz
)
σ
1
R
τ
max
= 10070 psi
2θ = 64°
σ
2
(σ
z
, τ
xz
)
.
7
-
(20228, -9015 psi)
5670 psi
25810 psi
(11250, 9015 psi)

Chapter 15: Visualizing Stress and Strain
fails if it does not break when the blades are overloaded by ice, or does break under ordinary snow load.
In Strength of Materials, elastic formulas do not work in the plastic zone, and usually we do not want plastic deformation
during service, therefore we can define failure as yielding for most products or structures.
William Rankine, a 19
th
century Scottish engineer,
developed the Maximum Normal Stress Theory. He
considered materials having the same strength in tension
and compression (such as steel, not cast iron). He
proposed a failure stress criterion
σ
f
=σ
P max
where σ
f
is
the failure stress and σ
Pmax
is the maximum principal
stress. If we plot principal stresses σ
1
and σ
2
on x and y
coordinates, the part is “safe” if the combined stress point
is within the square.
Charles-Augustin de Coulomb, a 19
th
century French
physicist, and Henri Tresca, a 19
th
century French
engineer, developed the Maximum Shear Stress Theory
(also known as the Tresca Theory), which defines failure
as
τ
f
=τ
max
=
σ
max
−σ
min
2
. This theory is more
conservative than the Maximum Normal Stress Theory, as
it cuts off the upper left and lower right corners of the
square “safe” zone.
In metals, we have a linear elastic curve on the stress-
strain diagram. The area under the curve equals the strain
energy per unit volume,
u=
σ ε
2
. Richard Edler von
Mises was a Jewish mathematician who escaped Austria
when the Nazis rose to power, and later joined the faculty
at Harvard. He developed the most widely-used failure
criterion. From the energy per unit volume equation, he
derived:
σ
f
=
√
σ
1
2
−σ
1
σ
2
+σ
2
2
where σ
1
and σ
2
are the
principal stresses. The von Mises or Maximum Distortion
Energy Theory produces an elliptical “safe zone”.
Notice on all three stress graphs, the “safe” envelopes all
pass through the same four points on the two axes,
marked in red.
A number of other failure theories apply to special cases, such as the Maximum Strain Theory of Barré de Saint-Venant, and
the Internal Friction Theory. However, von Mises is used widely in finite element programs because it fits more data than
other methods.
+,
The average normal stress (center of Mohr's circle) is
σ
avg
=
σ
x
+σ
y
2
, and the radius is
R=
√
(
σ
x
−σ
y
2
)
2
+τ
xy
2
The principal stresses are
σ
1
=σ
avg
+R
and
σ
2
=σ
avg
−R
. The maximum shear stress
τ
max
=R
146
σ
1
σ
2
Safe
Not
safe
σ
f
σ
f
-σ
f
-σ
f
Not
safe
σ
2
σ
f
σ
1
Safe
σ
f
-σ
f
-σ
f
Not
safe
σ
2
σ
1
Safe
ε
σ
area=
σε
2

Chapter 15: Visualizing Stress and Strain
Find the angle of principal stresses with
tan 2θ=
[
τ
xy
(
σ
x
−σ
y
2
)
]
→ 2 θ=tan
−1
[
τ
xy
(
σ
x
−σ
y
2
)
]
→ θ=
[2θ]
2
and 90 °+
[2θ]
2
147

Bibliography
1
Sometimes when you are learning a new topic, it's helpful to look at other textbooks. The Engineering Technology
textbooks focus on algebraic and trigonometric solutions, while Engineering textbooks also use calculus. Symbols used in
these textbooks vary; authors use different symbols for force (C, F, N, P, Q, T), normal stress/strength (σ, s, f, F, S), shear
stress/strength (τ, s
s
, S
s
), Poisson's ratio (ν, μ), section modulus (S, Z), length (L, l), temperature (T, t), pressure (p, R), radius
of curvature (R, ρ), radius of gyration (r, k, q), and stress concentration (k, K, K
conc
, K
t
). Check the table of terminology
before using the equations.
The basic theory of Strength of Materials has not changed in many decades. Material properties have improved – structural
steel is better than it used to be – and some industry standards for factors of safety have changed. Newer textbooks have
full-color diagrams and online resources, including videos and animations.
George Limbrunner & Craig D'Allaird, Applied Statics and Strength of Materials, 6
th
ed., Pearson Prentice Hall, 2016.
Fa-Hwa Cheng, Statics and Strength of Materials, 2
nd
ed., Glencoe/McGraw-Hill, 1997.
Lawrence J. Wolf, Statics and Strength of Materials: A Parallel Approach to Understanding Structures, Merrill, 1988.
Ottmar W. Eckardt, Strength of Materials, Holt, Rinehart and Winston, 1969.
Alfred Jensen, Statics and Strength of Materials, McGraw-Hill, 1962.
R.C. Hibbeler, Statics and Mechanics of Materials, 3
rd
ed., Pearson Prentice Hall, 2011.
Madhukar Vable, Intermediate Mechanics of Materials, 2
nd
ed., Expanding Educational Horizons, 2013.
William Riley, Leroy Sturges, & Don Morris, Mechanics of Materials, 6
th
ed., John Wiley & Sons, 2007.
Ferdinand Beer, E. Russell Johnston, Jr., John DeWolf, & David Mazurek, Mechanics of Materials, 7
th
ed., McGraw-
Hill, 2014. Beer & Johnston pioneered the design of modern mechanics textbooks, using many examples and drawings.
Joseph Edward Shigley, Applied Mechanics of Materials, McGraw-Hill, 1976.
A0'
A textbook is usually written for a specific course. Other books that are not course-specific are still useful in engineering
practice; these include histories of technology, handbooks of design specifications, anthologies of mechanism designs, etc.
Warren Young, Richard Budynas, & Ali Sadegh, Roark's Formulas for Stress and Strain, 8
th
ed., McGraw-Hill, 2011.
Wood Handbook – 2010 Centennial Edition, General Technical Report FPL-GTR-190. Madison, WI: U.S. Department
of Agriculture, Forest Service, Forest Products Laboratory. Available online at www.fpl.fs.fed.us.
Walter Pilkey & Deborah Pilkey, Peterson's Stress Concentration Factors, 3
rd
ed., Wiley, 2008. The original edition of
1953 contains hundreds of 7"×10" hand-drawn graphs. Most of the data was developed experimentally using
photoelastic tests; some graphs are based on mathematical models. Rudolph Peterson was the manager of the Mechanics
department at Westinghouse Research Laboratories.
Eugene Avallone, Theodore Baumeister III, & Ali Sadegh, Mark's Standard Handbook for Mechanical Engineers, 11
th
ed., McGraw-Hill, 2006.
J.E. Gordon, Structures: Or Why Things Don't Fall Down, Da Capo Press, 2003
Stephen P. Timoshenko, History of Strength of Materials, Dover, 1983 (reprint from McGraw-Hill, 1953).
148

Appendix A: Units
*1*&
The SI system of units (Système International), also
commonly called the metric system, uses prefixes to
indicate scale. Learn the prefixes, and unit
conversion will become easy. For example, 1 kN is
10
3
newtons, 1 MPa is 10
6
pascals, and 1 Pa is 1
N/m
2
. If you are converting 600 kN/m
2
to MPa, you
can either convert everything to the lowest level of
meters and newtons:
600 kN
m
2
∣
10
3
N
kN
∣
MPa m
2
10
6
N
=0.6 MPa
or you can recognize that 1 MPa is 10
3
kPa and take
fewer steps:
600kN
m
2
∣
MPa m
2
10
3
kN
=0.6 MPa
Prefix Abbrev. Multiplier Literal meaning
nano- n = 10
−9
dwarf (Greek)
micro- μ = 10
−6
small (Greek)
milli- m = 10
−3
thousand (Latin)
centi- c = 10
−2
hundred (Latin)
kilo- k = 10
3
thousand (Greek)
Mega- M = 10
6
great (Greek)
Giga- G = 10
9
giant (Greek)
Tera- T = 10
12
monster (Greek)
Quantity Unit Symbol Definition
Length meter m
Mass gram g
Force or Weight newton N kg⋅m/s
2
Stress or Pressure pascal Pa N/m
2
Moment or Torque newton meter N⋅m
A very useful SI conversion factor for stress:
1MPa =1 N /mm
2
The US Customary system of units, also commonly
called the English system, generally does not use
prefixes to indicate scale; the exception is “kips” for
“kilopounds” (1000 lb.). Instead, we use conversion
factors to go from one scale to the next. Most
customary unit symbols are abbreviations with
periods: “ft.” not “ft”, “in.” not “in”; exceptions
include “psi” and “ksi” which have no periods.
In the construction trades, the term “yard” is an
abbreviation for “cubic yard”, so 3 yards of concrete
is actually 3 cubic yards, or 27 cubic feet.
Quantity Unit Symbol Definition
Length foot ft.
Mass slug S
Force or Weight pound lb.
Stress or Pressure pounds per sq. in. psi lb./in.
2
Moment or Torque foot pound ft.⋅lb.
Unit Equivalent
1 ft. = 12 in.
1 yd. = 3 ft.
1 kip = 1,000 lb.
1 ksi = 1,000 psi
1 ton = 2,000 lb.
149

Appendix B: Materials Properties
*1&'
Apply a load to a material and measure the response to obtain Mechanical Properties such as yield strength, Young's
modulus, elongation, impact resistance, and fatigue life. All other properties are called Physical Properties, including
thermal expansion, electrical conductivity, density, color, and specific heat. Some properties vary very little, while others
have large ranges. For example, Young's modulus for steels varies less than ±1½% because this property is related to bond
strength at the atomic level. The yield strength of a grade of steel can vary ±15% due to variations in composition and
processing. The weakest steels have a yield strength < 25 ksi, while the strongest have a yield strength > 300 ksi.
'@@D
."96:4;<<5
Material Specific
weight
Yield
strength
(tension)
Ultimate
strength
(tension)
Ultimate
strength
(compression)
Ultimate
strength
(shear)
Young's
modulus
Shear
modulus
Thermal
expansion
coefficient
Poisson's
ratio
γ
σ
YS
σ
UTS
σ
UCS
τ
ult
E G α ν
(lb./in.
3
) (ksi) (ksi) (ksi) (ksi) (10
6
psi) (10
6
psi) (10
-6
in./
(in.°F))
-
Steels
ASTM A36 0.284 36 58 - - 30 12 6.5 0.25
ASTM A992 (HSLA) 0.284 50 65 - - 30 12 6.5 0.25
AISI 80X (HSLA) 0.284 80 100 - - 30 11.6 6.5 0.28
AISI 1020, annealed 0.284 43 57 - - 30 12 6.8 0.25
AISI 1020, cold rolled 0.284 48 65 - - 30 12 6.8 0.25
AISI 1040, annealed 0.284 51 75 - - 30 12 6.3 0.25
AISI 1040, cold rolled 0.284 60 90 - - 30 12 6.3 0.25
AISI 4140, annealed 0.284 61 95 - - 30 12 6.8 0.25
AISI 8620, annealed 0.284 56 78 - - 30 12 6.2 0.25
Stainless steels
Type 304, annealed 0.290 30 75 - - 28 12.5 9.6 0.29
Type 304, cold rolled 0.290 110 150 - - 28 12.5 9.6 0.29
Type 409, annealed 0.280 30 55 - - 29 11.3 6.5 0.28
Cast irons
Grade 4 austempered ductile iron 0.260 155 200 - - 24.4 9.4 5.9 0.25
Class 35 gray cast iron 0.260 - 35 125 48.5 10.9 6.4 7.2 0.29
Aluminum alloys
2024-T4 0.101 47 68 - 41 10.6 4.0 12.9 0.33
6061-T6 0.098 40 45 - 30 10.0 3.8 13.1 0.33
7075-T6 0.101 73 83 - 48 10.4 3.9 13.1 0.33
Magnesium alloys
AZ80A, as extruded 0.065 36 49 - 22 6.5 2.4 14.0 0.35
AZ80A, T5 temper 0.065 40 55 - 24 6.5 2.4 14.0 0.35
Copper alloys
C10800 copper, hard drawn 0.323 32 40 - 26 17.0 6.4 9.4 0.33
C26000 cartridge brass, annealed 0.308 16 48 - 34 16.0 6.0 11.1 0.38
C26000 cartridge brass, rolled 0.308 52 70 - 42 16.0 6.0 11.1 0.38
C63000 aluminum bronze, annealed 0.274 53 111 - - 17.0 6.4 9.0 0.33
Titanium alloys
Ti-6Al-4V, annealed 0.160 120 130 - 80 16.5 6.1 4.8 0.34
Ti-6Al-4V, heat treated 0.160 160 170 - - 16.5 6.1 4.8 0.34
Concrete & Stone
Unreinforced concrete (range of
grades)
0.0868
0.1× σ
UCS
3 to 4
0.5× σ
UCS
2.5 to 4 5.5 0.1 to
0.20
Granite (typical) 0.0972 25 7.0 3.6 0.28
Limestone (typical) 0.0961 8 to 16 6.0 2.8 0.21
Sandstone (typical) 0.0903 6 2.5 5.2 0.28
150

Appendix B: Materials Properties
.#96:435
Material Density Yield
strength
(tension)
Ultimate
strength
(tension)
Ultimate
strength
(compression)
Ultimate
strength
(shear)
Young's
modulus
Shear
modulus
Thermal
expansion
coefficient
Poisson's
ratio
ρ
σ
YS
σ
UTS
σ
UCS
τ
ult
E G α ν
(g/cm
3
) (MPa) (MPa) (MPa) (MPa) (GPa) (GPa) (10
-6
mm/
(mm°C))
-
Steels
ASTM A36 7.85 250 400 - - 207 83 11.7 0.25
ASTM A992 (HSLA) 7.85 345 450 - - 207 83 11.7 0.25
AISI 80X (HSLA) 7.85 550 690 - - 207 80 11.7 0.28
AISI 1020, annealed 7.85 295 395 - - 207 83 11.7 0.25
AISI 1020, cold rolled 7.85 330 450 - - 207 83 11.7 0.25
AISI 1040, annealed 7.85 350 520 - - 207 83 11.3 0.25
AISI 1040, cold rolled 7.85 415 620 - - 207 83 11.3 0.25
AISI 4140, annealed 7.85 420 655 - - 207 83 12.3 0.25
AISI 8620, annealed 7.85 385 540 - - 207 83 11.1 0.25
Stainless steels
Type 304, annealed 8.00 205 515 - - 193 86 17.2 0.29
Type 304, cold rolled 8.00 760 1035 - - 193 86 17.2 0.29
Type 409, annealed 7.80 205 380 - - 200 78 11.7 0.28
Cast irons
Grade 4 austempered ductile iron 7.1 1100 1400 - - 168 65 10.6 0.25
Class 35 gray cast iron 7.1 241 855 334 110 44 13.0 0.29
Aluminum alloys
2024-T4 2.78 325 470 - 285 73 28.0 23.2 0.33
6061-T6 2.70 275 310 - 205 69 26.0 23.6 0.33
7075-T6 2.80 505 570 - 330 72 26.9 23.6 0.33
Magnesium alloys
AZ80A, as extruded 1.80 250 340 - 150 45 17 26.0 0.35
AZ80A, T5 temper 1.80 275 380 - 165 45 17 26.0 0.35
Copper alloys
C10800 copper, hard-drawn 8.94 220 275 - 180 115 44 17.0 0.33
C26000 cartridge brass, annealed 8.53 110 330 - 235 110 40 19.9 0.38
C26000 cartridge brass, rolled 8.53 360 480 - 290 110 40 19.9 0.38
C63000 aluminum bronze, annealed 7.58 370 766 115 44 16.2 0.33
Titanium alloys
Ti-6Al-4V, annealed 4.43 830 900 - 550 114 42 8.6 0.34
Ti-6Al-4V, heat treated 4.43 1100 1170 - - 114 42 8.6 0.34
Concrete & Stone
Unreinforced concrete (range of
grades)
2.40
0.1× σ
UCS
21 to 28
0.5× σ
UCS
17 to 28 9.9 0.1 to
0.20
Granite (typical) 2.69 170 48 6.5 0.28
Limestone (typical) 2.66 55 to 110 40 5.0 0.21
Sandstone (typical) 2.50 40 17 9.4 0.28
For most metals, the ultimate strength in compression is equal to the ultimate strength in tension.
Concrete, stone, and gray cast iron are significantly stronger in compression than in tension. The elastic portion of their
stress-strain curves are not linear, so Young's modulus is not clearly defined for these materials.
The numbers in these tables are either typical or minimum values, for use in homework problems only. Use standards
published by ASTM, SAE, et al., for materials property values before designing anything.
151

Appendix B: Materials Properties
.$96..0
Bolt Specification
τ
all
τ
all
(ksi) (MPa)
ASTM A307 low-carbon steel 12.0 82.5
ASTM A325N, threads in the shear plane 24.0 165
ASTM A325X, threads excluded from the shear plane 30.0 207
ASTM A490N, threads in the shear plane 30.0 207
ASTM A490X, threads excluded from the shear plane 37.5 260
.%966.0=0
Plate Material
σ
YS
σ
YS
σ
UTS
σ
UTS
σ
P-all
σ
P-all
σ
G-all
σ
G-all
σ
N-all
σ
N-all
(ksi) (MPa) (ksi) (MPa) (ksi) (MPa) (ksi) (MPa) (ksi) (MPa)
ASTM A36 low-
carbon steel
36 250 58 400 87 600 21.6 150 29 200
ASTM A992 high-
strength low-alloy
steel
50 345 65 448 97.5 672 30 207 32.5 224
.&9;-= .'93:=>
Weld Size E60 electrode E70 electrode Plate Thickness Weld Size
(in.) (kip/in.) (kip/in.) (in.) (in.)
1/16 0.795 0.925 1/8 1/8
1/8 1.59 1.85 3/16 1/8 to 3/16
3/16 2.39 2.78 1/4 1/8 to 3/16
1/4 3.18 3.70 5/16 3/16 to 1/4
5/16 3.98 4.63 3/8 3/16 to 5/16
3/8 4.77 5.55 7/16 3/16 to 3/8
7/16 5.57 6.48 1/2 3/16 to 7/16
1/2 6.36 7.40 9/16 1/4 to 1/2
9/16 7.16 8.33 5/8 1/4 to 9/16
5/8 7.95 9.25 11/16 1/4 to 5/8
11/16 8.75 10.18 3/4 1/4 to 11/16
3/4 9.54 11.10 13/16 5/16 to 3/4
13/16 10.34 12.03 7/8 5/16 to 13/16
7/8 11.13 12.95
152

Appendix B: Materials Properties
.(97;
"2
Steels
ASTM A36 Low-carbon, low-strength, low-cost rolled structural steel used for W-beams, I-beams, C-channels, etc.
ASTM A992
(HSLA) &
AISI 80X (HSLA)
High-strength, low-alloy steels contain grain-refining elements such as boron which create very small grains, resulting in higher
strength. Reheating to welding temperatures causes grains to grow, ruining the strength of the steel, therefore bolting or riveting are
preferred. Used for structural steel in buildings and large trucks. By definition, few alloying elements are added, keeping costs low.
AISI 1020 Low-carbon steel containing 0.20% carbon, 0.45% manganese. Cold rolling increases strength & decreases ductility.
AISI 1040 Medium-carbon steel containing 0.40% carbon, 0.75% manganese. Added carbon makes the alloy stronger than AISI 1020. Cold
rolling further increases strength and decreases ductility.
AISI 4140 Add 0.95% chromium, 0.20% molybdenum, and a little manganese to AISI 1040 steel. Cost and strength increase. Quench &
temper heat treatment can raise yield strength above 230 ksi. Used for machine parts.
AISI 8620 Add 0.55% nickel, 0.50% chromium, 0.20% molybdenum, and a little manganese to AISI 1020 steel. Cost and strength increase.
Carburize to make a hard, wear-resistant high-carbon surface for gears and bearings.
Stainless steels
Type 304 Most common stainless steel, with 18% Cr, 8% Ni. Used for food handling equipment (cutlery, pots and pans), tubing, cryogenic
equipment. Hardenable by cold work, but not through heat treatment. Not magnetic.
Type 409, annealed Contains 11% Cr, ½% Ni, therefore cheaper than type 304, with less corrosion resistance. Widely used for stainless exhaust pipes
on cars and trucks. Magnetic.
Cast irons
Grade 4 austempered
ductile iron
Contains 3 to 4% carbon as spherical graphite particles which reduce stress concentrations. Austempering heat treatment gives it
the strength and wear resistance of steel with the low cost and castability of cast iron. Used for crankshafts and other machine parts.
Class 35 gray cast
iron
Contains 2.5 to 4% carbon in the form of graphite flakes which help absorb vibration, but create stress concentrations which reduce
strength. Used for engine blocks and machinery bases. The elastic stress-strain curve is not linear, so yield strength is not reported.
Aluminum alloys
2024-T4 Contains 4.4% copper, 1.5% magnesium, 0.6% manganese. Used widely in the aircraft industry owing to its high strength to weight
ratio. T4 heat treatment quadruples yield strength of the soft annealed condition.
6061-T6 Contains 1% Mg, 0.6% Si, 03% Cu, 0.2% Cr. Used in canoes, trucks, pipelines, and other applications where good strength to
weight ratio, corrosion resistance, and weldability are needed. T6 heat treat raises yield strength 2½ times vs. annealed condition.
7075-T6 Contains 5.6% zinc, 2.5% magnesium, 1.6% copper, 0.23% chromium. Used widely in the aircraft industry owing to its high
strength to weight ratio and corrosion resistance. T6 heat treatment quadruples yield strength.
Magnesium alloys
AZ80A Contains 8.5% aluminum, 0.5% zinc. Commonly used as an extrusion. T5 heat treatment increases strength by 10%.
Copper alloys
C12200 phosphorus
deoxidized copper
Contains min. 99.9% copper. Copper tube used for domestic water, medical gas, air conditioning, and refrigeration. Allowable
stress depends on the amount of cold work, from 6 ksi (annealed) to 10 ksi (as-drawn) at room temp.
C26000 cartridge
brass
Contains 70% Cu, 30% Zn. Cold work and heat treatment substantially improve mechanical properties. Widely used in electrical,
hardware, ammunition, plumbing, and automotive industries. Susceptible to stress-corrosion cracking in the presence of ammonia.
C63000 Al bronze Contains 82% copper, 10% aluminum, 5% nickel, 3% iron. Used for pump parts, valve seats, faucet balls, gears, and cams.
Titanium alloys
Ti-6Al-4V Titanium alloys are expensive to produce partly because molten titanium explodes in air. Ti-6-4 is widely used in aerospace
because it has half the density of steel, but higher strength and stiffness than aluminum aerospace alloys.
Concrete & Stone
Unreinforced
concrete
10 times stronger in compression than in tension; commonly reinforced with steel to improve tensile strength. Wet curing increases
strength as the concrete ages; 90% of strength reached within 28 days of pouring.
Granite Igneous rock. Hard, strong, durable material used for building exteriors and curbstones. Resistant to acid rain.
Limestone Sedimentary rock. Softer than granite, used for building exteriors and gravel for paving. Sensitive to acid rain.
Sandstone Sedimentary rock. Easier to carve than other rock. Used for paving and building exteriors.
10 For more information, consult ASTM Standards, SAE Standards, the ASM Handbook series published by ASM International, the
Copper Tube Handbook, and other engineering handbooks.
153

Appendix C: Properties of Areas
*1&*
6@*@'@06
In these diagrams, the polar moment of inertia, J, is about the center of gravity (the small circle marked
“CG”).
The moments of inertia, I
x
and I
y
, and radii of gyration, r
Gx
and r
Gy
, are about the x-x and y-y neutral axes
(horizontal and vertical magenta lines).
Rectangle Hollow rectangle Circle Hollow circle Thin-walled hollow
circle
̄
x=
b
2
,
̄
y=
h
2
A=b h
I
x
=
bh
3
12
I
y
=
h b
3
12
J =
b h
12
(h
2
+b
2
)
r
Gx
=
h
√
12
r
Gy
=
b
√
12
̄
x=
b
o
2
,
̄
y=
h
o
2
A=b
o
h
o
−b
i
h
i
I
x
=
b
o
h
o
3
−b
i
h
i
3
12
I
y
=
h
o
b
o
3
−h
i
b
i
3
12
J =I
x
+I
y
r
Gx
=
√
b
o
h
o
3
−b
i
h
i
3
12 A
r
Gy
=
√
h
o
b
o
3
−h
i
b
i
3
12 A
̄
x=
̄
y=
d
2
A=
π d
2
4
I
x
=I
y
=
π d
4
64
J =
π d
4
32
r
Gx
=r
Gy
=
d
4
̄
x=
̄
y=
d
o
2
A=
π(d
o
2
−d
i
2
)
4
I
x
=I
y
=
π( d
o
4
−d
i
4
)
64
J =
π (d
o
4
−d
i
4
)
32
r
Gx
=r
Gy
=
√
d
o
2
+d
i
2
4
If a hollow circle has a
thin wall of thickness
t, then the area is
equal to the
circumference times
the wall thickness. The
cross-section of a
copper water pipe is a
good example of a
thin-walled hollow
circle.
d
avg
=
d
o
+d
i
2
̄
x=
̄
y=
d
avg
2
A=π d
avg
t
I
x
=I
y
=
π d
avg
3
t
8
r
Gx
=r
Gy
=
√
d
avg
t
2
154
x x
y
y
CG
b
h
CG
y
x
b
o
h
o
b
i
h
i
CG
y
x
d
CG
y
x
d
o
d
i
CG
y
x
d
avg
CG
t
y
x

Appendix C: Properties of Areas
Ellipse Half circle Quarter circle Segment of a circle 2
nd
degree parabola
A=π a b
I
x
=
πa b
3
4
I
y
=
π b a
3
4
J =
πa b
4
(
a
2
+b
2
)
r
Gx
=
b
2
,
r
Gy
=
a
2
̄
y=
2d
3π
A=
π d
2
8
I
x
=
π d
4
128
[
1−
(
8
3 π
)
2
]
=
d
4
145.78
I
y
=
π d
4
128
,
J =
d
4
31.84
r
Gx
=
d
7.566
,
r
Gy
=
d
4
̄
x=
̄
y=
2d
3π
A=
π d
2
16
I
x
=I
y
=
d
4
291.4
J =
d
4
145.7
r
Gx
=r
Gy
=
d
7.564
̄
x=
d sin θ
3θ
(θ in radians)
A=
θ d
2
4
I
x
=
d
4
(2 θ−sin 2 θ)
128
I
y
=
d
4
(2 θ+sin 2 θ)
128
̄
y=
2h
5
A=
4b h
3
I
x
=0.914 b h
3
I
y
=
4 h b
3
15
Trapezoid, parallel top
and bottom edges
Trapezoid, parallel left
and right edges
Right triangle General triangle Half pipe
̄
y=
h
3
(
2 a+b
a+b
)
A=h
(
a+b
2
)
̄
x=
b
3
(
h
1
+2 h
2
h
1
+h
2
)
A=b
(
h
1
+h
2
2
)
̄
x=
b
3
,
̄
y=
h
3
A=
b h
2
I
x
=
bh
3
36
,
I
y
=
hb
3
36
r
Gx
=
h
√
18
̄
x=
a+b
3
,
̄
y=
h
3
A=
b h
2
I
x
=
b h
3
36
r
Gx
=
h
√
18
̄
y=
2(d
o
3
−d
i
3
)
3π(d
o
2
−d
i
2
)
A=
π
8
(d
o
2
−d
i
2
)
I
x
=
d
o
4
−d
i
4
145.7
−
d
o
2
d
i
2
(d
o
−d
i
)
56.5(d
o
+d
i
)
155
b
CG
a
d
CG
y
d/2
CG
y
x
2b
CG
h
y
b
h
CG
a
y
b
h
2
CG
h
1
x
d/2
CG
θ
x
θ
b
h
y
x
a
CG
b
h
y
x
CG
d
o
CG
y
d
i

Appendix C: Properties of Areas
2
nd
degree half
parabola, vertex at the
top
n
th
degree half
parabola, vertex at the
top
2
nd
degree half
parabola, vertex at the
left
n
th
degree half
parabola, vertex at the
left
̄
x=
3
8
b
,
̄
y=
2
5
h
A=
2
3
bh
̄
x=
b(n+1)
2(n+2)
̄
y=
h n
2n+1
A=
n b h
n+1
̄
x=
b
4
,
̄
y=
3
10
h
A=
1
3
bh
̄
x=
b
n+2
̄
y=h
n+1
4 n+2
A=
b h
n+1
156
b
h
CG
y
x
vertex
b
h
CG
y
x
vertex
b
h
CG
y
x
vertex
b
h
CG
y
x
vertex

Appendix D: Properties of Steel Beams and Pipes
*1 &
(,
Steel is hot-rolled to manufacture beams in shapes that look like the letters I or L. In this diagram, the
flanges are the top and bottom horizontal portions of the beam; the web is the vertical portion. I-
shaped steel beams with wide flanges are called W-beams.
The tables below list geometric properties of hot-rolled steel beams.
U.S. Customary W-beams are designated by the nominal depth and the weight per unit length: a
W18×40 beam has a depth of about 18 inches and a weight per unit length of 40 lb./ft.
7"9;<<=?.
Beam Area Depth Flange
width
Flange
thickness
Web
thickness
Properties with respect to the x-x neutral axis
(moment of inertia, section modulus, radius of
gyration, and plastic section modulus)
Properties with respect to
the y-y neutral axis
w A d b
f
t
f
t
w
I
x
S
x
r
Gx
Z
x
I
y
S
y
r
Gy
(in.)×(lb./ft.) (in.
2
) (in.) (in.) (in.) (in.) (in.
4
) (in.
3
) (in.) (in.
3
) (in.
4
) (in.
3
) (in.)
W44×335 98.5 44.0 15.9 1.77 1.03 31100 1410 17.8 1620 1200 150 3.49
W44×290 85.4 43.6 15.8 1.58 0.865 27000 1240 17.8 1410 1040 132 3.49
W44×262 77.2 43.3 15.8 1.42 0.785 24100 1110 17.7 1270 923 117 3.47
W44×230 67.8 42.9 15.8 1.22 0.710 20800 971 17.5 1100 796 101 3.43
W40×397 117 41.0 16.1 2.20 1.22 32000 1560 16.6 1800 1540 191 3.64
W40×297 87.3 39.8 15.8 1.65 0.930 23200 1170 16.3 1330 1090 138 3.54
W40×199 58.8 38.7 15.8 1.07 0.650 14900 770 16.0 869 695 88.2 3.45
W40×149 43.8 38.2 11.8 0.830 0.630 9800 513 15.0 598 229 38.8 2.29
W36×395 116 38.4 16.8 2.20 1.22 28500 1490 15.7 1710 1750 208 3.88
W36×302 89.0 37.3 16.7 1.68 0.945 21100 1130 15.4 1280 1300 156 3.82
W36×194 57.0 36.5 12.1 1.26 0.765 12100 664 14.6 767 375 61.9 2.56
W36×150 44.3 35.9 12.0 0.940 0.625 9040 504 14.3 581 270 45.1 2.47
W36×135 39.9 35.6 12.0 0.790 0.600 7800 439 14.0 509 225 37.7 2.38
W33×387 114 36.0 16.2 2.28 1.26 24300 1350 14.6 1560 1620 200 3.77
W33×201 59.1 33.7 15.7 1.15 0.715 11600 686 14.0 773 749 95.2 3.56
W33×130 38.3 33.1 11.5 0.855 0.580 6710 406 13.2 467 218 37.9 2.39
W33×118 34.7 32.9 11.5 0.740 0.550 5900 359 13.0 415 187 32.6 2.32
W30×391 115 33.2 15.6 2.44 1.36 20700 1250 13.4 1450 1550 198 3.67
W30×292 86.0 32.0 15.3 1.85 1.02 14900 930 13.2 1060 1100 144 3.58
W30×211 62.3 30.9 15.1 1.32 0.775 10300 665 12.9 751 757 100 3.49
W30×148 43.6 30.7 10.5 1.18 0.650 6680 436 12.4 500 227 43.3 2.28
W30×90 26.3 29.5 10.4 0.610 0.470 3610 245 11.7 283 115 22.1 2.09
W27×368 109 30.4 14.7 2.48 1.38 16200 1060 12.2 1240 1310 179 3.48
W27×281 83.1 29.3 14.4 1.93 1.06 11900 814 12.0 936 953 133 3.39
W27×194 57.1 28.1 14.0 1.34 0.750 7860 559 11.7 631 619 88.1 3.29
W27×146 43.2 27.4 14.0 0.975 0.605 5660 414 11.5 464 443 63.5 3.20
W27×114 33.6 27.3 10.1 0.930 0.570 4080 299 11.0 343 159 31.5 2.18
W27×84 24.7 26.7 10.0 0.640 0.460 2850 213 10.7 244 106 21.2 2.07
W24×370 109 28.0 13.7 2.72 1.52 13400 957 11.1 1130 1160 170 3.27
W24×279 81.9 26.7 13.3 2.09 1.16 9600 718 10.8 835 823 124 3.17
W24×192 56.5 25.5 13.0 1.46 0.810 6260 491 10.5 559 530 81.8 3.07
W24×104 30.7 24.1 12.8 0.750 0.500 3100 258 10.1 289 259 40.7 2.91
W24×76 22.4 23.9 8.99 0.680 0.440 2100 176 9.69 200 82.5 18.4 1.92
W24×55 16.2 23.6 7.01 0.505 0.395 1350 114 9.11 134 29.1 8.30 1.34
W21×201 59.3 23.0 12.6 1.63 0.910 5310 461 9.47 530 542 86.1 3.02
W21×166 48.8 22.5 12.4 1.36 0.750 4280 380 9.36 432 435 70.0 2.99
W21×147 43.2 22.1 12.5 1.15 0.720 3630 329 9.17 373 376 60.1 2.95
W21×83 24.4 21.4 8.36 0.835 0.515 1830 171 8.67 196 81.4 19.5 1.83
W21×62 18.3 21.0 8.24 0.615 0.400 1330 127 8.54 144 57.5 14.0 1.77
W21×50 14.7 20.8 6.53 0.535 0.380 984 94.5 8.18 110 24.9 7.64 1.30
157
t
w
x
d
t
f
b
f
x
y
y
flange
web

Appendix D: Properties of Steel Beams and Pipes
7"9;<<=?.45
Beam Area Depth Flange
width
Flange
thickness
Web
thickness
Properties with respect to the x-x neutral axis
(moment of inertia, section modulus, radius of
gyration, and plastic section modulus)
Properties with respect to
the y-y neutral axis
w A d b
f
t
f
t
w
I
x
S
x
r
Gx
Z
x
I
y
S
y
r
Gy
(in.)×(lb./ft.) (in.
2
) (in.) (in.) (in.) (in.) (in.
4
) (in.
3
) (in.) (in.
3
) (in.
4
) (in.
3
) (in.)
W18×311 91.6 22.3 12.0 2.74 1.52 6970 624 8.72 754 795 132 2.95
W18×211 62.3 20.7 11.6 1.91 1.06 4330 419 8.35 490 493 85.3 2.82
W18×130 38.3 19.3 11.2 1.20 0.670 2460 256 8.03 290 278 49.9 2.70
W18×86 25.3 18.4 11.1 0.770 0.480 1530 166 7.77 186 175 31.6 2.63
W18×60 17.6 18.2 7.56 0.695 0.415 984 108 7.47 123 50.1 13.3 1.68
W18×35 10.3 17.7 6.00 0.425 0.300 510 57.6 7.04 66.5 15.3 5.12 1.22
W16×100 29.4 17.0 10.4 0.985 0.585 1490 175 7.10 198 186 35.7 2.51
W16×67 19.6 16.3 10.2 0.665 0.395 954 117 6.96 130 119 23.2 2.46
W16×40 11.8 16.0 7.00 0.505 0.305 518 64.7 6.63 73.0 28.9 8.25 1.57
W16×31 9.13 15.9 5.53 0.440 0.275 375 47.2 6.41 54.0 12.4 4.49 1.17
W16×26 7.68 15.7 5.50 0.345 0.250 301 38.4 6.26 44.2 9.59 3.49 1.12
W14×159 46.7 15.0 15.6 1.19 0.745 1900 254 6.38 287 748 96.2 4.00
W14×99 29.1 14.2 14.6 0.780 0.485 1110 157 6.17 173 402 55.2 3.71
W14×82 24.0 14.3 10.1 0.855 0.510 881 123 6.05 139 148 29.3 2.48
W14×38 11.2 14.1 6.77 0.515 0.310 385 54.6 5.87 61.5 26.7 7.88 1.55
W14×22 6.49 13.7 5.00 0.335 0.230 199 29.0 5.54 33.2 7.00 2.80 1.04
W12×152 44.7 13.7 12.5 1.40 0.870 1430 209 5.66 243 454 72.8 3.19
W12×106 31.2 12.9 12.2 0.990 0.610 933 145 5.47 164 301 49.3 3.11
W12×72 21.1 12.3 12.0 0.670 0.430 597 97.4 5.31 108 195 32.4 3.04
W12×50 14.6 12.2 8.08 0.640 0.370 391 64.2 5.18 71.9 56.3 13.9 1.96
W12×40 11.7 11.9 8.01 0.515 0.295 307 51.5 5.13 57.0 44.1 11.0 1.94
W12×30 8.79 12.3 6.52 0.440 0.260 238 38.6 5.21 43.1 20.3 6.24 1.52
W12×19 5.57 12.2 4.01 0.350 0.235 130 21.3 4.82 24.7 3.76 1.88 0.822
W12×14 4.16 11.9 3.97 0.225 0.200 88.6 14.9 4.62 17.4 2.36 1.19 0.753
W10×100 29.3 11.1 10.3 1.12 0.680 623 112 4.60 130 207 40.0 2.65
W10×60 17.7 10.2 10.1 0.680 0.420 341 66.7 4.39 74.6 116 23.0 2.57
W10×49 14.4 10.0 10.0 0.560 0.340 272 54.6 4.35 60.4 93.4 18.7 2.54
W10×39 11.5 9.92 7.99 0.530 0.315 209 42.1 4.27 46.8 45.0 11.3 1.98
W10×30 8.84 10.5 5.81 0.510 0.300 170 32.4 4.38 36.6 16.7 5.75 1.37
W10×19 5.62 10.2 4.02 0.395 0.250 96.3 18.8 4.14 21.6 4.29 2.14 0.874
W10×12 3.54 9.87 3.96 0.210 0.190 53.8 10.9 3.90 12.6 2.18 1.10 0.785
W8×67 19.7 9.00 8.28 0.935 0.570 272 60.4 3.72 70.1 88.6 21.4 2.12
W8×40 11.7 8.25 8.07 0.560 0.360 146 35.5 3.53 39.8 49.1 12.2 2.04
W8×31 9.13 8.00 8.00 0.435 0.285 110 27.5 3.47 30.4 37.1 9.27 2.02
W8×24 7.08 7.93 6.50 0.400 0.245 82.7 20.9 3.42 23.1 18.3 5.63 1.61
W8×10 2.96 7.89 3.94 0.205 0.170 30.8 7.81 3.22 8.87 2.09 1.06 0.841
W6×25 7.34 6.38 6.08 0.455 0.320 53.4 16.7 2.70 18.9 17.1 5.61 1.52
W6×15 4.43 5.99 5.99 0.260 0.230 29.1 9.72 2.56 10.8 9.32 3.11 1.45
W6×9 2.68 5.90 3.94 0.215 0.170 16.4 5.56 2.47 6.23 2.20 1.11 0.905
W4×13 3.83 4.16 4.06 0.345 0.280 11.3 5.46 1.72 6.28 3.86 1.90 1.00
158

Appendix D: Properties of Steel Beams and Pipes
W-beams in SI units are designated by the nominal depth and the mass per unit length. See the first part of Chapter 8 for the
method to calculate w, the weight per unit length.
7#93=?.
Beam Area Depth Flange
width
Flange
thickness
Web
thickness
Properties with respect to the x-x neutral axis
(moment of inertia, section modulus, radius of
gyration, and plastic section modulus)
Properties with respect to
the y-y neutral axis
A d b
f
t
f
t
w
I
x
S
x
r
Gx
Z
x
I
y
S
y
r
Gy
(mm)×(kg/m) (mm
2
) (mm) (mm) (mm) (mm) (10
6
mm
4
) (10
3
mm
3
) (mm) (10
3
mm
3
) (10
6
mm
4
) (10
3
mm
3
) (mm)
W1100×499 63500 1120 404 45.0 26.2 12900 23100 452 26500 499 2460 88.6
W1100×433 55100 1110 401 40.1 22.0 11200 20300 452 23100 433 2160 88.6
W1100×390 49800 1100 401 36.1 19.9 10000 18200 450 20800 384 1920 88.1
W1100×343 43700 1090 401 31.0 18.0 8660 15900 445 18000 331 1660 87.1
W1000×591 75500 1040 409 55.9 31.0 13300 25600 422 29500 641 3130 92.5
W1000×443 56300 1010 401 41.9 23.6 9660 19200 414 21800 454 2260 89.9
W1000×296 37900 983 401 27.2 16.5 6200 12600 406 14200 289 1450 87.6
W1000×222 28300 970 300 21.1 16.0 4080 8410 381 9800 95.3 636 58.2
W920×588 74800 975 427 55.9 31.0 11900 24400 399 28000 728 3410 98.6
W920×449 57400 947 424 42.7 24.0 8780 18500 391 21000 541 2560 97.0
W920×289 36800 927 307 32.0 19.4 5040 10900 371 12600 156 1010 65.0
W920×223 28600 912 305 23.9 15.9 3760 8260 363 9520 112 739 62.7
W920×201 25700 904 305 20.1 15.2 3250 7190 356 8340 93.7 618 60.5
W840×576 73500 914 411 57.9 32.0 10100 22100 371 25600 674 3280 95.8
W840×299 38100 856 399 29.2 18.2 4830 11200 356 12700 312 1560 90.4
W840×193 24700 841 292 21.7 14.7 2790 6650 335 7650 90.7 621 60.7
W840×176 22400 836 292 18.8 14.0 2460 5880 330 6800 77.8 534 58.9
W760×582 74200 843 396 62.0 34.5 8620 20500 340 23800 645 3240 93.2
W760×434 55500 813 389 47.0 25.9 6200 15200 335 17400 458 2360 90.9
W760×314 40200 785 384 33.5 19.7 4290 10900 328 12300 315 1640 88.6
W760×220 28100 780 267 30.0 16.5 2780 7140 315 8190 94.5 710 57.9
W760×134 17000 749 264 15.5 11.9 1500 4010 297 4640 47.9 362 53.1
W690×548 70300 772 373 63.0 35.1 6740 17400 310 20300 545 2930 88.4
W690×419 53600 744 366 49.0 26.9 4950 13300 305 15300 397 2180 86.1
W690×289 36800 714 356 34.0 19.1 3270 9160 297 10300 258 1440 83.6
W690×217 27900 696 356 24.8 15.4 2360 6780 292 7600 184 1040 81.3
W690×170 21700 693 257 23.6 14.5 1700 4900 279 5620 66.2 516 55.4
W690×125 15900 678 254 16.3 11.7 1190 3490 272 4000 44.1 347 52.6
W610×551 70300 711 348 69.1 38.6 5580 15700 282 18500 483 2790 83.1
W610×415 52800 678 338 53.1 29.5 4000 11800 274 13700 343 2030 80.5
W610×285 36500 648 330 37.1 20.6 2610 8050 267 9160 221 1340 78.0
W610×155 19800 612 325 19.1 12.7 1290 4230 257 4740 108 667 73.9
W610×113 14500 607 228 17.3 11.2 874 2880 246 3280 34.3 302 48.8
W610×82 10500 599 178 12.8 10.0 562 1870 231 2200 12.1 136 34.0
W530×300 38300 584 320 41.4 23.1 2210 7550 241 8690 226 1410 76.7
W530×248 31500 572 315 34.5 19.1 1780 6230 238 7080 181 1150 75.9
W530×219 27900 561 318 29.2 18.3 1510 5390 233 6110 157 985 74.9
W530×123 15700 544 212 21.2 13.1 762 2800 220 3210 33.9 320 46.5
W530×92 11800 533 209 15.6 10.2 554 2080 217 2360 23.9 229 45.0
W530×74 9480 528 166 13.6 9.65 410 1550 208 1800 10.4 125 33.0
159

Appendix D: Properties of Steel Beams and Pipes
7#93=?.45
Beam Area Depth Flange
width
Flange
thickness
Web
thickness
Properties with respect to the x-x neutral axis
(moment of inertia, section modulus, radius of
gyration, and plastic section modulus)
Properties with respect to
the y-y neutral axis
A d b
f
t
f
t
w
I
x
S
x
r
Gx
Z
x
I
y
S
y
r
Gy
(mm)×(kg/m) (mm
2
) (mm) (mm) (mm) (mm) (10
6
mm
4
) (10
3
mm
3
) (mm) (10
3
mm
3
) (10
6
mm
4
) (10
3
mm
3
) (mm)
W460×464 59100 566 305 69.6 38.6 2900 10200 221 12400 331 2160 74.9
W460×315 40200 526 295 48.5 26.9 1800 6870 212 8030 205 1400 71.6
W460×193 24700 490 284 30.5 17.0 1020 4200 204 4750 116 818 68.6
W460×128 16300 467 282 19.6 12.2 637 2720 197 3050 72.8 518 66.8
W460×89 11400 462 192 17.7 10.5 410 1770 190 2020 20.9 218 42.7
W460×52 6650 450 152 10.8 7.62 212 944 179 1090 6.37 83.9 31.0
W410×149 19000 432 264 25.0 14.9 620 2870 180 3240 77.4 585 63.8
W410×100 12600 414 259 16.9 10.0 397 1920 177 2130 49.5 380 62.5
W410×60 7610 406 178 12.8 7.75 216 1060 168 1200 12.0 135 39.9
W410×46.1 5890 404 140 11.2 6.99 156 773 163 885 5.16 73.6 29.7
W410×38.8 4950 399 140 8.76 6.35 125 629 159 724 3.99 57.2 28.4
W360×237 30100 381 396 30.2 18.9 791 4160 162 4700 311 1580 102
W360×147 18800 361 371 19.8 12.3 462 2570 157 2830 167 905 94.2
W360×122 15500 363 257 21.7 13.0 367 2020 154 2280 61.6 480 63.0
W360×57.8 7230 358 172 13.1 7.87 160 895 149 1010 11.1 129 39.4
W360×32.9 4190 348 127 8.51 5.84 82.8 475 141 544 2.91 45.9 26.4
W310×226 28800 348 318 35.6 22.1 595 3420 144 3980 189 1190 81.0
W310×158 20100 328 310 25.1 15.5 388 2380 139 2690 125 808 79.0
W310×107 13600 312 305 17.0 10.9 248 1600 135 1770 81.2 531 77.2
W310×74 9420 310 205 16.3 9.40 163 1050 132 1180 23.4 228 49.8
W310×60 7550 302 203 13.1 7.49 128 844 130 934 18.4 180 49.3
W310×44.5 5670 312 166 11.2 6.60 99.1 633 132 706 8.45 102 38.6
W310×28.3 3590 310 102 8.89 5.97 54.1 349 122 405 1.57 30.8 20.9
W310×21 2680 302 101 5.72 5.08 36.9 244 117 285 0.982 19.5 19.1
W250×149 18900 282 262 28.4 17.3 259 1840 117 2130 86.2 655 67.3
W250×89 11400 259 257 17.3 10.7 142 1090 112 1220 48.3 377 65.3
W250×73 9290 254 254 14.2 8.64 113 895 110 990 38.9 306 64.5
W250×58 7420 252 203 13.5 8.00 87.0 690 108 767 18.7 185 50.3
W250×44.8 5700 267 148 13.0 7.62 70.8 531 111 600 6.95 94.2 34.8
W250×28.4 3630 259 102 10.0 6.35 40.1 308 105 354 1.79 35.1 22.2
W250×17.9 2280 251 101 5.33 4.83 22.4 179 99.1 206 0.907 18.0 19.9
W200×100 12700 229 210 23.7 14.5 113 990 94.5 1150 36.9 351 53.8
W200×59 7550 210 205 14.2 9.14 60.8 582 89.7 652 20.4 200 51.8
W200×46.1 5890 203 203 11.0 7.24 45.8 451 88.1 498 15.4 152 51.3
W200×35.9 4570 201 165 10.2 6.22 34.4 342 86.9 379 7.62 92.3 40.9
W200×15 1910 200 100 5.21 4.32 12.8 128 81.8 145 0.870 17.4 21.4
W150×37.1 4740 162 154 11.6 8.13 22.2 274 68.6 310 7.12 91.9 38.6
W150×22.5 2860 152 152 6.60 5.84 12.1 159 65.0 177 3.88 51.0 36.8
W150×13.5 1730 150 100 5.46 4.32 6.83 91.1 62.7 102 0.916 18.2 23.0
W100×19.3 2470 106 103 8.76 7.11 4.70 89.5 43.7 103 1.61 31.1 25.4
160

Appendix D: Properties of Steel Beams and Pipes
In the 1920s, iron and steel pipes were available in three thickness grades: Standard Weight, Extra Strong (XS), and Double
Extra Strong (XXS). Subsequently, the “schedule” designation system was developed to cover other pipe wall thicknesses.
Schedule 40 is the same as Standard Weight; Schedule 80 is the same as Extra-Strong. Pipes are available from Schedule 5
to Schedule 160. Regardless of the Schedule, the OD is identical between nominal sizes, so pipes of different Schedules can
thread into the same fittings. The heavier Schedules have thicker walls, therefore smaller IDs.
7$9;6
Nominal
diameter
Inside
diameter
Outside
diameter
Wall
thickness
Area Moment of
inertia
Section
modulus
Radius of
gyration
Polar
moment of
inertia
Weight per
unit length
d
i
d
o
t A I S r
G
J w
(in.) (in.) (in.) (in.) (in.
2
) (in.
4
) (in.
3
) (in.) (in.
4
) (lb./ft.)
Schedule 40
pipes
(Standard
Weight)
1 1.049 1.315 0.133 0.469 0.0830 0.126 0.423 0.166 1.68
2 2.067 2.375 0.154 1.02 0.627 0.528 0.791 1.25 3.66
3 3.068 3.500 0.216 2.07 2.85 1.63 1.17 5.69 7.58
4 4.026 4.500 0.237 2.96 6.82 3.03 1.51 13.6 10.8
5 5.047 5.563 0.258 4.01 14.3 5.14 1.88 28.6 14.6
6 6.065 6.625 0.280 5.20 26.5 7.99 2.25 52.9 19.0
8 7.981 8.625 0.322 7.85 68.1 15.8 2.95 136 28.6
Schedule 80
pipes
(Extra-Strong)
1 0.957 1.315 0.179 0.602 0.101 0.154 0.410 0.202 2.17
2 1.939 2.375 0.218 1.40 0.827 0.696 0.771 1.65 5.03
3 2.900 3.500 0.300 2.83 3.70 2.11 1.14 7.40 10.3
4 3.826 4.500 0.337 4.14 9.12 4.05 1.48 18.2 15.0
5 4.813 5.563 0.375 5.73 19.5 7.02 1.85 39.0 20.8
6 5.761 6.625 0.432 7.83 38.3 11.6 2.20 76.6 28.6
8 7.625 8.625 0.500 11.9 100 23.1 2.89 199 43.4
7%936
Nominal
diameter
Inside
diameter
Outside
diameter
Wall
thickness
Area Moment of
inertia
Section
modulus
Radius of
gyration
Polar
moment of
inertia
Mass per
unit length
d
i
d
o
t A I S r
G
J
(mm) (mm) (mm) (mm) (mm
2
) (10
6
mm
4
) (10
3
mm
3
) (mm) (10
3
mm.
4
) (kg/m)
Schedule 40
pipes
(Standard
Weight)
25 26.7 33.5 3.38 303 0.0345 2.06 10.7 69.1 2.50
51 52.5 60.5 3.91 658 0.261 8.65 20.1 520 5.44
76 78.0 88.9 5.49 1340 1.19 26.7 29.7 2370 11.3
102 102 114 6.02 1910 2.84 49.7 38.4 5660 16.1
127 128 141 6.55 2590 5.95 84.2 47.8 11900 21.7
152 154 168 7.11 3350 11.0 131 57.2 22000 28.3
203 203 219 8.18 5060 28.3 259 74.9 56600 42.5
Schedule 80
pipes
(Extra-Strong)
25 24.3 33.5 4.55 388 0.0420 2.52 10.4 84.1 3.23
51 49.3 60.5 5.54 903 0.344 11.4 19.6 687 7.48
76 73.7 88.9 7.62 1830 1.54 34.6 29.0 3080 15.3
102 97.3 114 8.56 2670 3.80 66.4 37.6 7580 22.3
127 122 141 9.53 3700 8.12 115 47.0 16200 30.9
152 146 168 11.0 5050 15.9 190 55.9 31900 42.5
203 194 219 12.7 7680 41.6 379 73.4 82800 64.5
Additional data on steel beams and pipes are freely available online from the American Institute of Steel Construction
(AISC).
161

Appendix D: Properties of Steel Beams and Pipes
In the 1930s, thin-walled copper tubing was introduced throughout North America for domestic potable water and
baseboard hot water heating. Three types are available in the U.S.:
Type K with the thickest wall, useable for underground applications.
Type L with an intermediate wall thickness, used in interior applications.
Type M with the thinnest wall, used in interior applications (in some areas, legal only for nonpressurized applications
such as condensate drains).
Copper pipes are made with C10800 oxygen-free low-phosphorus copper. The nominal diameter is approximately equal to
the inside diameter. The outside diameters are identical for all Types so they will fit the same elbows, valves, and other
fittings, and are 1/8 of an inch larger than the nominal diameters. Wall thickness
t=
d
o
−d
i
2
.
7&9;<<
Type K Type L Type M All Types
Nominal diameter Inside diameter Inside diameter Inside diameter Outside diameter
d
i
d
i
d
i
d
o
(in.) (in.) (in.) (in.) (in.)
3/8 0.402 0.430 0.450 0.500
1/2 0.528 0.545 0.569 0.625
5/8 0.652 0.668 0.690 0.750
3/4 0.745 0.785 0.811 0.875
1 0.995 1.025 1.055 1.125
1 1/4 1.245 1.265 1.291 1.375
1 1/2 1.481 1.505 1.527 1.625
2 1.959 1.985 2.009 2.125
2 1/2 2.435 2.465 2.495 2.625
3 2.907 2.945 2.981 3.125
Copper water tube sold in SI units comes in Types A, B, and C (similar to Types K, L, and M, above). Nominal diameter is
the outside diameter.
7'93
Type A Type B Type C All Types
Nominal diameter Inside diameter Inside diameter Inside diameter Outside diameter
d
i
d
i
d
i
d
o
(mm) (mm) (mm) (mm) (mm)
10 8.2 8.4 8.8 10
12 9.6 10.2 10.8 12
15 12.6 13.0 13.6 15
18 15.6 16.0 16.6 18
22 18.8 19.8 20.4 22
28 24.8 25.6 26.2 28
35 31.8 32.2 32.8 35
42 38.4 39.0 39.6 42
54 49.8 50.6 51.0 54
67 62.2 63.0 63.8 67
More sizes are available; see ASTM Standards B 88 and B 89 for a complete list.
162

Appendix E: Mechanical and Dimensional Properties of Wood
*1&' (
'*,
Wood is a natural material which varies in mechanical properties. Factors
affecting strength and stiffness include defects (knots, insect and woodpecker
holes), moisture content, service temperature, age of the tree at cutting, direction
within the wood (along the grain, tangential, and radial), and geographic source of
the tree. For example, this graph from the Forest Products Laboratory of the U.S.
Department of Agriculture
*
shows variation in the same visual grade of lumber
(same quality & equivalent species), cut from a wide geographical area.
The Allowable Stress Design method (ASD) sets the design stress at the bottom 5
th
percentile of wood within a stress grade. In theory, 5% of the wood used in any
structure is weaker than the required strength...so use a Factor of Safety to prevent
failure.
"9;<<6
Tree species Allowable Stresses
Bending Horizontal shear Tension
parallel to grain
Compression
parallel to grain
Specific weight Young's modulus
γ E
(psi) (psi) (psi) (psi) (lb./ft.
3
) (ksi)
Eastern white pine 600 135 275 725 22 1100
Southern yellow pine 1400 175 825 1250 34 1700
Hem-fir 1000 150 500 1300 25 1400
Douglas fir 900 180 625 1050 30 1700
Redwood 1000 160 600 1050 25 1300
#936
Tree species Allowable Stresses
Bending Horizontal shear Tension
parallel to grain
Compression
parallel to grain
Density Young's modulus
ρ E
(MPa) (MPa) (MPa) (MPa) (kg/m
3
) (GPa)
Eastern white pine 4.1 0.93 1.9 5.0 350 7.6
Southern yellow pine 9.7 1.2 5.7 8.6 550 11.7
Hem-fir 6.9 1.0 3.4 9.0 400 9.7
Douglas fir 6.2 1.2 4.3 7.2 480 11.7
Redwood 6.9 1.1 4.1 7.2 400 9.0
Additional data on timber are freely available online from the U.S. Forest Products Laboratory of the U.S. Department of
Agriculture at http://www.fpl.fs.fed.us.
* General Technical Report FPL GTR 190, Chapter 7, p. 7-6.
163
1.0 1.8
2.6
Young's modulus, E
(10
6
psi)
0
8
16
Frequency
(%)

Appendix E: Mechanical and Dimensional Properties of Wood
#"8
Softwood is “dressed” or planed from nominal size to the sizes listed below. These sizes are S4S (surfaced four sides).
Weight per unit length depends on the density of the wood. Dried softwoods range in specific weight from 20 to 40 lb./ft.
3
(320 to 640 kg/m
3
). If a 2×4 is made of wood with a specific weight of 30 lb./ft.
3
, its weight per unit length is 1.09 lb./ft.
$9;<<>
Designation Width Depth Area Moment of
inertia
Section
modulus
Weight per unit
length
γ = 20 lb/ft.
3
Weight per unit
length
γ = 30 lb/ft.
3
Weight per unit
length
γ = 40 lb/ft.
3
b d A I
x
S
x
w w w
(in.) (in.) (in.
2
) (in.
4
) (in.
3
) (lb./ft.) (lb./ft.) (lb./ft.)
2×2 1.5 1.5 2.25 0.422 0.563 0.313 0.469 0.625
2×3 1.5 2.5 3.75 1.95 1.56 0.521 0.781 1.04
2×4 1.5 3.5 5.25 5.36 3.06 0.729 1.09 1.46
2×6 1.5 5.5 8.25 20.8 7.56 1.15 1.72 2.29
2×8 1.5 7.25 10.9 47.6 13.1 1.51 2.27 3.02
2×10 1.5 9.25 13.9 98.9 21.4 1.93 2.89 3.85
2×12 1.5 11.25 16.9 178 31.6 2.34 3.52 4.69
4×4 3.5 3.5 12.3 12.5 7.1 1.70 2.55 3.40
4×6 3.5 5.5 19.3 48.5 17.6 2.67 4.01 5.35
4×8 3.5 7.25 25.4 111 30.7 3.52 5.29 7.05
4×10 3.5 9.25 32.4 231 49.9 4.50 6.74 8.99
4×12 3.5 11.25 39.4 415 73.8 5.47 8.20 10.9
4×14 3.5 13.25 46.4 678 102 6.44 9.66 12.9
4×16 3.5 15.25 53.4 1034 136 7.41 11.12 14.8
6×6 5.5 5.5 30.3 76.3 27.7 4.20 6.30 8.40
6×8 5.5 7.5 41.3 193 51.6 5.73 8.59 11.5
6×10 5.5 9.5 52.3 393 82.7 7.26 10.9 14.5
6×12 5.5 11.5 63.3 697 121 8.78 13.2 17.6
6×14 5.5 13.5 74.3 1130 167 10.3 15.5 20.6
6×16 5.5 15.5 85.3 1710 220 11.8 17.8 23.7
6×18 5.5 17.5 96.3 2460 281 13.4 20.1 26.7
6×20 5.5 19.5 107 3400 349 14.9 22.3 29.8
8×8 7.5 7.5 56.3 264 70.3 7.81 11.7 15.6
8×10 7.5 9.5 71.3 536 113 9.90 14.8 19.8
8×12 7.5 11.5 86.3 951 165 12.0 18.0 24.0
8×14 7.5 13.5 101 1540 228 14.1 21.1 28.1
8×16 7.5 15.5 116 2330 300 16.1 24.2 32.3
8×18 7.5 17.5 131 3350 383 18.2 27.3 36.5
8×20 7.5 19.5 146 4630 475 20.3 30.5 40.6
10×10 9.5 9.5 90.3 679 143 12.5 18.8 25.1
10×12 9.5 11.5 109 1200 209 15.2 22.8 30.3
10×14 9.5 13.5 128 1950 289 17.8 26.7 35.6
10×16 9.5 15.5 147 2950 380 20.5 30.7 40.9
10×18 9.5 17.5 166 4240 485 23.1 34.6 46.2
10×20 9.5 19.5 185 5870 602 25.7 38.6 51.5
10×22 9.5 21.5 204 7870 732 28.4 42.6 56.7
10×24 9.5 23.5 223 10300 874 31.0 46.5 62.0
12×12 11.5 11.5 132 1460 253 18.4 27.6 36.7
12×14 11.5 13.5 155 2360 349 21.6 32.3 43.1
12×16 11.5 15.5 178 3570 460 24.8 37.1 49.5
12×18 11.5 17.5 201 5140 587 28.0 41.9 55.9
12×20 11.5 19.5 224 7110 729 31.1 46.7 62.3
12×22 11.5 21.5 247 9520 886 34.3 51.5 68.7
12×24 11.5 23.5 270 12400 1060 37.5 56.3 75.1
164

Appendix E: Mechanical and Dimensional Properties of Wood
Timber beams in SI units are listed by their mass per unit length, not by their weight per unit length. A 200×360 timber
beam made of wood with a density of 320 kg/m
3
has a mass per unit length of 21 kg/m. Multiply by the mass per unit length
by gravity to obtain weight per unit length:
21 kg
m
9.81 m
s
2
∣
N s
2
kg m
=206 N /m
.
%93>
Designation Width Depth Area Moment of
inertia
Section
modulus
Mass per unit
length
ρ = 320 kg/m
3
Mass per unit
length
ρ = 480 kg/m
3
Mass per unit
length
ρ = 640 kg/m
3
b d A I
x
S
x
m/L m/L m/L
(mm) (mm) (10
3
mm
2
) (10
6
mm
4
) (10
3
mm
3
) (kg/m) (kg/m) (kg/m)
50×100 38.1 88.9 3.39 2.23 50.2 1.09 1.63 2.17
50×150 38.1 140 5.33 8.71 124 1.71 2.56 3.42
50×200 38.1 184 7.01 19.8 215 2.25 3.37 4.49
50×250 38.1 235 8.95 41.2 351 2.87 4.30 5.74
50×300 38.1 286 10.9 74.3 519 3.49 5.24 6.98
50×360 38.1 337 12.8 122 721 4.12 6.17 8.23
50×410 38.1 387 14.7 184 951 4.73 7.09 9.45
100×100 88.9 88.9 7.90 5.21 117 2.53 3.80 5.07
100×150 88.9 140 12.4 20.3 290 3.99 5.98 7.98
100×200 88.9 184 16.4 46.2 502 5.24 7.86 10.5
100×250 88.9 235 20.9 96.1 818 6.70 10.0 13.4
100×300 88.9 286 25.4 173 1212 8.15 12.2 16.3
100×360 88.9 337 30.0 284 1683 9.60 14.4 19.2
100×410 88.9 388 34.5 433 2230 11.1 16.6 22.1
150×150 140 140 19.6 32.0 457 6.28 9.42 12.6
150×200 140 191 26.7 81.3 851 8.57 12.9 17.1
150×250 140 241 33.7 163 1360 10.8 16.2 21.6
150×300 140 292 40.9 290 1990 13.1 19.7 26.2
150×360 140 343 48.0 471 2750 15.4 23.1 30.8
150×410 140 394 55.2 714 3620 17.7 26.5 35.4
150×460 140 445 62.3 1030 4620 20.0 30.0 39.9
150×510 140 496 69.4 1420 5740 22.3 33.4 44.5
200×200 191 191 36.5 111 1160 11.7 17.5 23.4
200×250 191 241 46.0 223 1850 14.8 22.1 29.5
200×300 191 292 55.8 396 2710 17.9 26.8 35.7
200×360 191 343 65.5 642 3750 21.0 31.5 42.0
200×410 191 394 75.3 974 4940 24.1 36.2 48.2
200×460 191 445 85.0 1400 6300 27.2 40.9 54.5
200×510 191 496 94.7 1940 7830 30.4 45.5 60.7
250×250 241 241 58.1 281 2330 18.6 27.9 37.2
250×300 241 292 70.4 500 3420 22.6 33.8 45.1
250×360 241 343 82.7 810 4730 26.5 39.7 53.0
250×410 241 394 95.0 1230 6240 30.4 45.7 60.9
250×460 241 445 107 1770 7950 34.4 51.6 68.7
250×510 241 495 119 2440 9840 38.2 57.4 76.5
250×560 241 546 132 3270 12000 42.2 63.3 84.3
250×610 241 597 144 4270 14300 46.1 69.2 92.2
300×300 292 292 85 606 4150 27.3 41.0 54.7
300×360 292 343 100 982 5730 32.1 48.2 64.2
300×410 292 394 115 1490 7550 36.9 55.3 73.7
300×460 292 445 130 2140 9640 41.6 62.5 83.3
300×510 292 495 145 2950 11900 46.3 69.5 92.7
300×560 292 546 159 3960 14500 51.1 76.7 102
300×610 292 597 174 5180 17300 55.9 83.8 112
165

Appendix F: Beam Equations
*1+&F
;.,
R
A
and R
B
are the reaction forces at points A and B. M
B
is the reaction moment at point B.
V
x
, M
x
and Δ
x
are the shear load, bending moment, and deflection at a distance x from the left end of the beam.
M
a
and Δ
a
are the bending moment and deflection at a distance x = a from the left end of the beam.
Every beam in this Appendix has a length L.
6?
R
A
=R
B
=V
max
=
P
2
M
max
=
P L
4
at the point load
M
x
=
P x
2
for
x<
L
2
Δ
max
=
P L
3
48 E I
at the point load
Δ
x
=
P x
48 E I
(3 L
2
−4 x
2
)
for
x≤
L
2
6?
R
A
=
P b
L
,
R
B
=
P a
L
, V
max
is the greater of the two
M
max
=
P a b
L
at the point load
M
x
=
P b x
L
for x < a
Δ
max
=
P a b(a +2b)
√
3 a(a+2 b)
27 E I L
at
x=
√
a(a +2 b)
3
when a > b
Δ
a
=
P a
2
b
2
3E I L
at the point load
Δ
x
=
P b x
6 E I L
(L
2
−b
2
−x
2
)
for x < a
166
P
A B
R
A
V
R
A
R
B
L/2 L/2
R
B
M
M
max
Elastic
curve
x
Δ
max
P
A B
R
A
V
R
A
R
B
a b
R
B
M
M
max
Elastic
curve
x
Δ
max

Appendix F: Beam Equations
?
R
A
=R
B
=V
max
=P
M
max
=P a
between the point loads
M
x
=P x
for x < a
Δ
max
=
P a
24 E I
(3 L
2
−4 a
2
)
at the midspan
Δ
x
=
P x
6 E I
(3 L a−3a
2
−x
2
)
for
x≤a
Δ
x
=
P a
6 E I
(3 L x−3 x
2
−a
2
)
between the point loads
;
?
R
A
=R
B
=V
max
=
w L
2
V
x
=w
(
L
2
−x
)
M
max
=
w L
2
8
at the midspan
M
x
=
w x
2
(L−x)
Δ
max
=
5w L
4
384 E I
at the midspan
Δ
x
=
w x
24 E I
(L
3
−2 L x
2
+x
3
)
;?
R
A
=V
max
=
w a
2 L
(2 L−a )
,
R
B
=
w a
2
2 L
V
x
=R
A
−w x
for
x≤a
;
V
x
=−R
B
for
x≥a
M
max
=
R
A
2
2w
at
x=
R
A
w
M
x
=R
A
x−
w x
2
2
for
x≤a
;
M
x
=R
B
(L−x)
for
x≥a
Δ
x
=
w x
24 E I L
[
a
2
(2 L−a )
2
−2 a x
2
(2 L−a)+L x
3
]
for
x≤a
Δ
x
=
w a
2
(L−x)
24 E I L
(4 x L−2 x
2
−a
2
)
for
x≥a
167
P
A B
R
A
V
R
A
R
B
a a
R
B
M
M
max
Elastic
curve
x
Δ
max
P
L/2
A B
R
A
V
R
B
w
b
M
max
M
Elastic
curve
Δ
max
x
a
A B
R
A
V
R
B
w
L
M
max
M
Elastic
curve
Δ
max
x

Appendix F: Beam Equations
/
R
A
=
w
max
L
6
,
R
B
=
w
max
L
3
V
x
=
w
max
L
6
−
w
max
x
2
2 L
M
max
=
w
max
L
2
9
√
3
at
x=
L
√
3
M
x
=
w
max
L x
6 L
2
(L
2
−x
2
)
Δ
max
=0.00652
w
max
L
4
E I
at
x= L
√
1−
√
8
15
Δ
x
=
w
max
x
360 E I L
(3 x
4
−10 L
2
x
2
+7 L
4
)
/?
R
A
=R
B
=V
max
=
w
max
L
4
V
x
=
w
max
4 L
(L
2
−4 x
2
)
for
x<
L
2
M
max
=
w
max
L
2
12
at the midspan
M
x
=
w
max
L x
2
(
1
2
−
2 x
2
3 L
2
)
for
x<
L
2
Δ
max
=
w
max
L
4
120 E I
at the midspan
Δ
x
=
w
max
x
960 E I L
(
5 L
2
−4 x
2
)
2
for
x<
L
2
6@
R
B
=V
max
=P
M
B
=M
max
=P L
M
x
=P x
Δ
max
=
P L
3
3 E I
at the free end
Δ
x
=
P
6 E I
(2L
3
−3 L
2
x+ x
3
)
168
A B
R
A
V
R
B
w
max
L
M
max
M
Elastic
curve
Δ
max
x
A B
R
A
V
R
B
w
max
L
M
max
M
Elastic
curve
Δ
max
x
P
A B
V
R
B
L
R
B
M
M
max
Elastic
curve
x
Δ
max
M
B

Appendix F: Beam Equations
6@
R
B
=V
max
=P
M
B
=M
max
=P b
M
x
=P (x−a )
for x > a
Δ
max
=
P b
2
6 E I
(3 L−b)
at the free end
Δ
a
=
P b
3
3E I
at the point load
Δ
x
=
P b
2
6 E I
(3 L−3 x−b)
for x < a
Δ
x
=
P ( L− x)
2
6 E I
(3 b−L+ x)
for x > a
The beam bends in an arc between the support and the point load. To the
left of the point load, the beam is straight, but at an angle.
;
@
R
B
=V
max
=wL
V
x
=w x
M
B
=M
max
=
w L
2
2
M
x
=
w x
2
2
Δ
max
=
w L
4
8E I
at the free end
Δ
x
=
w
24 E I
(x
4
−4 L
3
x+3 L
4
)
169
P
A B
V
R
B
b
R
B
M
M
max
Elastic
curve
x
Δ
max
M
B
a
Δ
a
straight
segment
curved segment
A B
V
R
B
L
R
B
M
M
max
Elastic
curve
x
Δ
max
M
B
w

Appendix F: Beam Equations
/
@
R
B
=V
max
=
w
max
L
2
V
x
=
w
max
x
2
2 L
M
B
=M
max
=
w
max
L
2
6
M
x
=
w
max
x
3
6 L
Δ
max
=
w
max
L
4
30 E I
at the free end
Δ
x
=
w
max
120 E I L
(x
5
−5 L
4
x+4 L
5
)
170
A B
V
R
B
L
R
B
M
M
max
Elastic
curve
x
Δ
max
M
B
w
max
Index
1
3
Allowable moment in a beam.........................................................83
Allowable stress in welded tanks....................................................29
Angle of twist in a round shaft.......................................................57
Average web shear approach..........................................................89
Beam deflection...............................................................................94
Beam design, steel.........................................................................102
Beam design, wood...............................................................108, 110
Beam reactions................................................................................60
Bending moment diagrams.............................................................72
Bending stress in beams..................................................................82
Bending stress in steel beams.........................................................84
Bolted joints....................................................................................33
Buckling of columns.....................................................................124
Cantilever beams.............................................................................60
Centroid ..........................................................................................41
Centroidal axis.................................................................................41
Column buckling...........................................................................124
Columns, ideal slender..................................................................124
Columns, steel...............................................................................126
Columns, steel machine parts.......................................................127
Columns, support conditions........................................................125
Combined stresses.........................................................................112
Deflection diagrams........................................................................82
Eccentric loading...........................................................................114
Effective length of a column.........................................................125
Efficiency, bolted & welded joints.................................................36
Elastic deformation.........................................................................18
Elastic modulus...............................................................................18
Equivalent load diagram.................................................................63
Euler critical load..........................................................................124
Euler stress....................................................................................125
Factor-label method of unit conversion..........................................12
Failure theories..............................................................................145
Flexure formula...............................................................................82
Formula method of beam analysis..................................................95
Hollow shafts...................................................................................56
Hoop stress......................................................................................28
Ideal slender columns....................................................................124
Interpolation..................................................................................108
Isostress lines.................................................................................131
Joint efficiency in bolted & welded joints......................................36
Load diagrams.................................................................................61
Longitudinal stress in a pipe...........................................................29
Microstrain......................................................................................17
Modulus of elasticity.......................................................................18
Modulus, shear................................................................................55
Mohr's circle..................................................................................131
Moment diagrams............................................................................72
Moment of inertia............................................................................41
Neutral axis......................................................................................82
Overhanging beams.........................................................................64
Pipes.................................................................................................28
Plastic deformation..........................................................................18
Plastic moment................................................................................85
Plastic section modulus...................................................................85
Poisson's ratio..................................................................................23
Polar moment of inertia..................................................................54
Pressure vessels...............................................................................28
Radius of curvature of a beam........................................................94
Radius of gyration...........................................................................54
Reference axis.................................................................................45
Rupture strength..............................................................................18
S4S.................................................................................................164
Section modulus..............................................................................83
Shafts in torsion...............................................................................55
Shear diagrams................................................................................66
Shear stress......................................................................................20
Shear stress in beams......................................................................87
Shear stress in round shafts.............................................................55
Short block....................................................................................115
Simply-supported beams.................................................................60
Statically indeterminate beams.....................................................118
Steel beam design..........................................................................102
Steel columns................................................................................126
Steel machine part columns..........................................................127
Strain................................................................................................17
Stress concentration in tension.......................................................30
Stress concentration in torsion........................................................58
Stress-strain curve...........................................................................17
Stress, tensile...................................................................................17
Stress, thermal.................................................................................26
Superposition..................................................................98, 112, 118
Tensile strength...............................................................................18
Terminology......................................................................................6
Thermal expansion..........................................................................25
Thin-walled pipe.............................................................................28
Timber beam design..............................................................108, 110
Torsion in round shafts...................................................................55
Transfer formula..............................................................................44
Ultimate tensile strength.................................................................18
Unit systems & conversions......................................................149p.
Visualizing Stress and Strain........................................................130
Welded lap joints.............................................................................38
Wood beam design................................................................108, 110
Yield strength..................................................................................18
Young's modulus.............................................................................18
171
